Professor of Computer Science and Mathematics
Chair,
Computer Science Department
Courant Institute of Mathematical Sciences
Contact Info:
New York University
60 5th Ave, 5th floor
New York, NY 10011
Phone: +1 (212) 998-3405
Email (administrative matters): cs-chair@cs.nyu.edu
Email: dzorin@cs.nyu.edu
Research Interests
Geometric modeling: subdivision surfaces, variational modeling, manifold constructions, interactive and appearance based modeling, discretization of geometric quantities.
Scientific computing: Fast multipole methods, numerical solution of integral equations, fluid and deformable membrane simulation, parallel algorithms and software tools.
Publications
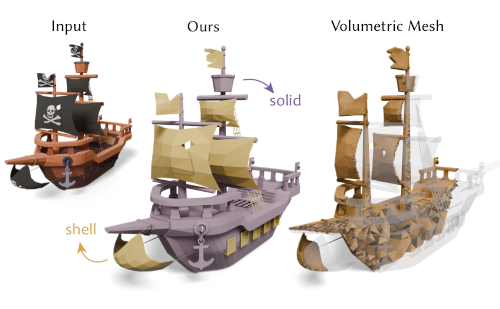 Solid-Shell Labeling for Discrete Surfaces
Solid-Shell Labeling for Discrete Surfaces
Siqi Wang,
Janos Meny,
Izak Grguric,
Mehdi Rahimzadeh,
Denis Zorin,
Daniele Panozzo,
Hsueh-Ti Derek Liu,
SIGGRAPH Asia , 2025
Artist-created meshes in-the-wild often do not have a well defined interior. We observe that they typically consist of a mix of solid elements, faces that bound a volume, and shell elements that represent the medial surface of a thin shell. The lack of a well-defined interior prevents downstream applications, such as solid-modeling, simulation, and manufacturing. We present a method that takes as input a surface mesh and assigns to each face a label determining whether it belongs to a solid or shell. These labels reduce ambiguity by defining the interior for solid faces through thresholding the generalized winding number field, and for shell faces as the volume within an offset. We cast the labeling problem as an optimization that outputs a solid/shell label for each face, guided by a sparse set of user inputs. Once labeling is complete, we show how the shape can be volume meshed by passing the shell faces through an offset mesher and the solid faces to an off-the-shelf tetrahedral mesher, producing a final volumetric mesh by taking their union. Experiments on diverse meshes with defects and multiple solid and shell components demonstrate that our approach delivers the desired labels, enabling modeling and simulation on wild meshes in a way that respects the user intent.
[
Paper]
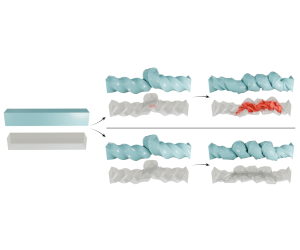 High-Order Continuous Geometrical Validity
High-Order Continuous Geometrical Validity
Federico Sichetti,
Zizhou Huang,
Marco Attene,
Denis Zorin,
Enrico Puppo,
Daniele Panozzo,
ACM Transaction on Graphics , 2025
We propose a conservative algorithm to test the geometrical validity of simplicial (triangles, tetrahedra), tensor product (quadrilaterals, hexahedra), and mixed (prisms) elements of arbitrary polynomial order as they deform linearly within a time interval. Our algorithm uses a combination of adaptive Bézier refinement and bisection search to determine if, when, and where the Jacobian determinant of an elementâs polynomial geometric map becomes negative in the transition from one configuration to another. In elastodynamic simulation, our algorithm guarantees that the system remains physically valid during the entire trajectory, not only at discrete time steps. Unlike previous approaches, physical validity is preserved even when our method is implemented using floating point arithmetic. Hence, our algorithm is only slightly slower than existing non-conservative methods while providing guarantees and while being an easy drop-in replacement for current validity tests. To prove the practical effectiveness of our algorithm, we demonstrate its use in a high-order Incremental Potential Contact (IPC) elastodynamic simulator and experimentally show that it prevents invalid, simulationbreaking configurations that would otherwise occur using non-conservative methods.
[
Paper]
[
Code]
 Feature-Aligned Parametrization in Penner Coordinates
Feature-Aligned Parametrization in Penner Coordinates
Ryan Capouellez,
Rodrigo Singh,
Martin Heistermann,
David Bommes,
Denis Zorin,
ACM Transaction on Graphics (SIGGRAPH) , 2025
Parametrization is a key element of many geometric modeling tasks. Seamless parametrization, in particular, is needed as a starting point for many algorithms for quadrangulation and conversion to high-order patches, as well as for the construction of seamless texture maps and displacement maps. Seamless parametrizations are difficult to compute robustly, in part because, in general, it is not known if one exists for a given mesh connectivity or for a particular configuration of singularities. Recently, Penner-coordinatebased methods that allow for connectivity changes have been shown to achieve a perfect success rate on a widely used dataset (Thingi10k). However, previously proposed Penner coordinate methods do not support sharp feature alignment or soft alignment with preferred directions on the surface, both of which are important for practical applications, especially those involving models with sharp features. In this paper, we extend Penner coordinates to surfaces with sharp features to which the parametrization needs to be aligned. Our algorithm extends the holonomy signature description of seamless parametrizations to surfaces with marked feature curves. We describe sufficient conditions for obtaining feasible solutions and describe a two-phase method to efficiently enforce feature constraints or minimize residual errors when solutions are unattainable. We demonstrate that the resulting algorithm works robustly on the Thingi10k dataset with automatic feature labeling, and the resulting seamless parametrizations can be optimized, quantized, and quadrangulated, completing the quad mesh generation pipeline.
[
Paper]
[
Website]
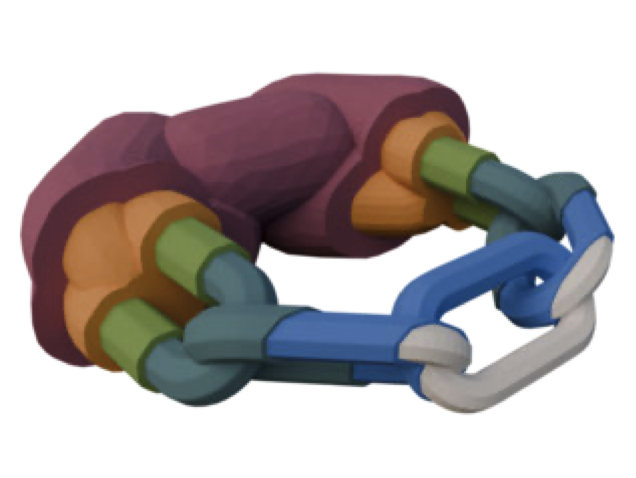 Topological Offsets
Topological Offsets
Daniel Zint,
Zhouyuan Chen,
Yifei Zhu,
Denis Zorin,
Teseo Schneider,
Daniele Panozzo,
ACM Transaction on Graphics (SIGGRAPH) , 2025
We introduce Topological Offsets, a novel approach to generate manifold and self-intersection-free offset surfaces that are topologically equivalent to an offset infinitesimally close to the surface. Our approach, by construction, creates a manifold, watertight, and self-intersection-free offset surface strictly enclosing the input, while doing a best effort to move it to a prescribed distance from the input. Differently from existing approaches, we embed the input in a background mesh and insert a topological offset around the input with purely combinatorial operations. The topological offset is then inflated/deflated to match the user-prescribed distance while enforcing that no intersections or non-manifold configurations are introduced. We evaluate the effectiveness and robustness of our approach on the Thingi10k dataset, and show that topological offsets are beneficial in multiple graphics applications, including (1) converting non-manifold surfaces to manifold ones, (2) creating layered offsets, and (3) reliably computing finite offsets.
[
Paper]
[
Code]
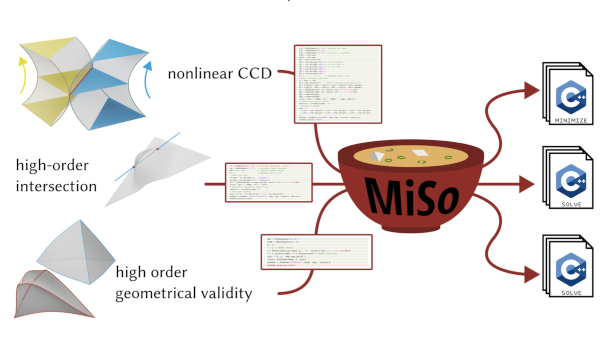 MiSo: A DSL for Robust and Efficient Solve and Minimize Problems
MiSo: A DSL for Robust and Efficient Solve and Minimize Problems
Federico Sichetti,
Enrico Puppo,
Zizhou Huang,
Marco Attene,
Denis Zorin,
Daniele Panozzo,
ACM Transaction on Graphics (SIGGRAPH) , 2025
Many problems in computer graphics can be formulated as finding the global minimum of a function subject to a set of non-linear constraints (Minimize), or finding all solutions of a system of non-linear constraints (Solve). We introduce MiSo, a domain-specific language and compiler for generating efficient C++ code for low-dimensional Minimize and Solve problems, that uses interval methods to guarantee conservative results while using floating point arithmetic. We demonstrate that MiSo-generated code shows competitive performance compared to hand-optimized codes for several computer graphics problems, including high-order collision detection with non-linear trajectories, surface-surface intersection, and geometrical validity checks for finite element simulation.
[
Paper]
[
Code]
 Intersection-Free Garment Retargeting
Intersection-Free Garment Retargeting
Zizhou Huang,
Chrystiano Araujo,
Andrew Junz,
Denis Zorin,
Daniele Panozzo,
Victor Zordan,
SIGGRAPH , 2025
Manual design of garments for avatars requires a large eï¬ort. Garment retargeting methods can save manual eï¬orts by automatically deforming an existing garment design from one avatar to another. Previous methods are limited to human avatars with small variations in body shapes, while non-human avatars with unrealistic characteristics widely appear in games and animations. In this paper, the goal is to retarget artist-designed garments on a standard mannequin to a more general class of avatars. While there is a lack of training data of various avatars wearing garments, we propose a training-free method that performs optimizations on the mesh representation of the garments, with a combination of loss functions that preserve the geometrical features in the original design, guarantee intersection-free, and ï¬t the garment adaptively to the avatars. Our method produces simulationready garment models that can be used later in avatar animations.
[
Paper]
[
Video]
[
Supplemental]
[
Code]
[
Website]
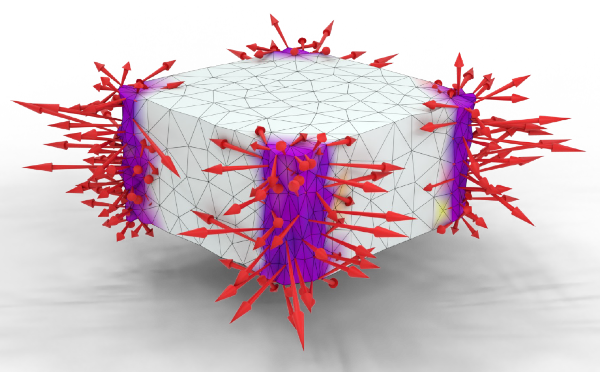 Geometric Contact Potential
Geometric Contact Potential
Zizhou Huang,
Maxwell Paik,
Zachary Ferguson,
Daniele Panozzo,
Denis Zorin,
ACM Transaction on Graphics (SIGGRAPH) , 2025
Barrier potentials gained popularity as a means for robust contact handling in physical modeling and for modeling self-avoiding shapes. The key to the success of these approaches is adherence to geometric constraints, i.e., avoiding intersections, which are the cause of most robustness problems in complex deformation simulation with contact. However, existing barrierpotential methods may lead to spurious forces and imperfect satisfaction of the geometric constraints. They may have strong resolution dependence, requiring careful adaptation of the potential parameters to the object discretizations. We present a systematic derivation of a continuum potential deï¬ned for smooth and piecewise smooth surfaces, starting from identifying a set of natural requirements for contact potentials, including the barrier property, locality, diï¬erentiable dependence on shape, and absence of forces in rest conï¬gurations. Our potential is formulated independently of surface discretization and addresses the shortcomings of existing potential-based methods while retaining their advantages. We present a discretization of our potential that is a drop-in replacement for the potential used in the incremental potential contact formulation [Li et al. 2020], and compare its behavior to other potential formulations, demonstrating that it has the expected behavior. The presented formulation connects existing barrier approaches, as all recent existing methods can be viewed as a variation of the presented potential, and lays a foundation for developing alternative (e.g., higher-order) versions.
[
Paper]
[
Video]
[
Supplemental]
[
Code]
[
Website]
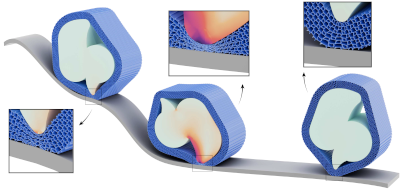 Optimized shock-protecting microstructures
Optimized shock-protecting microstructures
Zizhou Huang,
Daniele Panozzo,
Denis Zorin,
ACM Transaction on Graphics (SIGGRAPH Asia) , 2024
Mechanical shock is a common occurrence in various settings, there are two diï¬erent scenarios for shock protection: catastrophic protection (e.g. car collisions and falls) and routine protection (e.g. shoe soles and mattresses). The former protects against one-time events, the latter against periodic shocks and loads. Common shock absorbers based on plasticity and fracturing materials are suitable for the former, while our focus is on the latter, where elastic structures are useful. Further, we optimize the eï¬ective elastic material properties which control the critical shock parameter, maximal stress, with energy dissipation by viscous forces assumed adequate. Improved elastic materials protecting against shock can be used in applications such as automotive suspension, furniture like sofas and mattresses, landing gear systems, etc. Materials oï¬ering optimal protection against shock have a highly non-linear elastic response: their reaction force needs to be as close as possible to constant with respect to deformation. In this paper, we use shape optimization and topology search to design 2D families of microstructures approximating the ideal behavior across a range of deformations, leading to superior shock protection. We present an algorithmic pipeline for the optimal design of such families combining differentiable nonlinear homogenization with self-contact and an optimization algorithm. We validate the eï¬ectiveness of our advanced 2D designs by extruding and fabricating them with 3D printing technologies and performing material and drop testing.
[
Paper]
[
Video]
[
Code]
 Cut-Cell Microstructures for Two-scale Structural Optimization
Cut-Cell Microstructures for Two-scale Structural Optimization
Davi Colli Tozoni,
Zizhou Huang,
Daniele Panozzo,
Denis Zorin,
SGP , 2024
Two-scale topology optimization, combined with the design of microstructure families with a broad range of effective material parameters, is widely used in many fabrication applications to achieve a target deformation behavior for a variety of objects. The main idea of this approach is to optimize the distribution of material properties in the object partitioned into relatively coarse cells, and then replace each cell with microstructure geometry that mimics these material properties. In this paper, we focus on adapting this approach to complex shapes in situations when preserving the shape's surface is essential. Our approach extends any regular (i.e. defined on a regular lattice grid) microstructure family to complex shapes, by enriching it with tiles adapted to the geometry of the cut-cell. We propose a fully automated and robust pipeline based on this approach, and we show that the performance of the regular microstructure family is only minimally affected by our extension while allowing its use on 2D and 3D shapes of high complexity.
[
Paper]
[
Code]
 Soft Pneumatic Actuator Design using Differentiable Simulation
Soft Pneumatic Actuator Design using Differentiable Simulation
Arvi Gjoka,
Espen Knoop,
Moritz Bacher,
Denis Zorin,
Daniele Panozzo,
Siggraph , 2024
We propose a computational design pipeline for pneumaticallyactuated soft robots interacting with their environment through contact. We optimize the shape of the robot with a shape optimization approach, using a physically-accurate high-order finite element model for the forward simulation. Our approach enables fine-grained control over both deformation and contact forces by optimizing the shape of internal cavities, which we exploit to design pneumatically-actuated robots that can assume user-prescribed poses, or apply user-controlled forces. We demonstrate the efficacy of our method on two artistic and two functional examples.
[
Paper]
[
Video]
[
Supplemental Material]
[
Code]
 Differentiable solver for time-dependent deformation problems with contact
Differentiable solver for time-dependent deformation problems with contact
Zizhou Huang,
Davi Colli Tozoni,
Arvi Gjoka,
Zachary Ferguson,
Teseo Schneider,
Daniele Panozzo,
Denis Zorin,
ACM Transaction on Graphics , 2024
We introduce a general differentiable solver for time-dependent deformation problems with contact and friction. Our approach uses a finite element discretization with a high-order time integrator coupled with the recently proposed incremental potential contact method for handling contact and friction forces to solve ODE- and PDE-constrained optimization problems on scenes with complex geometry. It supports static and dynamic problems and differentiation with respect to all physical parameters involved in the physical problem description, which include shape, material parameters, friction parameters, and initial conditions. Our analytically derived adjoint formulation is efficient, with a small overhead (typically less than 10\% for nonlinear problems) over the forward simulation, and shares many similarities with the forward problem, allowing the reuse of large parts of existing forward simulator code. We implement our approach on top of the open-source PolyFEM library and demonstrate the applicability of our solver to shape design, initial condition optimization, and material estimation on both simulated results and physical validations.
[
Paper]
[
Video]
[
Code]
[
Data]
 Algebraic Smooth Occluding Contours
Algebraic Smooth Occluding Contours
Ryan Capouellez,
Jiacheng Dai,
Aaron Hertzmann,
Denis Zorin,
ACM Transaction on Graphics (SIGGRAPH Asia) , 2023
Computing occluding contours is a key step in 3D non-photorealistic rendering, but producing smooth contours with consistent visibility has been a notoriously-challenging open problem. This paper describes the first general-purpose smooth surface construction for which the occluding contours can be computed in closed form. Given an input mesh and camera viewpoint, we show how to approximate the mesh with a piecewise-quadratic surface, for which the occluding contours are piecewise-rational curves in image-space. We show that this method produces smooth contours with consistent visibility much more efficiently than the state-of-the-art.
[
Paper]
[
Video]
[
Code]
[
Project]
 Bezier Spline Simplification Using Locally Integrated Error Metrics
Bezier Spline Simplification Using Locally Integrated Error Metrics
Siqi Wang,
Chenxi Liu,
Daniele Panozzo,
Denis Zorin,
Alec Jacobson,
SIGGRAPH Asia , 2023
Inspired by surface mesh simplification methods, we present a technique for reducing the number of Bezier curves in a vector graphics while maintaining high fidelity. We propose a curve-to- curve distance metric to repeatedly conduct local segment removal operations. By construction, we identify all possible lossless removal operations ensuring the smallest possible zero-error representation of a given design. Subsequent lossy operations are computed via local Gauss-Newton optimization and processed in a priority queue. We tested our method on the OpenClipArts dataset of 20,000 real- world vector graphics images and show significant improvements over representative previous methods. The generality of our method allows us to show results for curves with varying thickness and for vector graphics animations.
[
Paper]
[
Video]
 High-Order Incremental Potential Contact for Elastodynamic Simulation on Curved Meshes
High-Order Incremental Potential Contact for Elastodynamic Simulation on Curved Meshes
Zachary Ferguson,
Pranav Jain,
Denis Zorin,
Teseo Schneider,
Daniele Panozzo,
SIGGRAPH , 2023
We extend the Incremental Potential Contact method to high-order finite element basis and curved meshes. We do so by coupling together a high-order volumetric representation with a linear surface representation. This provides improved accuracy while maintaining efficient collision detection and response, leading to significant improvements in running times.
[
Paper]
[
Video]
[
Code]
[
Data]
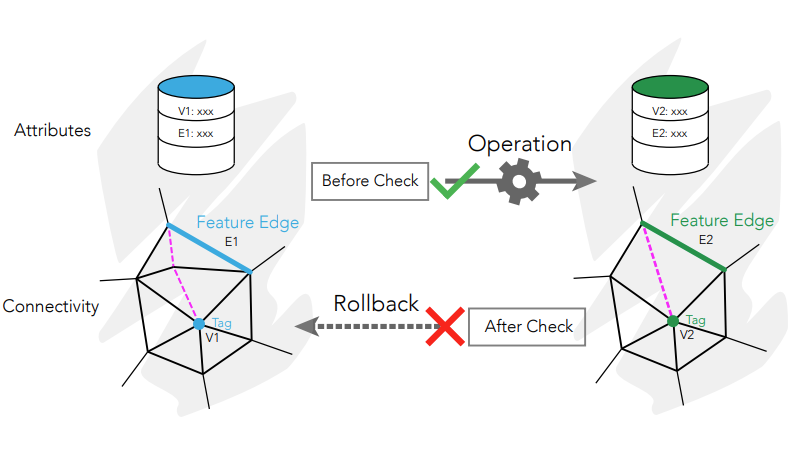 Declarative Specification for Unstructured Mesh Editing Algorithms
Declarative Specification for Unstructured Mesh Editing Algorithms
Zhongshi Jiang,
Jiacheng Dai,
Yixin Hu,
YunFan Zhou,
Jeremie Dumas,
Qingnan Zhou,
Gurkirat Singh Bajwa,
Denis Zorin,
Daniele Panozzo,
Teseo Schneider,
ACM Transaction on Graphics (SIGGRAPH Asia) , 2022
We introduce a novel approach to describe mesh generation, mesh adaptation, and geometric modeling algorithms relying on changing mesh connectivity using a high-level abstraction. The main motivation is to enable easy customization and development of these algorithms via a declarative specification consisting of a set of per-element invariants, operation scheduling, and attribute transfer for each editing operation. We demonstrate that widely used algorithms editing surfaces and volumes can be compactly expressed with our abstraction, and their implementation within our framework is simple, automatically parallelizable on shared memory architectures, and with guaranteed satisfaction of the prescribed invariants. These algorithms are readable and easy to customize for specific use cases.
[
Paper]
[
Code]
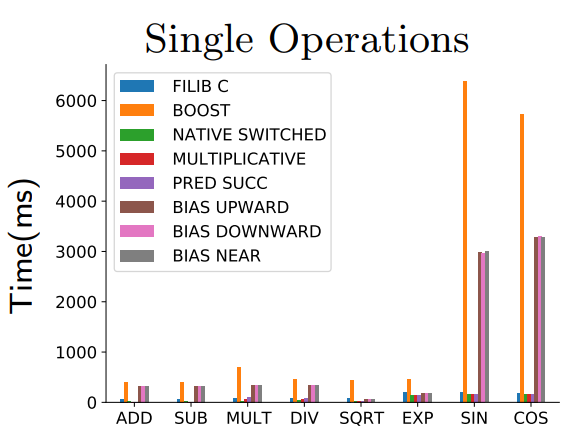 A Cross-Platform Benchmark for Interval Computation Libraries
A Cross-Platform Benchmark for Interval Computation Libraries
Xuan Tang,
Zachary Ferguson,
Teseo Schneider,
Denis Zorin,
Shoaib Kamil,
Daniele Panozzo,
PPAM , 2022
Interval computation is widely used in Computer Aided Design to certify computations that use floating point operations to avoid pitfalls related to rounding error introduced by inaccurate operations. Despite its popularity and practical benefits, support for interval arithmetic is not standardized nor available in mainstream programming languages. We propose the first benchmark for interval computations, coupled with reference solutions computed with exact arithmetic, and compare popular C and C++ libraries over different architectures, operating systems, and compilers. The benchmark allows identifying limitations in existing implementations, and provides a reliable guide on which library to use on each system for different CAD applications. We believe that our benchmark will be useful for developers of future interval libraries, as a way to test the correctness and performance of their algorithms.
[
Paper]
[
Code]
 Which Cross Fields can be Quadrangulated? Global Parameterization from Prescribed Holonomy Signatures
Which Cross Fields can be Quadrangulated? Global Parameterization from Prescribed Holonomy Signatures
Hanxiao Shen,
Leyi Zhu,
Ryan Capouellez,
Daniele Panozzo,
Marcel Campen,
Denis Zorin,
Transactions on Graphics (SIGGRAPH) , 2022
We describe a method for the generation of seamless surface parametrizations with guaranteed local injectivity and full control over holonomy. Previous methods guarantee only one of the two. Local injectivity is required to enable these parametrizationsâ use in applications such as surface quadrangulation and spline construction. Holonomy control is crucial to enable guidance or prescription of the parametrizationâs isocurves based on directional information, in particular from cross-fields or feature curves, and more generally to constrain the parametrization topologically. To this end we investigate the relation between cross-field topology and seamless parametrization topology. Leveraging previous results on locally injective parametrization and combining them with insights on this relation in terms of holonomy, we propose an algorithm that meets these requirements. A key component relies on the insight that arbitrary surface cut graphs, as required for global parametrization, can be homeomorphically modified to assume almost any set of turning numbers with respect to a given target cross-field
[
Paper]
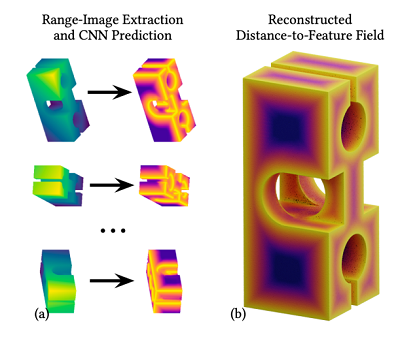 DEF: Deep Estimation of Sharp Geometric Features in 3D Shapes
DEF: Deep Estimation of Sharp Geometric Features in 3D Shapes
Albert Matveev,
Ruslan Rakhimov,
Alexey Artemov,
Gleb Bobrovskikh,
Vage Egiazarian,
Emil Bogomolov,
Daniele Panozzo,
Denis Zorin,
Evgeny Burnaev,
Transactions on Graphics (SIGGRAPH) , 2022
We propose Deep Estimators of Features (DEFs), a learning-based framework for predicting sharp geometric features in sampled 3D shapes. Differently from existing data-driven methods, which reduce this problem to feature classification, we propose to regress a scalar field representing the distance from point samples to the closest feature line on local patches. Our approach is the first that scales to massive point clouds by fusing distance-to-feature estimates obtained on individual patches.We extensively evaluate our approach against related state-of-the-art methods on newly proposed synthetic and real-world 3D CAD model benchmarks. Our approach not only outperforms these (with improvements in Recall and False Positives Rates), but generalizes to real-world scans after training our model on synthetic data and fine-tuning it on a small dataset of scanned data. We demonstrate a downstream application, where we reconstruct an explicit representation of straight and curved sharp feature lines from range scan data.
[
Paper]
[
Code/Data]
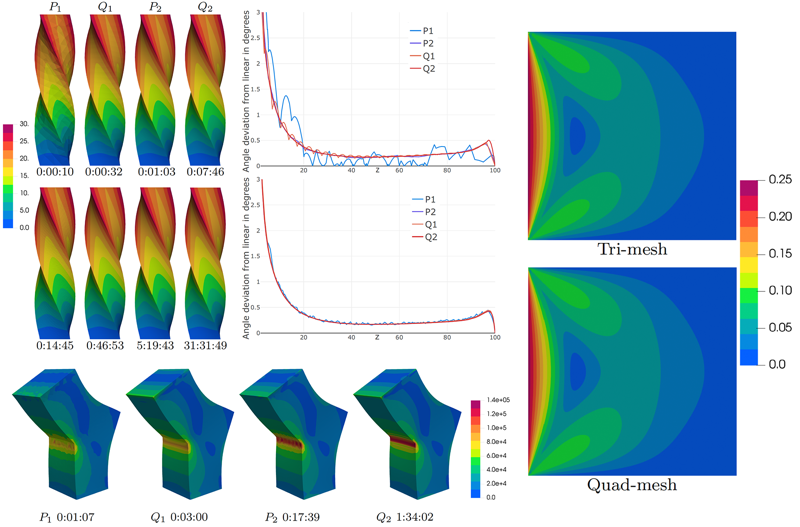 A Large Scale Comparison of Tetrahedral and Hexahedral Elements for Finite Element Analysis
A Large Scale Comparison of Tetrahedral and Hexahedral Elements for Finite Element Analysis
Teseo Schneider,
Yixin Hu,
Xifeng Gao,
Jeremie Dumas,
Denis Zorin,
Daniele Panozzo,
Transaction on Graphics , 2022
The Finite Element Method (FEM) is widely used to solve discrete Partial Differential Equations (PDEs) in engineering and graphics applications. The popularity of FEM led to the development of a large family of variants, most of which require a tetrahedral or hexahedral mesh to construct the basis. While the theoretical properties of FEM basis (such as convergence rate, stability, etc.) are well understood under specific assumptions on the mesh quality, their practical performance, influenced \emph{both} by the choice of the basis construction and quality of mesh generation, have not been systematically documented for large collections of automatically meshed 3D geometries. We introduce a set of benchmark problems involving most commonly solved \revisionn{elliptic} PDEs, starting from simple cases with an analytical solution, moving to commonly used test problem setups, and using manufactured solutions for thousands of real-world, automatically meshed geometries. For all these cases, we use state-of-the-art meshing tools to create both tetrahedral and hexahedral meshes, and compare the performance of different element types for common elliptic PDEs. The goal of his benchmark is to enable comparison of complete FEM pipelines, from mesh generation to algebraic solver, and exploration of relative impact of different factors on the overall system performance. As a specific application of our geometry and benchmark dataset, we explore the question of relative advantages of unstructured (triangular/tetrahedral) and structured (quadrilateral/hexahedral) discretizations. We observe that for Lagrange-type elements, while linear tetrahedral elements perform poorly, quadratic tetrahedral elements perform equally well or outperform hexahedral elements for our set of problems and currently available mesh generation algorithms. This observation suggests that for common problems in structural analysis, thermal analysis, and low Reynolds number flows, high-quality results can be obtained with unstructured tetrahedral meshes, which can be created robustly and automatically. We release the description of the benchmark problems, meshes, and reference implementation of our testing infrastructure to enable statistically significant comparisons between different FE methods, which we hope will be helpful in the development of new meshing and FEA techniques.
[
Paper]
[
Code]
[
Data]
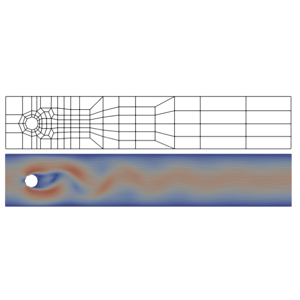 A Large-Scale Benchmark for the Incompressible Navier-Stokes Equations
A Large-Scale Benchmark for the Incompressible Navier-Stokes Equations
Zizhou Huang,
Teseo Schneider,
Minchen Li,
Chenfanfu Jiang,
Denis Zorin,
Daniele Panozzo,
Arxiv , 2021
Numerical methods for solving incompressible Navier-Stokes equations are widely applied and are among the most extensively studied. A plethora of approaches have been introduced targeting different applications and regimes; these methods vary in space discretization, choice of time integration scheme, or reduction of the non-linear equations to a sequence of simpler problems. While the theoretical properties of most of these variants are known, it is still difficult to pick the best option for a given problem, as practical performance of these methods has never been systematically compared over a varied set of geometries and boundary conditions. We introduce a collection of benchmark problems in 2D and 3D (geometry description and boundary conditions), including simple cases with known analytic solution, classical experimental setups, and complex geometries with fabricated solutions for evaluation of numerical schemes for incompressible Navier-Stokes equations in laminar flow regime. We compare the performance of a representative selection of most broadly used algorithms for Navier-Stokes equations on this set of problems. Where applicable, we compare the most common spatial discretization choices (un- structured triangle/tetrahedral meshes and structured or semi-structured quadrilateral/hexahedral meshes). The study shows that while the type of spatial discretization used has a minor impact on the accuracy of the solutions, the choice of time integration method, spatial discretization order, and the choice of solving the coupled equations or reducing them to simpler subproblems have very different properties. Methods that are directly solving the original equations tend to be more accurate than splitting approaches for the same number of degrees of freedom, but numerical or computational difficulty arise when they are scaled to larger problem sizes. Low-order splitting methods are less accurate, but scale more easily to large problems, while higher-order splitting methods are accurate but require dense time discretizations to be stable. We release the description of the experiments and an implementation of our benchmark, which we believe will enable statistically significant comparisons with the state of the art as new approaches for solving the incompressible Navier-Stokes equations are introduced.
[
Paper]
[
Website]
 Hardware Design and Accurate Simulation for Benchmarking of 3D Reconstruction Algorithms
Hardware Design and Accurate Simulation for Benchmarking of 3D Reconstruction Algorithms
Sebastian Koch,
Yurii Piadyk,
Markus Worchel,
Marc Alexa,
Claudio T. Silva,
Denis Zorin,
Daniele Panozzo,
Neural Information Processing Systems (NeurIPS 2021) Track on Datasets and Benchmarks , 2021
We co-develop a 3D structured light scanning hardware setup together with a corresponding light transport simulation with the objective of minimizing the difference of per-pixel values. For diffusely reflecting objects we show that differences between the real image taken by the camera and the synthesized image are negligible. This provides an ideal test-bed for developing data-driven algorithms in the area of 3D reconstruction, as the synthetic data is indistinguishable from real data. Pixel-wise matching also provides an effective way to evaluate data-driven reconstruction algorithms objectively. We introduce three benchmark problems using the data generated with our system: (1) a benchmark for surface reconstruction from dense point clouds, (2) a denoising procedure tailored to structured light scanning, and (3) a range scan completion algorithm for CAD models, trained on the ABC CAD dataset. We also provide a large collection of high-resolution scans that allow our system and benchmarks to be used without having to reproduce the hardware setup.
[
Paper]
[
Website]
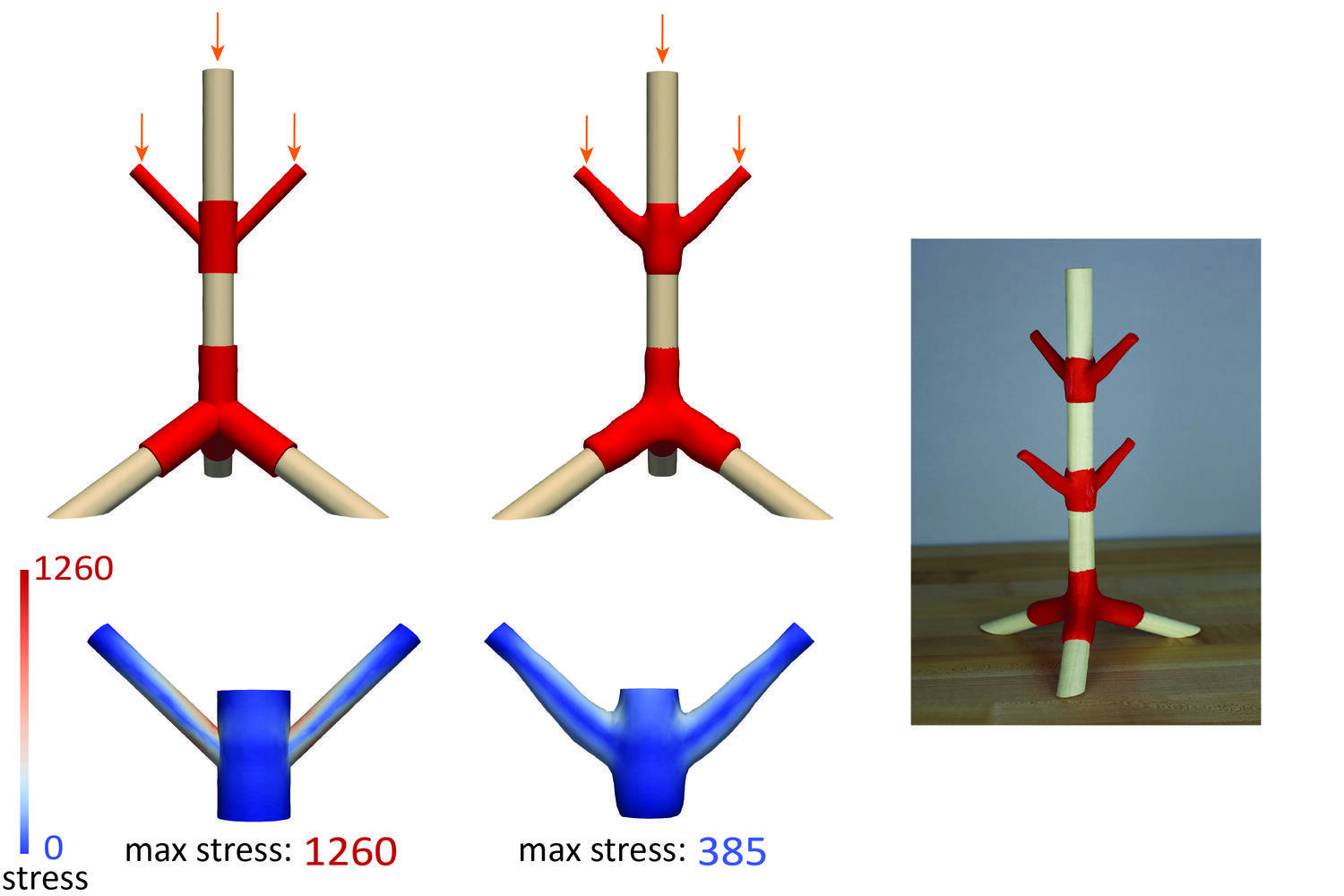 Optimizing Contact-based Assemblies
Optimizing Contact-based Assemblies
Davi Colli Tozoni,
YunFan Zhou,
Denis Zorin,
ACM Transaction on Graphics (SIGGRAPH Asia) , 2021
Modern fabrication methods have greatly simplified manufacturing of complex free-form shapes at an affordable cost, and opened up new possibilities for improving functionality and customization through automatic optimization, shape optimization in particular. However, most existing shape optimization methods focus on single parts. In this work, we focus on supporting shape optimization for assemblies, more specifically, assemblies that are held together by contact and friction. Examples of which include furniture joints, construction set assemblies, certain types of prosthetic devices and many other. To enable this optimization, we present a framework supporting robust and accurate optimization of a number of important functionals, while enforcing constraints essential for assembly functionality: weight, stress, difficulty of putting the assembly together, and how reliably it stays together. Our framework is based on smoothed formulation of elasticity equations with contact, analytically derived shape derivatives, and robust remeshing to enable large changes of shape, and at the same time, maintain accuracy. We demonstrate the improvements it can achieve for a number of computational and experimental examples.
[
Paper]
[
Supplemental]
[
Supplemental Video]
 Efficient and Robust Discrete Conformal Equivalence with Boundary
Efficient and Robust Discrete Conformal Equivalence with Boundary
Marcel Campen,
Ryan Capouellez,
Hanxiao Shen,
Leyi Zhu,
Daniele Panozzo,
Denis Zorin,
ACM Transaction on Graphics (SIGGRAPH Asia) , 2021
We describe an efficient algorithm to compute a discrete metric with prescribed Gaussian curvature at all interior vertices and prescribed geodesic curvature along the boundary of a mesh. The metric is (discretely) conformally equivalent to the input metric. Its construction is based on theory developed in [Gu et al. 2018b] and [Springborn 2020], relying on results on hyperbolic ideal Delaunay triangulations. Generality is achieved by considering the surfaceâs intrinsic triangulation as a degree of freedom, and particular attention is paid to the proper treatment of surface boundaries. While via a double cover approach the case with boundary can be reduced to the case without boundary quite naturally, the implied symmetry of the setting causes additional challenges related to stable Delaunay-critical configurations that we address explicitly. We furthermore explore the numerical limits of the approach and derive continuous maps from the discrete metrics.
[
Paper]
[
Code]
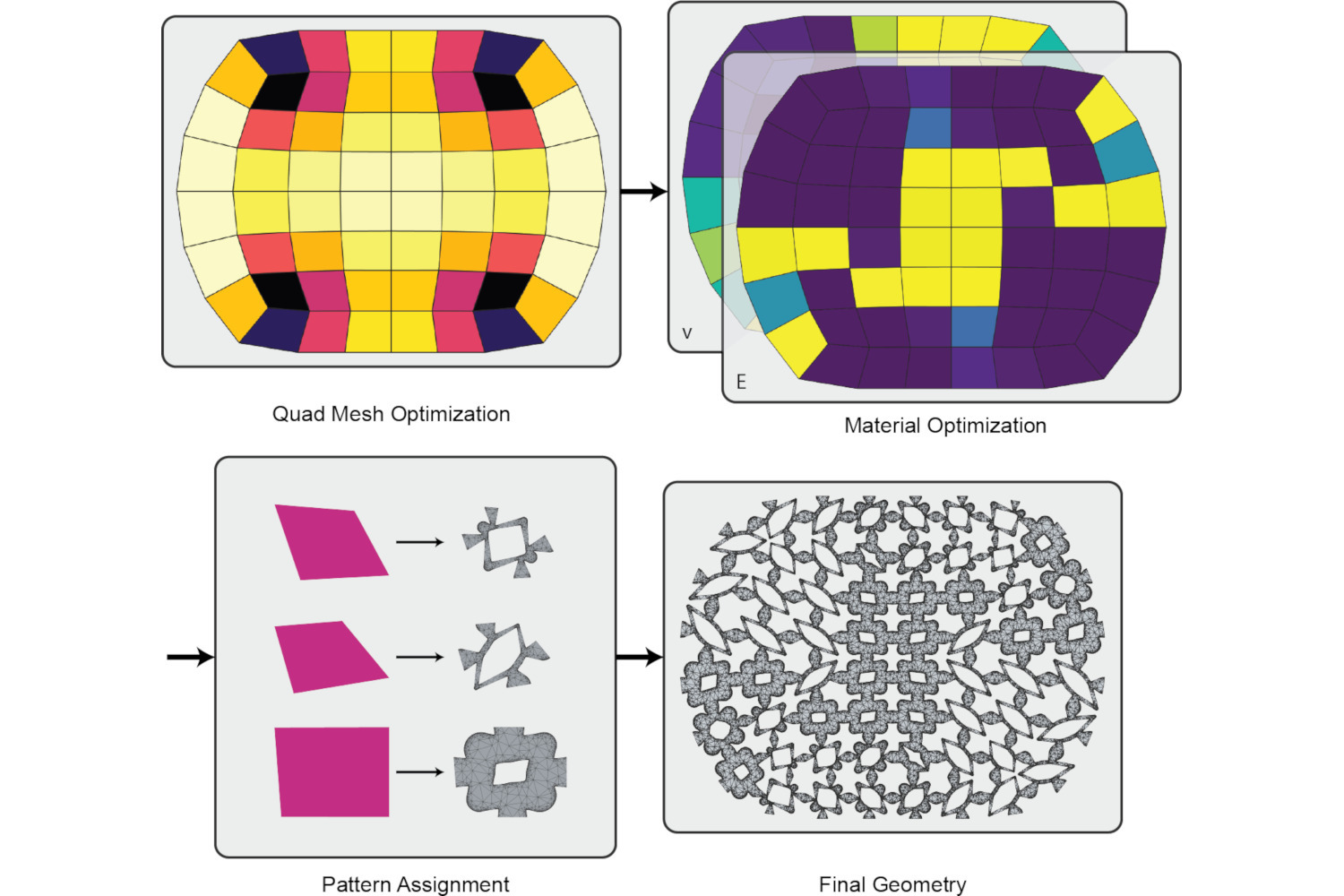
 An Extensible Benchmark Suite for Learning to Simulate Physical Systems
An Extensible Benchmark Suite for Learning to Simulate Physical Systems
Karl Otness,
Arvi Gjoka,
Joan Bruna,
Daniele Panozzo,
Benjamin Peherstorfer,
Teseo Schneider,
Denis Zorin,
Neural Information Processing Systems (NeurIPS 2021) Track on Datasets and Benchmarks , 2021
Simulating physical systems is a core component of scientific computing, encompassing a wide range of physical domains and applications. Recently, there has been a surge in data-driven methods to complement traditional numerical simulations methods, motivated by the opportunity to reduce computational costs and/or learn new physical models leveraging access to large collections of data. However, the diversity of problem settings and applications has led to a plethora of approaches, each one evaluated on a different setup and with different evaluation metrics. We introduce a set of benchmark problems to take a step towards unified benchmarks and evaluation protocols. We propose four representative physical systems, as well as a collection of both widely used classical time integrators and representative data-driven methods (kernel-based, MLP, CNN, Nearest-Neighbors). Our frame12 work allows to evaluate objectively and systematically the stability, accuracy, and computational efficiency of data-driven methods. Additionally, it is configurable to permit adjustments for accommodating other learning tasks and for establishing a foundation for future developments in machine learning for scientific computing.
[
Paper]
[
Code]
[
Data]
 Intersection-free Rigid Body Dynamics
Intersection-free Rigid Body Dynamics
Zachary Ferguson,
Minchen Li,
Teseo Schneider,
Francisca Gil Ureta,
Timothy Langlois,
Chenfanfu Jiang,
Denis Zorin,
Danny M. Kaufman,
Daniele Panozzo,
ACM Transaction on Graphics (SIGGRAPH) , 2021
We introduce the first implicit time-stepping algorithm for rigid body dynamics, with contact and friction, that guarantees intersection-free configurations at every time step. Our algorithm explicitly models the curved trajectories traced by rigid bodies in both collision detection and response. For collision detection, we propose a conservative narrow phase collision detection algorithm for curved trajectories, which reduces the problem to a sequence of linear CCD queries with minimal separation. For time integration and contact response, we extend the recently proposed incremental potential contact framework to reduced coordinates and rigid body dynamics. We introduce a benchmark for rigid body simulation and show that our approach, while less efficient than alternatives, can robustly handle a wide array of complex scenes, which cannot be simulated with competing methods, without requiring per-scene parameter tuning.
[
Paper]
[
Video 1]
[
Video 2]
[
Website]
 Bijective and Coarse High-Order Tetrahedral Meshes
Bijective and Coarse High-Order Tetrahedral Meshes
Zhongshi Jiang,
Ziyi Zhang,
Yixin Hu,
Teseo Schneider,
Denis Zorin,
Daniele Panozzo,
ACM Transaction on Graphics (SIGGRAPH) , 2021
A robust and automatic approach to convert triangle meshes to coarse high order tetrahedral meshes. ideal for p-FEM simulations. We equip the final and intermediate results with a bijective operator, to bound geometric error, maintain consistent fitting, and preserve features precisely. The map reliably linking input and output boundary can be used to transfer attributes and solutions.
[
Paper]
[
Code]
 Orienting Point Clouds With Dipole Propagation
Orienting Point Clouds With Dipole Propagation
Gal Metzer,
Rana Hanocka,
Denis Zorin,
Raja Giryes,
Daniele Panozzo,
Daniel Cohen-Or,
ACM Transaction on Graphics (SIGGRAPH) , 2021
Establishing a consistent normal orientation for point clouds is a notoriously difficult problem in geometry processing, requiring attention to both local and global shape characteristics. The normal direction of a point is a function of the local surface neighborhood; yet, point clouds do not disclose the full underlying surface structure. Even assuming known geodesic proximity, calculating a consistent normal orientation requires the global context. In this work, we introduce a novel approach for establishing a globally consistent normal orientation for point clouds. Our solution separates the local and global components into two different sub-problems. In the local phase, we train a neural network to learn a coherent normal direction per patch (i.e., consistently oriented normals within a single patch). In the global phase, we propagate the orientation across all coherent patches using a dipole propagation. Our dipole propagation decides to orient each patch using the electric field defined by all previously orientated patches. This gives rise to a global propagation that is stable, as well as being robust to nearby surfaces, holes, sharp features and noise.
[
Paper]
[
Video]
[
Website]
 Appearance-Preserving Tactile Optimization
Appearance-Preserving Tactile Optimization
Chelsea Tymms,
Siqi Wang,
Denis Zorin,
ACM Transaction on Graphics (SIGGRAPH Asia) , 2020
Textures are encountered often on various common objects and surfaces. Many textures combine visual and tactile aspects, each serving important purposes; most obviously, a texture alters the objectâs appearance or tactile feeling as well as serving for visual or tactile identification and improving usability. The tactile feel and visual appearance of objects are often linked, but they may interact in unpredictable ways. Advances in high-resolution 3D printing enable highly flexible control of geometry to permit manipulation of both visual appearance and tactile properties. In this paper, we propose an optimization method to independently control the tactile properties and visual appearance of a texture. Our optimization is enabled by neural network-based models, and allows the creation of textures with a desired tactile feeling while preserving a desired visual appearance at a relatively low computational cost, for use in a variety of applications.
[
Paper]
[
Supplemental Material]
[
Code]
 Bijective Projection in a Shell
Bijective Projection in a Shell
Zhongshi Jiang,
Teseo Schneider,
Denis Zorin,
Daniele Panozzo,
ACM Transaction on Graphics (SIGGRAPH Asia) , 2020
We introduce an algorithm to convert a self-intersection free, orientable, and manifold triangle mesh T into a generalized prismatic shell equipped with a bijective projection operator to map T to a class of discrete surface contained within the shell whose normals satisfy a simple local condition. Properties can be robustly and eï¬ciently transferred between these surfaces using the prismatic layer as a common parametrization domain. The combination of the prismatic shell construction and corresponding projection operator is a robust building block readily usable in many downstream applications, including the solution of PDEs, displacement maps synthesis, Boolean operations, tetrahedral meshing, geometric textures, and nested cages.
[
Paper]
[
Code]
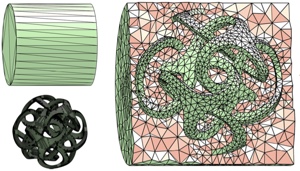
 A Low-Parametric Rhombic Microstructure Family for Irregular Lattices
A Low-Parametric Rhombic Microstructure Family for Irregular Lattices
Davi Colli Tozoni,
Jeremie Dumas,
Zhongshi Jiang,
Julian Panetta,
Daniele Panozzo,
Denis Zorin,
ACM Transaction on Graphics (SIGGRAPH) , 2020
New fabrication technologies have significantly decreased the cost of fabrication of shapes with highly complex geometric structure. One important application of complex fine-scale geometric structures is to create variable effective elastic material properties in shapes manufactured from a single material. Modification of material properties has a variety of uses, from aerospace applications to soft robotics and prosthetic devices. Due to its scalability and effectiveness, an increasingly common approach to creating spatially varying materials is to partition a shape into cells and use a parametric family of small-scale geometric structures with known effective properties to fill the cells. We propose a new approach to solving this problem for extruded, planar microstructures. Differently from existing methods for two-scale optimization based on regular grids with square periodic cells, which cannot conform to an arbitrary boundary, we introduce cell decompositions consisting of (nearly) rhombic cells. These meshes have far greater flexibility than those with square cells in terms of approximating arbitrary shapes, and, at the same time, have a number of properties simplifying small-scale structure construction. Our main contributions include a new family of 2D cell geometry structures, explicitly parameterized by their effective Youngâs moduli ð¸, Poissonâs ratios ð, and rhombic angle ð¼ with the geometry parameters expressed directly as smooth spline functions of ð¸, ð, and ð¼. This family leads to smooth transitions between the tiles and can handle a broad range of rhombic cell shapes. We introduce a complete material design pipeline based on this microstructure family, composed of an algorithm to generate rhombic tessellation from quadrilateral meshes and an algorithm to synthesize the microstructure geometry. We fabricated a number of models and experimentally demonstrated how our method, in combination with material optimization, can be used to achieve the desired deformation behavior.
[
Paper]
[
Code]
[
Supplemental]
[
Talk]
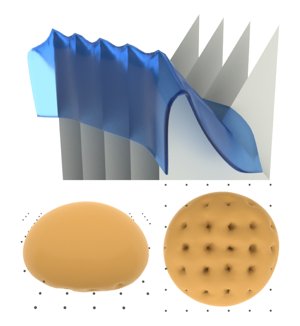
 Fast Tetrahedral Meshing in the Wild
Fast Tetrahedral Meshing in the Wild
Yixin Hu,
Teseo Schneider,
Bolun Wang,
Denis Zorin,
Daniele Panozzo,
ACM Transaction on Graphics (SIGGRAPH) , 2020
We propose a new tetrahedral meshing method, fTetWild, to convert triangle soups into high-quality tetrahedral meshes. Our method builds on the TetWild algorithm, replacing the rational triangle insertion with a new incremental approach to construct and optimize the output mesh, interleaving triangle insertion and mesh optimization. Our approach makes it possible to maintain a valid floating-point tetrahedral mesh at all algorithmic stages, eliminating the need for costly constructions with rational numbers used by TetWild, while maintaining full robustness and similar output quality. This allows us to improve on TetWild in two ways. First, our algorithm is significantly faster, with running time comparable to less robust Delaunaybased tetrahedralization algorithms. Second, our algorithm is guaranteed to produce a valid tetrahedral mesh with floating-point vertex coordinates, while TetWild produces a valid mesh with rational coordinates which is not guaranteed to be valid after floating-point conversion. As a trade-off, our algorithm no longer guarantees that all input triangles are present in the output mesh, but in practice, as confirmed by our tests on the Thingi10k dataset, the algorithm always succeeds in inserting all input triangles.
[
Paper]
[
Code]
[
Figures]
[
Data]
[
Talk]
 Incremental Potential Contact: Intersection- and Inversion-free, Large-Deformation Dynamics
Incremental Potential Contact: Intersection- and Inversion-free, Large-Deformation Dynamics
Minchen Li,
Zachary Ferguson,
Teseo Schneider,
Timothy Langlois,
Denis Zorin,
Daniele Panozzo,
Chenfanfu Jiang,
Danny M. Kaufman,
ACM Transaction on Graphics (SIGGRAPH) , 2020
Contacts weave through every aspect of our physical world, from daily household chores to acts of nature. Modeling and predictive computation of these phenomena for solid mechanics is important to every discipline concerned with the motion of mechanical systems, including engineering and animation. Nevertheless, efficiently time-stepping accurate and consistent simulations of real-world contacting elastica remains an outstanding computational challenge. To model the complex interaction of deforming solids in contact we propose Incremental Potential Contact (IPC) -- a new model and algorithm for variationally solving implicitly time-stepped nonlinear elastodynamics. IPC maintains an intersection- and inversion-free trajectory regardless of material parameters, time step sizes, impact velocities, severity of deformation, or boundary conditions enforced. Constructed with a custom nonlinear solver, \IPC enables efficient resolution of time-stepping problems with separate, user-exposed accuracy tolerances that allow independent specification of the physical accuracy of the dynamics and the geometric accuracy of surface-to-surface conformation. This enables users to decouple, as needed per application, desired accuracies for a simulation's dynamics and geometry. The resulting time stepper solves contact problems that are intersection-free (and thus robust), inversion-free, efficient (at speeds comparable to or faster than available methods that lack both convergence and feasibility), and accurate (solved to user-specified accuracies). To our knowledge this is the first implicit time-stepping method, across both the engineering and graphics literature that can consistently enforce these guarantees as we vary simulation parameters. In an extensive comparison of available simulation methods, research libraries and commercial codes we confirm that available engineering and computer graphics methods, while each succeeding admirably in custom-tuned regimes, often fail with instabilities, egregious constraint violations and/or inaccurate and implausible solutions, as we vary input materials, contact numbers and time step. We also exercise IPC across a wide range of existing and new benchmark tests and demonstrate its accurate solution over a broad sweep of reasonable time-step sizes and beyond (up to $h=2$s) across challenging large-deformation, large-contact stress-test scenarios with meshes composed of up to 2.3M tetrahedra and processing up to 498K contacts per time step. For applications requiring high-accuracy we demonstrate tight convergence on all measures. While, for applications requiring lower accuracies, e.g. animation, we confirm IPC can ensure feasibility and plausibility even when specified tolerances are lowered for efficiency.
[
Paper]
[
Video]
[
Supplemental Video]
[
Code]
[
S1: Technical]
[
S2: Comparisons]
[
S3: Statistics]
[
Website]
 Reinforcement of General Shell Structures
Reinforcement of General Shell Structures
Francisca Gil Ureta,
Nico Pietroni,
Denis Zorin,
ACM Transaction on Graphics (SIGGRAPH) , 2020
We introduce an efficient method for designing shell reinforcements of min- imal weight. Inspired by classical Michell trusses, we create a reinforcement layout whose members are aligned with optimal stress directions, then opti- mize their shape minimizing the volume while keeping stresses bounded. We exploit two predominant techniques for reinforcing shells: adding ribs aligned with stress directions and using thicker walls on regions of high stress. Most previous work can generate either only ribs or only variable- thickness walls. However, in the general case, neither approach by itself will provide optimal solutions. By using a more precise volume model, our method is capable of producing optimized structures with the full range of qualitative behaviors: from ribs to walls, and smoothly transitioning in between. Our method includes new algorithms for determining the layout of reinforcement structure elements, and an efficient algorithm to optimize their shape, minimizing a non-linear non-convex functional at a fraction of the cost and with better optimality compared to standard solvers. We demonstrate the optimization results for a variety of shapes, and the improvements it yields in the strength of 3D-printed objects.
[
Paper]
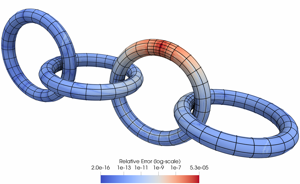 A robust solver for elliptic PDEs in 3D complex geometries
A robust solver for elliptic PDEs in 3D complex geometries
Matthew J. Morse,
Abtin Rahimian,
Denis Zorin,
Arxiv , 2020
We develop a boundary integral equation solver for elliptic partial differential equations on complex 3D geometries. Our method is high-order accurate with optimal O(N) complexity and robustly handles complex geometries. A key component is our singular and near-singular layer potential evaluation scheme, hedgehog : a simple extrapolation of the solution along a line to the boundary. We present a series of geometry-processing algorithms required for hedgehog to run efficiently with accuracy guarantees on arbitrary geometries and an adaptive upsampling scheme based on a iteration-free heuristic for quadrature error that incorporates surface curvature. We validate the accuracy and performance with a series of numerical tests and compare our approach to a competing local evaluation method.
[
Arxiv]
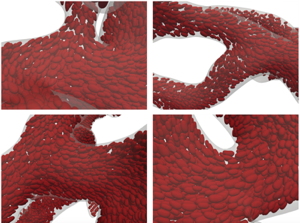 Scalable Simulation of Realistic Volume Fraction Red Blood Cell Flows through Vascular Networks
Scalable Simulation of Realistic Volume Fraction Red Blood Cell Flows through Vascular Networks
Libin Lu,
Matthew J. Morse,
Abtin Rahimian,
Georg Stadler,
Denis Zorin,
SC , 2019
High-resolution blood flow simulations have potential for developing better understanding biophysical phenomena at the microscale, such as vasodilation, vasoconstriction and overall vascular resistance. To this end, we present a scalable platform for the simulation of red blood cell (RBC) flows through complex capillaries by modeling the physical system as a viscous fluid with immersed deformable particles. We describe a parallel boundary integral equation solver for general elliptic partial differential equations, which we apply to Stokes flow through blood vessels. We also detail a parallel collision avoiding algorithm to ensure RBCs and the blood vessel remain contact-free. We have scaled our code on Stampede2 at the Texas Advanced Computing Center up to 34,816 cores. Our largest simulation enforces a contact-free state between four billion surface elements and solves for three billion degrees of freedom on one million RBCs and a blood vessel composed from two million patches.
[
Paper]
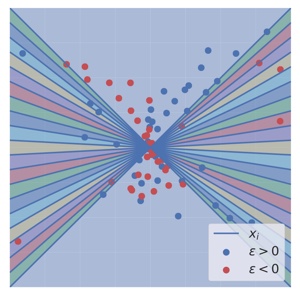 Gradient Dynamics of Shallow Univariate ReLU Networks
Gradient Dynamics of Shallow Univariate ReLU Networks
Francis Williams,
Matthew Trager,
Claudio T. Silva,
Daniele Panozzo,
Denis Zorin,
Joan Bruna,
NeurIPS , 2019
We present a theoretical and empirical study of the gradient dynamics of overparameterized shallow ReLU networks with one-dimensional input, solving least-squares interpolation. We show that the gradient dynamics of such networks are determined by the gradient flow in a non-redundant parameterization of the network function. We examine the principal qualitative features of this gradient flow. In particular, we determine conditions for two learning regimes:kernel and adaptive, which depend both on the relative magnitude of initialization of weights in different layers and the asymptotic behavior of initialization coefficients in the limit of large network widths. We show that learning in the kernel regime yields smooth interpolants, minimizing curvature, and reduces to cubic splines for uniform initializations. Learning in the adaptive regime favors instead linear splines, where knots cluster adaptively at the sample points.
[
Paper]
 TriWild: Robust Triangulation with Curve Constraints
TriWild: Robust Triangulation with Curve Constraints
Yixin Hu,
Teseo Schneider,
Xifeng Gao,
Qingnan Zhou,
Alec Jacobson,
Denis Zorin,
Daniele Panozzo,
ACM Transaction on Graphics (SIGGRAPH) , 2019
We propose a robust 2D meshing algorithm, TriWild, to generate curved triangles reproducing smooth feature curves, leading to coarse meshes designed to match the simulation requirements necessary by applications and avoiding the geometrical errors introduced by linear meshes. The robustness and effectiveness of our technique are demonstrated by batch processing an SVG collection of 20k images, and by comparing our results against state of the art linear and curvilinear meshing algorithms. We demonstrate for our algorithm the practical utility of computing diffusion curves, fluid simulations, elastic deformations, and shape inflation on complex 2D geometries.
[
Paper]
[
Code]
[
Data]
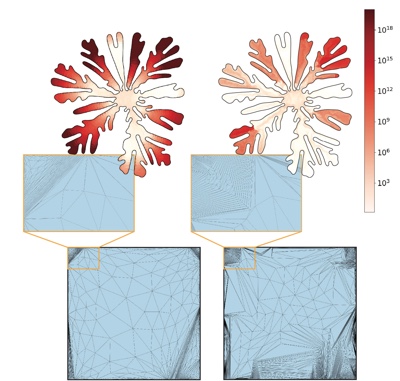 Progressive Embedding
Progressive Embedding
Hanxiao Shen,
Zhongshi Jiang,
Denis Zorin,
Daniele Panozzo,
ACM Transaction on Graphics (SIGGRAPH) , 2019
Tutte embedding is one of the most common building blocks in geometry processing algorithms due to its simplicity and provable guarantees. Although provably correct in infinite precision arithmetic, it fails in challenging cases when implemented using floating point arithmetic, largely due to the induced exponential area changes. We propose Progressive Embedding, with similar theoretical guarantees to Tutte embedding, but more resilient to the rounding error of floating point arithmetic. Inspired by progressive meshes, we collapse edges on an invalid embedding to a valid, simplified mesh, then insert points back while maintaining validity. We demonstrate the robustness of our method by computing embeddings for a large collection of disk topology meshes. By combining our robust embedding with a variant of the matchmaker algorithm, we propose a general algorithm for the problem of mapping multiply connected domains with arbitrary hard constraints to the plane, with applications in texture mapping and remeshing.
[
Paper]
[
Code]
[
Data]
 ABC: A Big CAD Model Dataset For Geometric Deep Learning
ABC: A Big CAD Model Dataset For Geometric Deep Learning
Sebastian Koch,
Albert Matveev,
Zhongshi Jiang,
Francis Williams,
Alexey Artemov,
Evgeny Burnaev,
Marc Alexa,
Denis Zorin,
Daniele Panozzo,
CVPR , 2019
We introduce ABC-Dataset, a collection of one million Computer-Aided Design (CAD) models for research of geometric deep learning methods and applications. Each model is a collection of explicitly parametrized curves and surfaces, providing ground truth for differential quantities, patch segmentation, geometric feature detection, and shape reconstruction. Sampling the parametric descriptions of surfaces and curves allows generating data in different formats and resolutions, enabling fair comparisons for a wide range of geometric learning algorithms. As a use case for our dataset, we perform a large-scale benchmark for estimation of surface normals, comparing existing data driven methods and evaluating their performance against both the ground truth and traditional normal estimation methods.
[
Paper]
[
Supplemental]
[
Website]
[
Data]
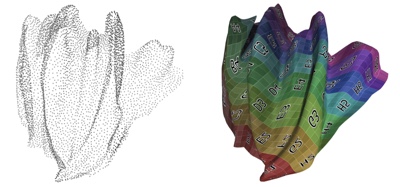 Deep Geometric Prior for Surface Reconstruction
Deep Geometric Prior for Surface Reconstruction
Francis Williams,
Teseo Schneider,
Claudio T. Silva,
Denis Zorin,
Joan Bruna,
Daniele Panozzo,
CVPR , 2019
The reconstruction of a discrete surface from a point cloud is a fundamental geometry processing problem that has been studied for decades, with many methods developed. We propose the use of a deep neural network as a geometric prior for surface reconstruction. Specifically, we overfit a neural network representing a local chart parameterization to part of an input point cloud using the Wasserstein distance as a measure of approximation. By jointly fitting many such networks to overlapping parts of the point cloud, while enforcing a consistency condition, we compute a manifold atlas. By sampling this atlas, we can produce a dense reconstruction of the surface approximating the input cloud. The entire procedure does not require any training data or explicit regularization, yet, we show that it is able to perform remarkably well: not introducing typical overfitting artifacts, and approximating sharp features closely at the same time. We experimentally show that this geometric prior produces good results for both man-made objects containing sharp features and smoother organic objects, as well as noisy inputs. We compare our method with a number of well-known reconstruction methods on a standard surface reconstruction benchmark.
[
Paper]
[
Supplemental]
[
Code]
 Parallel contact-aware simulations of deformable particles in 3D Stokes flow
Parallel contact-aware simulations of deformable particles in 3D Stokes flow
Libin Lu,
Abtin Rahimian,
Denis Zorin,
Arxiv (submitted), 2018
We present a parallel-scalable method for simulating non-dilute suspensions of deformable particles immersed in Stokesian fluid in three dimensions. A critical component in these simulations is robust and accurate collision handling. This work complements our previous work [L. Lu, A. Rahimian, and D. Zorin. Contact-aware simulations of particulate Stokesian suspensions. Journal of Computational Physics 347C: 160-182] by extending it to 3D and by introducing new parallel algorithms for collision detection and handling. We use a well-established boundary integral formulation with spectral Galerkin method to solve the fluid flow. The key idea is to ensure an interference-free particle configuration by introducing explicit contact constraints into the system. While such constraints are typically unnecessary in the formulation they make it possible to eliminate catastrophic loss of accuracy in the discretized problem by preventing contact explicitly. The incorporation of contact constraints results in a significant increase in stable time-step size for locally-implicit time-stepping and a reduction in the necessary number of discretization points for stability. Our method maintains the accuracy of previous methods at a significantly lower cost for dense suspensions and the time step size is independent from the volume fraction. Our method permits simulations with high volume fractions; we report results with up to 60% volume fraction. We demonstrated the parallel scaling of the algorithms on up to 16K CPU cores.
[
Paper]
 Poly-Spline Finite Element Method
Poly-Spline Finite Element Method
Teseo Schneider,
Jeremie Dumas,
Xifeng Gao,
Mario Botsch,
Daniele Panozzo,
Denis Zorin,
ACM Transaction on Graphics , 2019
We introduce an integrated meshing and finite element method pipeline enabling black-box solution of partial differential equations in the volume enclosed by a boundary representation. We construct a hybrid hexahedral-dominant mesh, which contains a small number of star-shaped polyhedra, and build a set of high-order basis on its elements, combining triquadratic B-splines, triquadratic hexahedra (27 degrees of freedom), and harmonic elements. We demonstrate that our approach converges cubically under refinement, while requiring around 50% of the degrees of freedom than a similarly dense hexahedral mesh composed of triquadratic hexahedra. We validate our approach solving Poisson's equation on a large collection of models, which are automatically processed by our algorithm, only requiring the user to provide boundary conditions on their surface.
[
Paper]
[
Code]
[
Data]
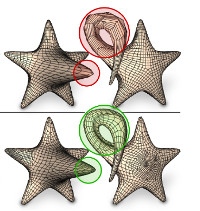 Quadrangulation of non-rigid objects using deformation metrics
Quadrangulation of non-rigid objects using deformation metrics
Jiaran Zhou,
Marcel Campen,
Denis Zorin,
Changhe Tu,
Claudio T. Silva,
Computer Aided Geometric Design , 2018
We present a novel method to generate quad meshes for non-rigid objects. Our method takes into account the geometry of a collection of key poses in one-to-one correspondence or even an entire animation sequence. From this input, on a common computational domain, an extremal metric is computed that captures the local worst case behavior in terms of distortion as the object undergoes deformation. An anisotropic, non-uniformly sized quad mesh is then generated based on this metric. This mesh avoids undersampling when deformed into any of the poses specified in the input and thus reduces artifacts. Hence, in contrast to previous approaches which target static geometry, our method aims to optimize the mesh's adaptation to the shape for every pose expected during animation or deformation rather than for one specific reference state.
[
Paper]
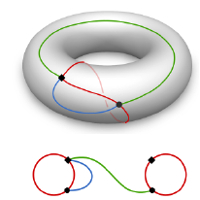 Seamless Parametrization with Arbitrarily Prescribed Cones
Seamless Parametrization with Arbitrarily Prescribed Cones
Marcel Campen,
Hanxiao Shen,
Jiaran Zhou,
Denis Zorin,
Arxiv (submitted), 2018
Seamless global parametrization of surfaces is a key operation in geometry processing, e.g. for high-quality quad mesh generation. A common approach is to prescribe the parametric domain structure, in particular the locations of parametrization singularities (cones), and solve a non-convex optimization problem minimizing a distortion measure, with local injectivity imposed through either constraints or barrier terms. In both cases, an initial valid parametrization is essential to serve as feasible starting point for obtaining an optimized solution. While convexified versions of the constraints eliminate this initialization requirement, they narrow the range of solutions, causing some problem instances that actually do have a solution to become infeasible. We demonstrate that for arbitrary given sets of topologically admissible parametric cones with prescribed curvature, a global seamless parametrization always exists (with the exception of one well-known case). Importantly, our proof is constructive and directly leads to a general algorithm for computing such parametrizations. Most distinctively, this algorithm is bootstrapped with a convex optimization problem (solving for a conformal map), in tandem with a simple linear equation system (determining a seamless modification of this map). This initial map can then serve as valid starting point and be optimized with respect to application specific distortion measures using existing injectivity preserving methods.
[
Paper]
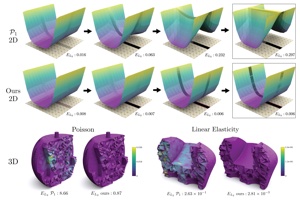 Decoupling Simulation Accuracy from Mesh Quality
Decoupling Simulation Accuracy from Mesh Quality
Teseo Schneider,
Yixin Hu,
Jeremie Dumas,
Xifeng Gao,
Daniele Panozzo,
Denis Zorin,
ACM Transaction on Graphics (SIGGRAPH Asia) , 2018
For a given PDE problem, three main factors affect the accuracy of FEM solutions: basis order, mesh resolution, and mesh element quality. The first two factors are easy to control, while controlling element shape quality is a challenge, with fundamental limitations on what can be achieved. We propose to use p-refinement (increasing element degree) to decouple the approximation error of the finite element method from the domain mesh quality for elliptic PDEs. Our technique produces an accurate solution even on meshes with badly shaped elements, with a slightly higher running time due to the higher cost of high-order elements. We demonstrate that it is able to automatically adapt the basis to badly shaped elements, ensuring an error consistent with high-quality meshing, without any per-mesh parameter tuning. Our construction reduces to traditional fixed-degree FEM methods on high-quality meshes with identical performance. Our construction decreases the burden on meshing algorithms, reducing the need for often expensive mesh optimization and automatically compensates for badly shaped elements, which are present due to boundary constraints or limitations of current meshing methods. By tackling mesh generation and finite element simulation jointly, we obtain a pipeline that is both more efficient and more robust than combinations of existing state of the art meshing and FEM algorithms.
[
Paper]
[
Code]
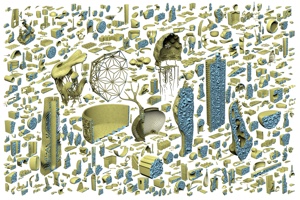 Tetrahedral Meshing in the Wild
Tetrahedral Meshing in the Wild
Yixin Hu,
Qingnan Zhou,
Xifeng Gao,
Alec Jacobson,
Denis Zorin,
Daniele Panozzo,
ACM Transaction on Graphics (SIGGRAPH) , 2018
We propose a novel tetrahedral meshing technique that is unconditionally robust, requires no user interaction, and can directly convert a triangle soup into an analysis-ready volumetric mesh. The approach is based on several core principles: (1) initial mesh construction based on a fully robust, yet efficient, filtered exact computation (2) explicit (automatic or user-defined) tolerancing of the mesh relative to the surface input (3) iterative mesh improvement with guarantees, at every step, of the output validity. The quality of the resulting mesh is a direct function of the target mesh size and allowed tolerance: increasing allowed deviation from the initial mesh and decreasing the target edge length both lead to higher mesh quality. Our approach enables "black-box" analysis, i.e. it allows to automatically solve partial differential equations on geometrical models available in the wild, offering a robustness and reliability comparable to, e.g., image processing algorithms, opening the door to automatic, large scale processing of real-world geometric data.
[
Paper]
[
Code]
[
Figure Data]
[
10k Input]
[
10k Output Surface Meshes]
[
10k Output Tetrahedral Meshes]
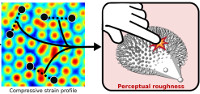 A Quantitative Perceptual Model for Tactile Roughness
A Quantitative Perceptual Model for Tactile Roughness
Chelsea Tymms,
Esther P Gardner,
Denis Zorin,
ACM Transaction on Graphics , 2018
Everyone uses the sense of touch to explore the world, and roughness is one of the most important qualities in tactile perception. Roughness is a major identifier for judgments of material composition, comfort, and friction, and it is tied closely to manual dexterity. The advent of high-resolution 3D printing technology provides the ability to fabricate arbitrary 3D textures with surface geometry that confers haptic properties. In this work, we address the problem of mapping object geometry to tactile roughness. We fabricate a set of carefully designed stimuli and use them in experiments with human subjects to build a perceptual space for roughness. We then match this space to a quantitative model obtained from strain fields derived from elasticity simulations of the human skin contacting the texture geometry, drawing from past research in neuroscience and psychophysics. We demonstrate how this model can be applied to predict and alter surface roughness, and we show several applications in the context of fabrication.
[
Paper]
 A parameteric class of composites with a large achievable range of effective elastic properties
A parameteric class of composites with a large achievable range of effective elastic properties
Igor Ostanin,
George Ovchinnikov,
Davi Colli Tozoni,
Denis Zorin,
Journal of the Mechanics and Physics of Solids , 2018
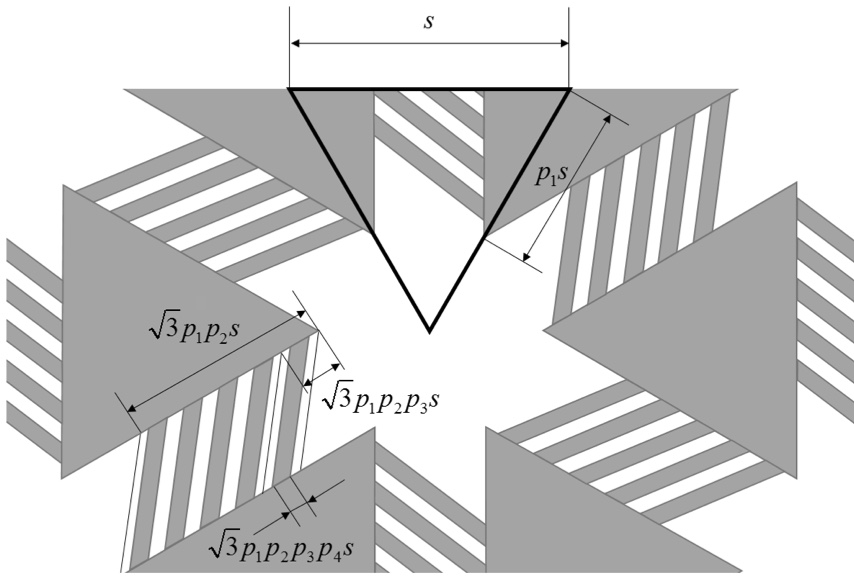
In this paper we investigate numerically an instance of the problem of G-closure for two-dimensional periodic metamaterials. Specifically, we consider composites with isotropic homogenized elasticity tensor, obtained as a mixture of two isotropic materials, focusing on the case of a single material with voids. This problem is important, in particular, in the context of designing small-scale structures for metamaterials in the context of additive fabrication, as this type of metamaterials makes it possible to obtain a range of material properties using a single base material. We demonstrate that two closely related simple parametric families based on the structure proposed by O. Sigmund attain good coverage of the space of isotropic properties satisfying Hashin-Shtrikman bounds. In particular, for positive Poisson ratio, we demonstrate that Hashin-Shtrikman bound can be approximated arbitrarily well, within limits imposed by numerical approximation: a strong evidence that these bounds are achievable in this case. For negative Poisson ratios, we numerically obtain a bound which we hypothesize to be close to optimal, at least for metamaterials with rotational symmetries of a regular triangle tiling.
[
Paper]
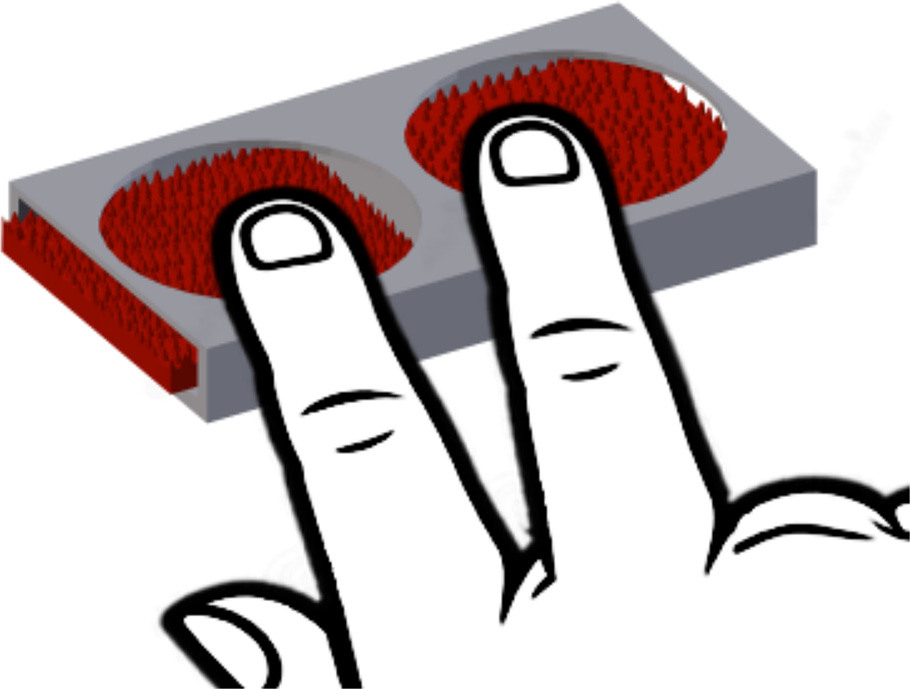 Tactile perception of the roughness of 3D-printed textures
Tactile perception of the roughness of 3D-printed textures
Chelsea Tymms,
Denis Zorin,
Esther P Gardner,
Journal of Neurophysiology , 2017
Surface roughness is one of the most important qualities in haptic perception. Roughness is a major identifier for judgments of material composition, comfort, and friction and is tied closely to manual dexterity. Some attention has been given to the study of roughness perception in the past, but it has typically focused on noncontrollable natural materials or on a narrow range of artificial materials. The advent of high-resolution three-dimensional (3D) printing technology provides the ability to fabricate arbitrary 3D textures with precise surface geometry to be used in tactile studies. We used parametric modeling and 3D printing to manufacture a set of textured plates with defined element spacing, shape, and arrangement. Using active touch and two-alternative forced-choice protocols, we investigated the contributions of these surface parameters to roughness perception in human subjects. Results indicate that large spatial periods produce higher estimations of roughness (with Weber fraction_=_0.19), small texture elements are perceived as rougher than large texture elements of the same wavelength, perceptual differences exist between textures with the same spacing but different arrangements, and roughness equivalencies exist between textures differing along different parameters. We posit that papillary ridges serve as tactile processing units, and neural ensembles encode the spatial profiles of the texture contact area to produce roughness estimates. The stimuli and the manufacturing process may be used in further studies of tactile roughness perception and in related neurophysiological applications.
[
Paper]
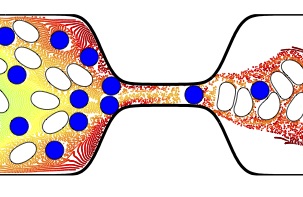 Contact-aware simulations of particulate Stokesian suspensions
Contact-aware simulations of particulate Stokesian suspensions
Libin Lu,
Abtin Rahimian,
Denis Zorin,
Journal of Computational Physics , 2017
We present an efficient, accurate, and robust method for simulation of dense suspensions of deformable and rigid particles immersed in Stokesian fluid in two dimensions. We use a well-established boundary integral formulation for the problem as the foundation of our approach. This type of formulation, with a high-order spatial discretization and an implicit and adaptive time discretization, have been shown to be able to handle complex interactions between particles with high accuracy. Yet, for dense suspensions, very small time-steps or expensive implicit solves as well as a large number of discretization points are required to avoid non-physical contact and intersections between particles, leading to infinite forces and numerical instability. Our method maintains the accuracy of previous methods at a significantly lower cost for dense suspensions. The key idea is to ensure interference-free configuration by introducing explicit contact constraints into the system. While such constraints are unnecessary in the formulation, in the discrete form of the problem, they make it possible to eliminate catastrophic loss of accuracy by preventing contact explicitly. Introducing contact constraints results in a significant increase in stable time-step size for explicit time-stepping, and a reduction in the number of points adequate for stability.
[
Paper]
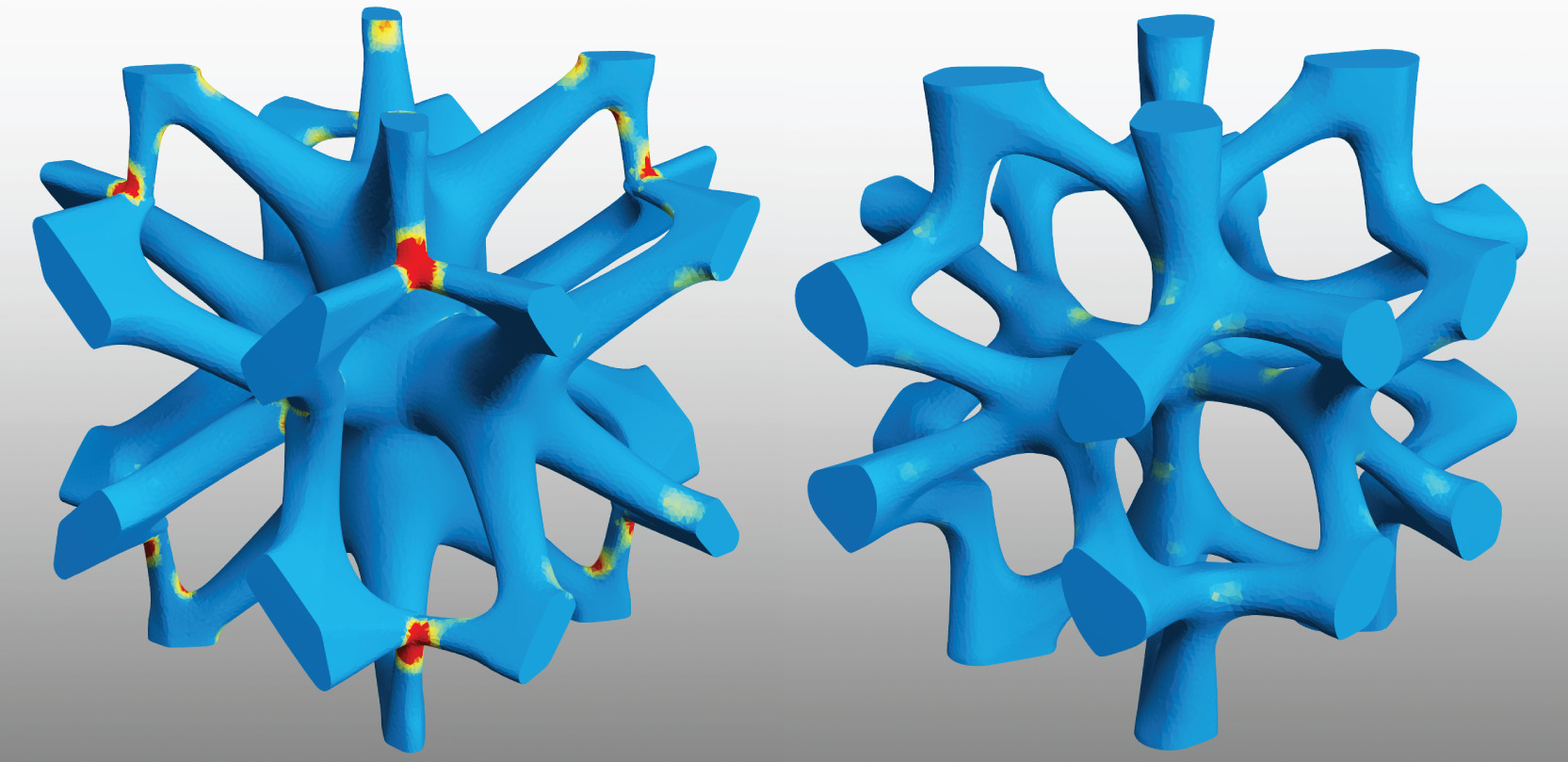 Worst-case stress relief for microstructures
Worst-case stress relief for microstructures
Julian Panetta,
Abtin Rahimian,
Denis Zorin,
ACM Transactions on Graphics (TOG) , 2017
Additive fabrication technologies are limited by the types of material they can print: while the technologies are continuously improving, still only a relatively small discrete set of materials can be used in each printed object. At the same time, the low cost of introducing geometric complexity suggests the alternative of controlling the elastic material properties by producing microstructures, which can achieve behaviors significantly differing from the solid printing material. While promising results have been obtained in this direction, fragility is a significant problem blocking practical applications, especially for achieving soft material properties: due to stress concentrations at thin joints, deformations and repeated loadings are likely to cause fracture. We present a set of methods to minimize stress concentrations in microstructures by evolving their shapes. First, we demonstrate that the worst-case stress analysis problem (maximizing a stress measure over all possible unit loads) has an exact solution for periodic microstructures. We develop a new, accurate discretization of the shape derivative for stress objectives and introduce a low-dimensional parametric shape model for microstructures. This model supports robust minimization of maximal stress (approximated by an Lp norm with high p) and an efficient implementation of printability constraints. In addition to significantly reducing stresses (by a typical factor of 5X), the new method substantially expands the range of effective material properties covered by the collection of structures.
[
Paper]
 Similarity maps and field-guided T-splines: a perfect couple
Similarity maps and field-guided T-splines: a perfect couple
Marcel Campen,
Denis Zorin,
ACM Transactions on Graphics (SIGGRAPH) , 2017
A variety of techniques were proposed to model smooth surfaces based on tensor product splines (e.g. subdivision surfaces, free-form splines, T-splines). Conversion of an input surface into such a representation is commonly achieved by constructing a global seamless parametrization, possibly aligned to a guiding cross-field (e.g. of principal curvature directions), and using this parametrization as domain to construct the spline-based surface. One major fundamental difficulty in designing robust algorithms for this task is the fact that for common types, e.g. subdivision surfaces (requiring a conforming domain mesh) or T-spline surfaces (requiring a globally consistent knot interval assignment) reliably obtaining a suitable parametrization that has the same topological structure as the guiding field poses a major challenge. Even worse, not all fields do admit suitable parametrizations, and no concise conditions are known as to which fields do. We present a class of surface constructions (T-splines with halfedge knots) and a class of parametrizations (seamless similarity maps) that are, in a sense, a perfect match for the task: for any given guiding field structure, a compatible parametrization of this kind exists and a smooth piecewise rational surface with exactly the same structure as the input field can be constructed from it. As a byproduct, this enables full control over extraordinary points. The construction is backward compatible with classical NURBS. We present efficient algorithms for building discrete conformal similarity maps and associated T-meshes and T-spline surfaces.
[
Paper]
[
Code]
 Surface Networks
Surface Networks
Ilya Kostrikov,
Zhongshi Jiang,
Daniele Panozzo,
Denis Zorin,
Joan Bruna,
CVPR (Oral Presentation) , 2018
We study data-driven representations for three-dimensional triangle meshes, which are one of the prevalent objects used to represent 3D geometry. Recent works have developed models that exploit the intrinsic geometry of manifolds and graphs, namely the Graph Neural Networks (GNNs) and its spectral variants, which learn from the local metric tensor via the Laplacian operator. Despite offering excellent sample complexity and built-in invariances, intrinsic geometry alone is invariant to isometric deformations, making it unsuitable for many applications. To overcome this limitation, we propose several upgrades to GNNs to leverage extrinsic differential geometry properties of three-dimensional surfaces, increasing its modeling power. In particular, we propose to exploit the Dirac operator, whose spectrum detects principal curvature directions --- this is in stark contrast with the classical Laplace operator, which directly measures mean curvature. We coin the resulting model the \emph{Surface Network (SN)}. We demonstrate the efficiency and versatility of SNs on two challenging tasks: temporal prediction of mesh deformations under non-linear dynamics and generative models using a variational autoencoder framework with encoders/decoders given by SNs.
[
Paper]
[
Supplemental]
[
Code]
 On Discrete Conformal Seamless Similarity Maps
On Discrete Conformal Seamless Similarity Maps
Marcel Campen,
Denis Zorin,
Arxiv , 2017
An algorithm for the computation of global discrete conformal parametrizations with prescribed global holonomy signatures for triangle meshes was recently described in [Campen and Zorin 2017]. In this paper we provide a detailed analysis of convergence and correctness of this algorithm. We generalize and extend ideas of [Springborn et al. 2008] to show a connection of the algorithm to Newton's algorithm applied to solving the system of constraints on angles in the parametric domain, and demonstrate that this system can be obtained as a gradient of a convex energy
[
Paper]
 Ubiquitous evaluation of layer potentials using Quadrature by Kernel-Independent Expansion
Ubiquitous evaluation of layer potentials using Quadrature by Kernel-Independent Expansion
Abtin Rahimian,
Alex Barnett,
Denis Zorin,
BIT Numerical Mathematics , 2016
We introduce a quadrature scheme QBKIX for the ubiquitous high-order accurate evaluation of singular layer potentials associated with general elliptic PDEs, i.e., a scheme that yields high accuracy at all distances to the domain boundary as well as on the boundary itself. Relying solely on point evaluations of the underlying kernel, our scheme is essentially PDE-independent; in particular, no analytic expansion nor addition theorem is required. Moreover, it applies to boundary integrals with singular, weakly singular, and hypersingular kernels. Our work builds upon quadrature by expansion, which approximates the potential by an analytic expansion in the neighborhood of each expansion center. In contrast, we use a sum of fundamental solutions lying on a ring enclosing the neighborhood, and solve a small dense linear system for their coefficients to match the potential on a smaller concentric ring. We test the new method with Laplace, Helmholtz, Yukawa, Stokes, and Navier (elastostatic) kernels in two dimensions (2D) using adaptive, panel-based boundary quadratures on smooth and corner domains. Advantages of the algorithm include its relative simplicity of implementation, immediate extension to new kernels, dimension-independence (allowing simple generalization to 3D), and compatibility with fast algorithms such as the kernel-independent FMM.
[
Paper]
 Scale-Invariant Directional Alignment of Surface Parametrizations
Scale-Invariant Directional Alignment of Surface Parametrizations
Marcel Campen,
Moritz Ibing,
Hans-Christian Ebke,
Denis Zorin,
Leif Kobbelt,
Computer Graphics Forum (SGP) , 2016
Various applications of global surface parametrization benefit from the alignment of parametrization isolines with principal curvature directions. This is particularly true for recent parametrization-based meshing approaches, where this directly translates into a shape-aware edge flow, better approximation quality, and reduced meshing artifacts. Existing methods to influence a parametrization based on principal curvature directions suffer from scale-dependence, which implies the necessity of parameter variation, or try to capture complex directional shape features using simple 1D curves. Especially for non-sharp features, such as chamfers, fillets, blends, and even more for organic variants thereof, these abstractions can be unfit. We present a novel approach which respects and exploits the 2D nature of such directional features, detects them based on coherence and homogeneity properties, and controls the parametrization process accordingly. This approach enables us to provide an intuitive, scale-invariant control parameter to the user. It also allows us to consider non-local aspects like the topology of a feature, enabling further improvements. We demonstrate that, compared to previous approaches, global parametrizations of higher quality can be generated without user intervention.
[
Paper]
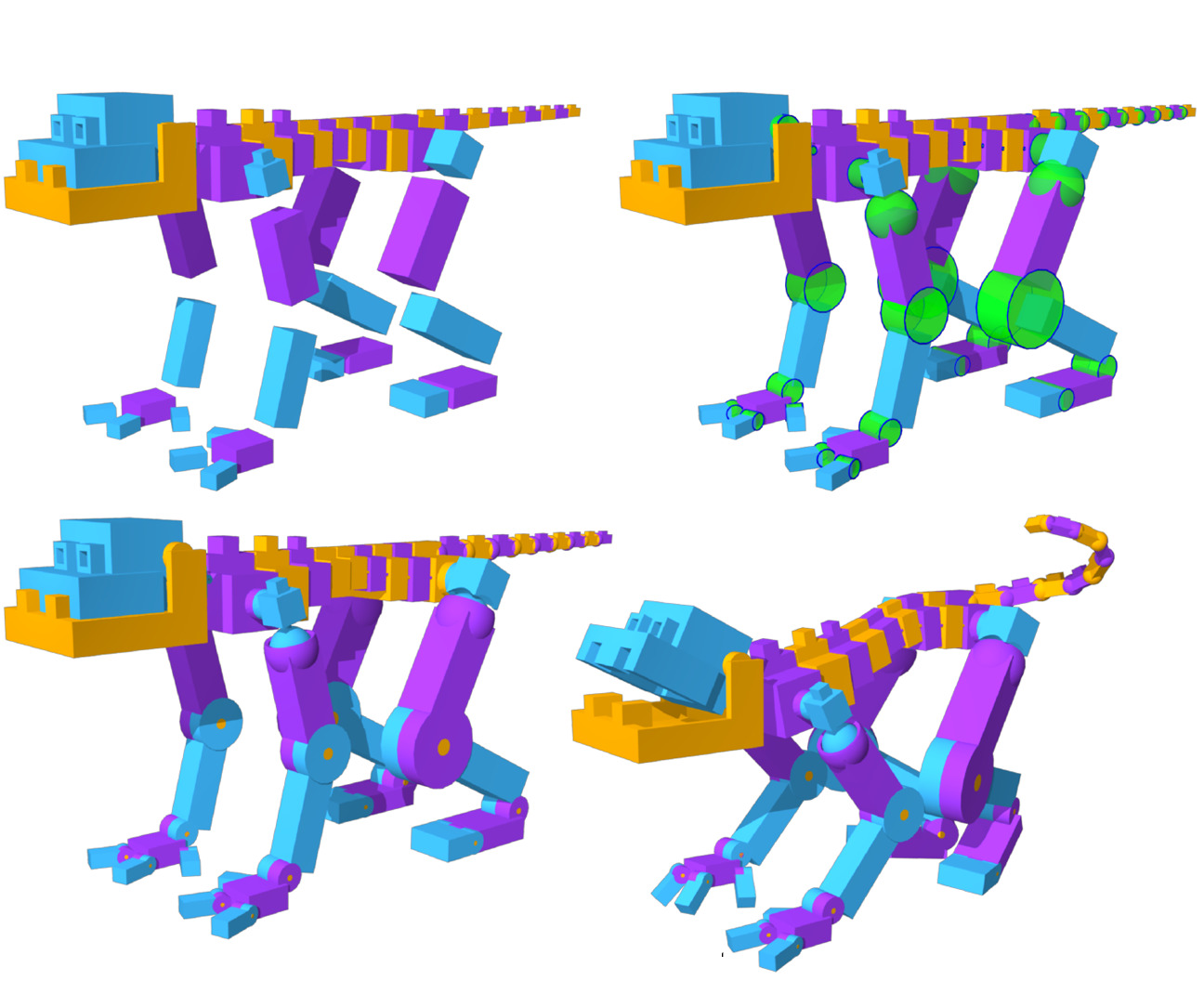 Interactive Modeling of Mechanical Objects
Interactive Modeling of Mechanical Objects
Francisca Gil Ureta,
Chelsea Tymms,
Denis Zorin,
Computer Graphics Forum (SGP) , 2016
Objects with various types of mechanical joints are among the most commonly built. Joints implement a vocabulary of simple constrained motions (kinematic pairs) that can be used to build more complex behaviors. Defining physically correct joint geometry is crucial both for realistic appearance of models during motion, as these are typically the only parts of geometry that stay in contact, and for fabrication. Direct design of joint geometry often requires more effort than the design of the rest of the object geometry, as it requires design of components that stay in precise contact, are aligned with other parts, and allow the desired range of motion. We present an interactive system for creating physically realizable joints with user-controlled appearance. Our system minimizes or, in most cases, completely eliminates the need for the user to manipulate low-level geometry of joints. This is achieved by automatically inferring a small number of plausible combinations of joint dimensions, placement and orientation from part geometry, with the user making the final high-level selection based on object semantic. Through user studies, we demonstrate that functional results with a satisfying appearance can be obtained quickly by users with minimal modeling experience, offering a significant improvement in the time required for joint construction, compared to standard modeling approaches.
[
Paper]
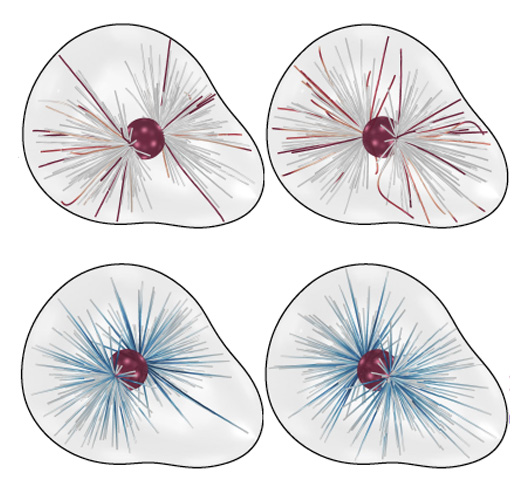 A fast platform for simulating flexible fiber suspensions applied to cell mechanics
A fast platform for simulating flexible fiber suspensions applied to cell mechanics
Ehssan Nazockdast,
Abtin Rahimian,
Denis Zorin,
Michael Shelley,
Journal of Computational Physics , 2017
We present a novel platform for the large-scale simulation of fibrous structures immersed in a Stokesian fluid and evolving under confinement or in free-space. One of the main motivations for this work is to study the dynamics of fiber assemblies within biological cells. For this, we also incorporate the key biophysical elements that determine the dynamics of these assemblies, which include the polymerization and depolymerization kinetics of fibers, their interactions with molecular motors and other objects, their flexibility, and hydrodynamic coupling. This work, to our knowledge, is the first technique to include many-body hydrodynamic interactions (HIs), and the resulting fluid flows, in cellular fiber assemblies. We use the non-local slender body theory to compute the fluid-structure interactions of the fibers and a second-kind boundary integral formulation for other rigid bodies and the confining boundary. A kernel-independent implementation of the fast multiple method is utilized for efficient evaluation of HIs. The deformation of the fibers is described by the nonlinear Euler-Bernoulli beam theory and their polymerization is modeled by the reparametrization of the dynamic equations in the appropriate non-Lagrangian frame. We use a pseudo-spectral representation of fiber positions and implicit HIs in the time-stepping to resolve large fiber deformations, and to allow time-steps not constrained by temporal stiffness or fiber-fiber interactions. The entire computational scheme is parallelized, which enables simulating assemblies of thousands of fibers. We use our method to investigate two important questions in the mechanics of cell division: (i) the effect of confinement on the hydrodynamic mobility of microtubule asters; and (ii) the dynamics of the positioning of mitotic spindle in complex cell geometries. Finally to demonstrate the general applicability of the method, we simulate the sedimentation of a cloud of fibers.
[
Paper]
 Bijective maps from simplicial foliations
Bijective maps from simplicial foliations
Marcel Campen,
Claudio T. Silva,
Denis Zorin,
ACM Transactions on Graphics (TOG) , 2016
This paper presents a method for bijective parametrization of 2D and 3D objects over canonical domains. While a range of solutions for the two-dimensional case are well-known, our method guarantees bijectivity of mappings also for a large, combinatorially-defined class of tetrahedral meshes (shellable meshes). The key concept in our method is the piecewise-linear (PL) foliation, decomposing the mesh into one-dimensional submanifolds and reducing the mapping problem to parametrization of a lower-dimensional manifold (a foliation section). The maps resulting from these foliations are proved to be bijective and continuous, and shown to have provably bijective PL approximations. We describe exact, numerically robust evaluation methods and demonstrate our implementation's capabilities on a large variety of meshes.
[
Paper]
 Mesh Arrangements for Solid Geometry
Mesh Arrangements for Solid Geometry
Qingnan Zhou,
Eitan Grinspun,
Denis Zorin,
Alec Jacobson,
ACM Transactions on Graphics (TOG) , 2016
Many high-level geometry processing tasks rely on low-level constructive solid geometry operations. Though trivial for implicit representations, boolean operations are notoriously difficult to execute robustly for explicit boundary representations. Existing methods for 3D triangle meshes fall short in one way or another. Some methods are fast but fail to produce closed, self-intersection free output. Other methods are robust but place prohibitively strict assumptions on the input, e.g., no hollow cavities, non-manifold edges or selfintersections. We propose a systematic recipe for conducting a family of exact constructive solid geometry operations. The two-stage method makes no general position assumptions and does not resort to numerical perturbation. The method is variadic, operating on any number of input meshes. This generalizes unary mesh-repair operations, classic binary boolean differencing, and n-ary operations such as finding all regions inside at least k out of n inputs. We demonstrate the superior effectiveness and robustness of our method on a dataset of 10,000 "real-world" meshes from a popular online repository. To encourage development, validation, and comparison, we release both our code and dataset to the public.
[
Paper]
[
Code]
 A Tensor-Train accelerated solver for integral equations in complex geometries
A Tensor-Train accelerated solver for integral equations in complex geometries
Eduardo Corona,
Abtin Rahimian,
Denis Zorin,
Journal of Computational Physics , 2017
We present a framework using the Tensor Train decomposition (TT) to accurately and efficiently solve volume and boundary integral equations in three dimensions. We describe how the TT decomposition can be used as a hierarchical compression and inversion scheme for matrices arising from the discretization of integral equations. For a broad range of problems, computational and storage costs of the inversion scheme are extremely modest O(logN) and once the inverse is computed, it can be applied in O(N logN). We analyze the TT ranks for hierarchically low rank matrices and discuss its relationship to commonly used hierarchical compression techniques such as FMM, HSS, and wavelets. We prove that the TT ranks are bounded for translation-invariant systems and argue that this behavior extends to non-translation invariant volume and boundary integrals. For volume integrals, the TT decomposition provides an efficient direct solver requiring significantly less memory compared to other fast direct solvers. We present results demonstrating the remarkable performance of the TT-based solver when applied to both translation and non-translation invariant volume integrals in 3D. For boundary integral equations, we demonstrate that using a TT decomposition to construct preconditioners for a Krylov subspace method leads to an efficient and robust solver with a small memory footprint. We test the TT preconditioners in the iterative solution of an exterior elliptic boundary value problem (Laplace) formulated as a boundary integral equation in complex, multiply connected geometries.
[
Paper]
 Boundary Integral Method for the Flow of Vesicles with Viscosity Contrast in Three Dimensions
Boundary Integral Method for the Flow of Vesicles with Viscosity Contrast in Three Dimensions
Abtin Rahimian,
Shravan Veerapaneni,
Denis Zorin,
George Biros,
Journal of Computational Physics , 2015
We propose numerical algorithms for the simulation of the dynamics of three- dimensional vesicles suspended in viscous Stokesian fluid. Our method is an extension of our previous work to flows with viscosity contrast.This generalization requires a change in the boundary integral formulation of the solution, in which a double-layer Stokes integral is introduced, and leads to changes in the fluid dynamics due to the viscosity contrast of the vesicles, which can no longer be efficiently resolved with existing algorithms. In this paper we describe the algorithms needed to handle flows with viscosity contrast accurately and efficiently. We show that a globally semi-implicit method does not have any time-step stability constraint for flows with single and multiple vesicles with moderate viscosity contrast and the computational cost per simulation unit time is comparable to or less than that of an explicit scheme. Automatic oversampling adaptation enables us to achieve high accuracy with very low spectral resolution. We conduct numerical experiments to investigate the stability, accuracy, and the computational cost of the algorithms. Overall, our method achieves several orders of magnitude speed-up compared to the standard explicit schemes.
[
Paper]
 Elastic Textures
Elastic Textures
Julian Panetta,
Qingnan Zhou,
Luigi Malmo,
Nico Pietroni,
Paolo Cignoni,
Denis Zorin,
ACM Transactions on Graphics (TOG) , 2015
We introduce elastic textures: a set of parametric, tileable, printable, cubic patterns achieving a broad range of isotropic elastic material properties: the softest pattern is over a thousand times softer than the stiffest, and the Poisson's ratios range from below zero to nearly 0.5. Using a combinatorial search over topologies followed by shape optimization, we explore a wide space of truss-like, symmetric 3D patterns to obtain a small family. This pattern family can be printed without internal support structure on a single-material 3D printer and can be used to fabricate objects with prescribed mechanical behavior. The family can be extended easily to create anisotropic patterns with target orthotropic properties. We demonstrate that our elastic textures are able to achieve a user-supplied varying material property distribution. We also present a material optimization algorithm to choose material properties at each point within an object to best fit a target deformation under a prescribed scenario. We show that, by fabricating these spatially varying materials with elastic textures, the desired behavior is achieved.
[
Paper]
[
Video]
 Dyadic T-mesh subdivision
Dyadic T-mesh subdivision
Denis Kovacs,
Denis Zorin,
ACM Transactions on Graphics (TOG) , 2015
Meshes with T-joints (T-meshes) and related high-order surfaces have many advantages in situations where flexible local refinement is needed. At the same time, designing subdivision rules and bases for T-meshes is much more difficult, and fewer options are available. For common geometric modeling tasks it is desirable to retain the simplicity and flexibility of commonly used subdivision surfaces, and extend them to handle T-meshes. We propose a subdivision scheme extending Catmull-Clark and NURSS to a special class of quad T-meshes, dyadic T-meshes, which have no more than one T-joint per edge. Our scheme is based on a factorization with the same structure as Catmull-Clark subdivision. On regular T-meshes it is a refinement scheme for a subset of standard T-splines. While we use more variations of subdivision masks compared to Catmull-Clark and NURSS, the minimal size of the stencil is maintained, and all variations in formulas are due to simple changes in coefficients.
[
Paper]
 An O (N) direct solver for integral equations on the plane
An O (N) direct solver for integral equations on the plane
Eduardo Corona,
Per-Gunnar Martinsson,
Denis Zorin,
Applied and Computational Harmonic Analysis , 2015
An efficient direct solver for volume integral equations with O(N) complexity for a broad range of problems is presented. The solver relies on hierarchical compression of the discretized integral operator, and exploits that off-diagonal blocks of certain dense matrices have numerically low rank. Technically, the solver is inspired by previously developed direct solvers for integral equations based on "recursive skeletonization" and "Hierarchically Semi-Separable" (HSS) matrices, but it improves on the asymptotic complexity of existing solvers by incorporating an additional level of compression. The resulting solver has optimal O(N) complexity for all stages of the computation, as demonstrated by both theoretical analysis and numerical examples. The computational examples further display good practical performance in terms of both speed and memory usage. In particular, it is demonstrated that even problems involving 10^{7} unknowns can be solved to precision 10^{-10} using a simple Matlab implementation of the algorithm executed on a single core.
[
Paper]
 Strict minimizers for geometric optimization
Strict minimizers for geometric optimization
Zohar Levi,
Denis Zorin,
ACM Transactions on Graphics (TOG) , 2014
We introduce the idea of {strict minimizers for geometric distortion measures used in shape interpolation, deformation, parametrization, and other applications involving geometric mappings. The L-infinity norm ensures the tightest possible control on the worst-case distortion. Unfortunately, it does not yield a unique solution and does not distinguish between solutions with high or low distortion below the maximum. The strict minimizer is a minimal L-infinity norm solution, which always prioritizes higher distortion reduction. We propose practical algorithms for computing strict minimizers. We also offer an efficient algorithm for L-infinity optimization based on the ARAP energy. This algorithm can be used on its own or as a building block for an ARAP strict minimizer. We demonstrate that these algorithms lead to significant improvements in quality.
[
Paper]
 Smoothness of Subdivision Surfaces with Boundary
Smoothness of Subdivision Surfaces with Boundary
Henning Biermann,
Sara Grundel,
Denis Zorin,
Constructive Approximation , 2014
Subdivision rules for meshes with boundary are essential for practical applications of subdivision surfaces. These rules have to result in piecewise C^k-continuous boundary limit curves, and ensure C^k-continuity of the surface itself. We present in this paper general necessary and sufficient conditions for C^k-continuity of subdivision schemes for surfaces with boundary, and specialize these to practially applicable sufficient conditions for C^1-continuity. We use these conditions to show that certain boundary rules for Loop and Catmull-Clark are in fact C^1 continuous.
[
Paper]
 Locally Injective Parametrization with Arbitrary Fixed Boundaries
Locally Injective Parametrization with Arbitrary Fixed Boundaries
Ofir Weber,
Denis Zorin,
ACM Transactions on Graphics (TOG) , 2014
We present an algorithm for mapping a triangle mesh, which is homeomorphic to a disk, to a planar domain with arbitrary fixed boundaries. The algorithm is guaranteed to produce a globally bijective map when the boundary is fixed to a shape that does not self-intersect. Obtaining a one-to-one map is of paramount importance for many graphics applications such as texture mapping. However, for other applications, such as quadrangulation, remeshing, and planar deformations, global bijectively may be unnecessarily constraining and requires significant increase on map distortion. For that reason, our algorithm allows the fixed boundary to intersect itself, an d is guaranteed to produce a map that is injective locally (if such a map exists
[
Paper]
 Robust Field-aligned Global Parametrization
Robust Field-aligned Global Parametrization
Ashish Myles,
Nico Pietroni,
Denis Zorin,
ACM Transactions on Graphics (TOG) , 2014
We present a robust method for computing locally bijective global parametrizations aligned with a given cross-field. The singularities of the parametrization in general agree with singularities of the field, except in a small number of cases when several additional cones need to be added in a controlled way. Parametric lines can be constrained to follow an arbitrary set of feature lines on the surface. Our method is based on constructing an initial quad patch partition using robust cross-field integral line tracing. This process is followed by an algorithm modifying the quad layout structure to ensure that consistent parametric lengths can be assigned to the edges. For most meshes, the layout modification algorithm does not add new singularities; a small number of singularities may be added to resolve an explicitly described set of layouts. We demonstrate that our algorithm succeeds on a test data set of over a hundred meshes.
[
Paper]
[
Additional]
[
Data]
 Quad-Mesh Generation and Processing: A Survey
Quad-Mesh Generation and Processing: A Survey
David Bommes,
Bruno Levy,
Nico Pietroni,
Enrico Puppo,
Claudio T. Silva,
Marco Tarini,
Denis Zorin,
Computer Graphics Forum , 2013
Triangle meshes have been nearly ubiquitous in computer graphics, and a large body of data structures and geometry processing algorithms based on them has been developed in the literature. At the same time, quadrilateral meshes, especially semi-regular ones, have advantages for many applications, and significant progress was made in quadrilateral mesh generation and processing during the last several years. In this survey we discuss the advantages and problems of techniques operating on quadrilateral meshes, including surface analysis and mesh quality, simplification, adaptive refinement, alignment with features, parametrisation and remeshing
[
Paper]
 Subspace integration with local deformations
Subspace integration with local deformations
David Harmon,
Denis Zorin,
ACM Transactions on Graphics (TOG) , 2013
Subspace techniques greatly reduce the cost of nonlinear simulation by approximating deformations with a small custom basis. In order to represent the deformations well (in terms of a global metric), the basis functions usually have global support, and cannot capture localized deformations. While reduced-space basis functions can be localized to some extent, capturing truly local deformations would still require a very large number of precomputed basis functions, significantly degrading both precomputation and online performance. We present an efficient approach to handling local deformations that cannot be predicted, most commonly arising from contact and collisions, by augmenting the subspace basis with custom functions derived from analytic solutions to static loading problems. We also present a new cubature scheme designed to facilitate fast computation of the necessary runtime quantities while undergoing a changing basis. Our examples yield a two order of magnitude speedup over full-coordinate simulations, striking a desirable balance between runtime speeds and expressive ability.
[
Paper]
[
Video]
 Controlled-distortion constrained global parametrization
Controlled-distortion constrained global parametrization
Ashish Myles,
Denis Zorin,
ACM Transactions on Graphics (TOG) , 2013
The quality of a global parametrization is determined by a number of factors, including amount of distortion, number of singularities (cones), and alignment with features and boundaries. Placement of cones plays a decisive role in determining the overall distortion of the parametrization; at the same time, feature and boundary alignment also affect the cone placement. A number of methods were proposed for automatic choice of cone positions, either based on singularities of cross-fields and emphasizing alignment, or based on distortion optimization. In this paper we describe a method for placing cones for seamless global parametrizations with alignment constraints. We use a close relation between variation-minimizing cross-fields and related 1-forms and conformal maps, and demonstrate how it leads to a constrained optimization problem formulation. We show for boundary-aligned parametrizations metric distortion may be reduced by cone chains, sometimes to an arbitrarily small value, and the trade-off between the distortion and the number of cones can be controlled by a regularization term. Constrained parametrizations computed using our method have significantly lower distortion compared to the state-of-the art field-based method, yet maintain feature and boundary alignment. In the most extreme cases, parametrization collapse due to alignment constraints is eliminated.
[
Paper]
 Worst-case structural analysis
Worst-case structural analysis
Qingnan Zhou,
Julian Panetta,
Denis Zorin,
ACM Transactions on Graphics (TOG) , 2013
Direct digital manufacturing is a set of rapidly evolving technologies that provide easy ways to manufacture highly customized and unique products. The development pipeline for such products is radically different from the conventional manufacturing pipeline: 3D geometric models are designed by users often with little or no manufacturing experience, and sent directly to the printer. Structural analysis on the user side with conventional tools is often unfeasible as it requires specialized training and software. Trial-and-error, the most common approach, is time-consuming and expensive. We present a method that would identify structural problems in objects designed for 3D printing based on geometry and material properties only, without specific assumptions on loads and manual load setup. We solve a constrained optimization problem to determine the "worst" load distribution for a shape that will cause high local stress or large deformations. While in its general form this optimization has a prohibitively high computational cost, we demonstrate that an approximate method makes it possible to solve the problem rapidly for a broad range of printed models. We validate our method both computationally and experimentally and demonstrate that it has good predictive power for a number of diverse 3D printed shapes.
[
Paper]
 A massively parallel adaptive fast multipole method on heterogeneous architectures
A massively parallel adaptive fast multipole method on heterogeneous architectures
Ilya Lashuk,
Aparna Chandramowlishwaran,
Harper Langston,
Tuan-Anh Nguyen,
Rahul Sampath,
Aashay Shringarpure,
Richard Vuduc,
Lexing Ying,
Denis Zorin,
George Biros,
Communications of the ACM , 2012
We describe a parallel fast multipole method (FMM) for highly nonuniform distributions of particles. We employ both distributed memory parallelism (via MPI) and shared memory parallelism (via OpenMP and GPU acceleration) to rapidly evaluate two-body nonoscillatory potentials in three dimensions on heterogeneous high performance computing architectures. We have performed scalability tests with up to 30 billion particles on 196,608 cores on the AMD/CRAY-based Jaguar system at ORNL. On a GPU-enabled system (NSF's Keeneland at Georgia Tech/ORNL), we observed 30x speedup over a single core CPU and 7x speedup over a multicore CPU implementation. By combining GPUs with MPI, we achieve less than 10 ns/particle and six digits of accuracy for a run with 48 million nonuniformly distributed particles on 192 GPUs.
[
Paper]
 Fields on symmetric surfaces
Fields on symmetric surfaces
Daniele Panozzo,
Yaron Lipman,
Enrico Puppo,
Denis Zorin,
ACM Transactions on Graphics (TOG) , 2012
Direction fields, line fields and cross fields are used in a variety of computer graphics applications ranging from non-photorealistic rendering to remeshing. In many cases, it is desirable that fields adhere to symmetry, which is predominant in natural as well as man-made shapes. We present an algorithm for designing smooth N-symmetry fields on surfaces respecting generalized symmetries of the shape, while maintaining alignment with local features. Our formulation for constructing symmetry fields is based on global symmetries, which are given as input to the algorithm, with no isometry assumptions. We explore in detail the properties of generalized symmetries (reflections in particular), and we also develop an algorithm for the robust computation of such symmetry maps, based on a small number of correspondences, for surfaces of genus zero.
[
Paper]
[
Addendum]
 Global parametrization by incremental flattening
Global parametrization by incremental flattening
Ashish Myles,
Denis Zorin,
ACM Transactions on Graphics (TOG) , 2012
Global parametrization of surfaces requires singularities (cones) to keep distortion minimal. We describe a method for finding cone locations and angles and an algorithm for global parametrization which aim to produce seamless parametrizations with low metric distortion. The idea of the method is to evolve the metric of the surface, starting with the original metric so that a growing fraction of the area of the surface is constrained to have zero Gaussian curvature; the curvature becomes gradually concentrated at a small set of vertices which become cones. We demonstrate that the resulting parametrizations have significantly lower metric distortion compared to previously proposed methods.
[
Paper]
 Computing extremal quasiconformal maps
Computing extremal quasiconformal maps
Ofir Weber,
Ashish Myles,
Denis Zorin,
Computer Graphics Forum (Best Paper Award), 2012
Conformal maps are widely used in geometry processing applications. They are smooth, preserve angles, and are locally injective by construction. However, conformal maps do not allow for boundary positions to be prescribed. A natural extension to the space of conformal maps is the richer space of quasiconformal maps of bounded conformal distortion. Extremal quasiconformal maps, that is, maps minimizing the maximal conformal distortion, have a number of appealing properties making them a suitable candidate for geometry processing tasks. Similarly to conformal maps, they are guaranteed to be locally bijective; unlike conformal maps however, extremal quasiconformal maps have sufficient flexibility to allow for solution of boundary value problems. Moreover, in practically relevant cases, these solutions are guaranteed to exist, are unique and have an explicit characterization. We present an algorithm for computing piecewise linear approximations of extremal quasiconformal maps for genus-zero surfaces with boundaries, based on Teichm��_��__��_��___��_��__��_��____��_��__��_��___��_��__��_��_____ller's characterization of the dilatation of extremal maps using holomorphic quadratic differentials. We demonstrate that the algorithm closely approximates the maps when an explicit solution is available and exhibits good convergence properties for a variety of boundary conditions.
[
Paper]
 Global parametrization of range image sets
Global parametrization of range image sets
Nico Pietroni,
Marco Tarini,
Olga Sorkine-Hornung,
Denis Zorin,
ACM Transactions on Graphics , 2011
We present a method to globally parameterize a surface represented by height maps over a set of planes (range images). In contrast to other parametrization techniques, we do not start with a manifold mesh. The parametrization we compute defines a manifold structure, it is seamless and globally smooth, can be aligned to geometric features and shows good quality in terms of angle and area preservation, comparable to current parametrization techniques for meshes. Computing such global seamless parametrization makes it possible to perform quad remeshing, texture mapping and texture synthesis and many other types of geometry processing operations. Our approach is based on a formulation of the Poisson equation on a manifold structure defined for the surface by the range images. Construction of such global parametrization requires only a way to project surface data onto a set of planes, and can be applied directly to implicit surfaces, nonmanifold surfaces, very large meshes, and collections of range scans. We demonstrate application of our technique to all these geometry types.
[
Paper]
 Asynchronous integration with phantom meshes
Asynchronous integration with phantom meshes
David Harmon,
Qingnan Zhou,
Denis Zorin,
ACM SIGGRAPH/Eurographics Symposium on Computer Animation , 2011
Asynchronous variational integration of layered contact models provides a framework for robust collision handling, correct physical behavior, and guaranteed eventual resolution of even the most dif?cult contact problems. Yet, even for low-contact scenarios, this approach is signi?cantly slower compared to its less robust alternatives ��_��__��_��___��_��__��_��____��_��__��_��___��_��__��_��_____ often due to handling of stiff elastic forces in an explicit framework. We propose a method that retains the guarantees, but allows for variational implicit integration of some of the forces, while maintaining asynchronous integration needed for contact handling. Our method uses phantom meshes for calculations with stiff forces, which are then coupled to the original mesh through constraints. We use the augmented discrete Lagrangian of the constrained system to derive a variational integrator with the desired conservation properties.
[
Paper]
 Manifold-based surfaces with boundary
Manifold-based surfaces with boundary
Elif Tosun,
Denis Zorin,
Computer-Aided Geometric Design , 2011
We present a manifold-based surface construction extending the C1 construction of Ying and Zorin (2004a). Our surfaces allow for pircewise-smooth boundaries, have user-controlled arbitrary degree of smoothness and improved derivative and visual behavior. 2-flexibility of our surface construction is confirmed numerically for a range of local mesh configurations.
[
Paper]
 A fast algorithm for simulating vesicle flows in three dimensions
A fast algorithm for simulating vesicle flows in three dimensions
Shravan Veerapaneni,
Abtin Rahimian,
George Biros,
Denis Zorin,
Journal of Computational Physics , 2011
Vesicles are locally-inextensible fluid membranes that can sustain bending. In this paper, we present a fast algorithm for simulating the dynamics of vesicles suspended in viscous fluids. Spatial quantities are discretized using spherical harmonics, and quadrature rules for singular surface integrals need to be adapted to this case; an algorithm for surface reparameterization is neeed to ensure suffcient of the time- stepping scheme, and spectral filtering is introduced to maintain reasonable accuracy while minimizing computational costs. We obtain a time-stepping scheme that, in our numerical experiments, is unconditionally stable. We present results to analyze the cost and convergence rates of the overall scheme. To illustrate the applicability of the new method, we consider a few vesicle-flow interaction problems: a single vesicle in relaxation, sedimentation, shear flows, and many-vesicle flows.
[
Paper]
[
Video 1]
[
Video 2]
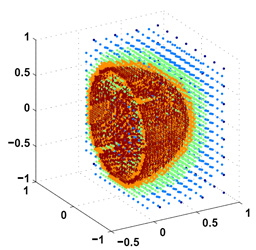 A Free-space adaptive FMM-Based PDE solver in three dimensions
A Free-space adaptive FMM-Based PDE solver in three dimensions
M. Harper Langston,
Leslie Greengard,
Denis Zorin,
Communications in Applied Mathematics and Computational Science , 2011
We present a kernel-independent, adaptive fast multipole method (FMM) of arbitrary order accuracy for solving elliptic PDEs in three dimensions with radiation boundary conditions. The algorithm requires only a Green's function evaluation routine for the governing equation and a representation of the source distribution (the right-hand side) that can be evaluated at arbitrary points. The performance of the FMM is accelerated in two ways. First, we construct a piecewise polynomial approximation of the right-hand side and compute far-field expansions in the FMM from the coefficients of this approximation. Second, we precompute tables of quadratures to handle the near-field interactions on adaptive octree data structures, keeping the total storage requirements in check through the exploitation of symmetries. We present numerical examples for the Laplace, modified Helmholtz and Stokes equations.
[
Paper]
 Interference Aware Geometric Modeling
Interference Aware Geometric Modeling
David Harmon,
Daniele Panozzo,
Olga Sorkine-Hornung,
Denis Zorin,
ACM Transactions on Graphics (SIGGRAPH Asia) , 2011
While often a requirement for geometric models, there has been little research in resolving the interaction of deforming surfaces during real-time modeling sessions. To address this important topic, we introduce an interference algorithm specifically designed for the domain of geometric modeling. This algorithm is general, easily working within existing modeling paradigms to maintain their important properties. Our algorithm is fast, and is able to maintain interactive rates on complex deforming meshes of over 75K faces, while robustly removing intersections. Lastly, our method is controllable, allowing fine-tuning to meet the specific needs of the user. This includes support for minimum separation between surfaces and control over the relative rigidity of interacting objects.
[
Paper]
[
Video]
[
Code]
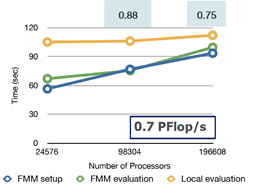 Petascale Direct Numerical Simulation of Blood Flow on 200K Cores and Heterogeneous Architectures.
Petascale Direct Numerical Simulation of Blood Flow on 200K Cores and Heterogeneous Architectures.
Abtin Rahimian,
Ilya Lashuk,
Shravan Veerapaneni,
Aparna Chandramowlishwaran,
Dhairya Malhotra,
Logan Moon,
Rahul Sampath,
Aashay Shringarpure,
Jeffrey Vetter,
Richard Vuduc,
Denis Zorin,
George Biros,
ACM/IEEE conference on Supercomputing (Gordon Bell Prize), 2010
We present a fast, petaflop-scalable algorithm for Stokesian particulate flows. Our goal is the direct simulation of blood, which we model as a mixture of a Stokesian fluid (plasma) and red blood cells (RBCs). Directly simulating blood is a challenging multiscale, multiphysics problem. We report simulations with up to 200 million deformable RBCs. The largest simulation amounts to 90 billion unknowns in space. In terms of the number of cells, we improve the state-of-the art by several orders of magnitude: the previous largest simulation, at the same physical fidelity as ours, resolved the flow of O(1,000-10,000) RBCs. Our approach has three distinct characteristics: (1) we faithfully represent the physics of RBCs by using nonlinear solid mechanics to capture the deformations of each cell; (2) we accurately resolve the long-range, N-body, hydrodynamic interactions between RBCs (which are caused by the surrounding plasma); and (3) we allow for the highly non-uniform distribution of RBCs in space. The new method has been implemented in the software library MOBO (for "Moving Boundaries"). We designed MOBO to support parallelism at all levels, including inter-node distributed memory parallelism, intra-node shared memory parallelism, data parallelism (vectorization), and fine-grained multithreading for GPUs. We have implemented and optimized the majority of the computation kernels on both Intel/AMD x86 and NVidia's Tesla/Fermi platforms for single and double floating point precision. Overall, the code has scaled on 256 CPU-GPUs on the Teragrid's Lincoln cluster and on 200,000 AMD cores of the Oak Ridge national Laboratory's Jaguar PF system. In our largest simulation, we have achieved 0.7 Petaflops/s of sustained performance on Jaguar.
[
Paper]
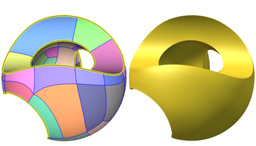 Feature-aligned T-meshes
Feature-aligned T-meshes
Ashish Myles,
Nico Pietroni,
Denis Kovacs,
Denis Zorin,
ACM Transactions on Graphics , 2010
High-order and regularly sampled surface representations are more efficient and compact than general meshes and considerably simplify many geometric modeling and processing algorithms. A number of recent algorithms for conversion of arbitrary meshes to regularly sampled form (typically quadrangulation) aim to align the resulting mesh with feature lines of the geometry. While resulting in a substantial improvement in mesh quality, feature alignment makes it difficult to obtain coarse regular patch partitions of the mesh. In this paper, we propose an approach to constructing patch layouts consisting of small numbers of quadrilateral patches while maintaining good feature alignment. To achieve this, we use quadrilateral T-meshes, for which the intersection of two faces may not be the whole edge or vertex, but a part of an edge. T-meshes offer more flexibility for reduction of the number of patches and vertices in a base domain while maintaining alignment with geometric features. At the same time, T-meshes retain many desirable features of quadrangulations, allowing construction of high-order representations, easy packing of regularly sampled geometric data into textures, as well as supporting different types of discretizations for physical simulation.
[
Paper]
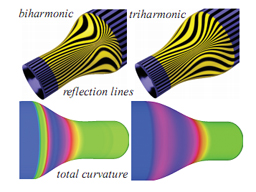 Mixed Finite Elements for Variational Surface Modeling
Mixed Finite Elements for Variational Surface Modeling
Alec Jacobson,
Elif Tosun,
Olga Sorkine-Hornung,
Denis Zorin,
Computer Graphics Forum , 2010
Many problems in geometric modeling can be described using variational formulations that define the smoothness of the shape and its behavior w.r.t. the posed modeling constraints. For example, high-quality C2 surfaces that obey boundary conditions on positions, tangents and curvatures can be conveniently defined as solutions of high-order geometric PDEs; the advantage of such a formulation is its conceptual representation-independence. In practice, solving high-order problems efficiently and accurately for surfaces approximated by meshes is notoriously difficult. For modeling applications, the preferred approach is to use discrete geometric schemes which are efficient and robust, but their convergence properties are less well understood compared to higher-order FEM. In this paper, we explore discretizations of common geometric PDEs on meshes using mixed finite elements, where additional variables for the derivatives in the problem are introduced. Such formulations use first-order derivatives only, allowing a discretization with simple linear elements. Various boundary conditions can be naturally discretized in this setting. We formalize continuous region constraints commonly used in modeling applications, and show that these seamlessly fit into the mixed framework. We demonstrate that some of the commonly used discrete geometric discretizations can be regarded as a particular case of mixed finite elements. We study the convergence behavior of our discretizations, and how they can be applied to implement common modeling tasks.
[
Paper]
 Anisotropic quadrangulation
Anisotropic quadrangulation
Denis Kovacs,
Ashish Myles,
Denis Zorin,
Symposium on Solid and Physical Modeling , 2010
Quadrangulation algorithms approximate arbitrary meshes with meshes consisting of quads or mostly quads, and with only a small number of extraordinary vertices. To minimize the number of quads needed while maintaing a good approximation of shapes, one wants to use anisotropically scaled quads in areas with a high ratio of principal curvatures. Most existing techniques rely on global parametrization methods either producing uniform aspect-ratio quads, or anisotropic quads with sizes unrelated to the curvature magnitudes. We propose a simple technique that can be combined with a variety of parametrization and quadrangulation methods to produce anisotropic semiregular remeshing. Our approach is based on using a metric derived from the shape operator to adjust lengths and angles in surface parametrization equations in a way that equalizes normal error distribution over the surface.
[
Paper]
 Real-time creased subdivision surfaces
Real-time creased subdivision surfaces
Denis Kovacs,
Jason Mitchell,
Denis Zorin,
IEEE Transactions on Visualization and Computer Graphics ((also in Proceedings of I3D, 2009)), 2010
We present an extension of recently developed Loop and Schaefer's approximation of Catmull-Clark surfaces (ACC) for surfaces with creases and corners which are essential for most applications. We discuss the integration of ACC into Valve's Source game engine and analyze performance of our implementation
[
Paper]
 A massively parallel adaptive fast-multipole method on heterogeneous architectures
A massively parallel adaptive fast-multipole method on heterogeneous architectures
Ilya Lashuk,
Aparna Chandramowlishwaran,
Harper Langston,
Tuan-Anh Nguyen,
Rahul Sampath,
Aashay Shringarpure,
Richard Vuduc,
Lexing Ying,
Denis Zorin,
George Biros,
ACM/IEEE conference on Supercomputing (Best Paper Award Nomination), 2009
We present new scalable algorithms and a new implementation of our kernel-independent fast multipole method (Ying et al. ACM/IEEE SC '03), in which we employ both distributed memory parallelism (via MPI) and shared memory/streaming parallelism (via GPU acceleration) to rapidly evaluate two-body non-oscillatory potentials. On traditional CPU-only systems, our implementation scales well up to 30 billion unknowns on 65K cores (AMD/CRAY-based Kraken system at NSF/NICS) for highly non-uniform point distributions. On GPU-enabled systems, we achieve 30x speedup for problems of up to 256 million points on 256 GPUs (Lincoln at NSF/NCSA) over a comparable CPU-only based implementations. We achieve scalability to such extreme core counts by adopting a new approach to scalable MPI-based tree construction and partitioning, and a new reduction algorithm for the evaluation phase. For the sub-components of the evaluation phase (the direct- and approximate-interactions, the target evaluation, and the source-to-multipole translations), we use NVIDIA's CUDA framework for GPU acceleration to achieve excellent performance. To do so requires carefully constructed data structure transformations, which we describe in the paper and whose cost we show is minor. Taken together, these components show promise for ultrascalable FMM in the petascale era and beyond.
[
Paper]
 High-order methods for simulating the dynamics of axis-symmetric inextensible vesicles in viscous flow
High-order methods for simulating the dynamics of axis-symmetric inextensible vesicles in viscous flow
Shravan Veerapaneni,
Denis Gueyffier,
George Biros,
Denis Zorin,
Journal of Computational Physics , 2009
We extend the efficient high-order method of [Veerapaneni et al., 2008] to the axisymmetric flows with immersed vesicles of spherical or toroidal topology. In this case, the bending and fluid forces require a siginficantly different (for bending forces, nonlinear, vs. linear in 2D) case computation. The qualitative numerical behavior of the problem is also different: with a nonlinear semi-implicit scheme needed to eliminate the CFL-type restriction in the toroidal case. We present an unconditionally stable scheme with low cost per time step, and spectrally accurate in space and third-order accurate in time. An important part of the algorithm is a novel numerical scheme for evaluation of the 3D Stokes single-layer potential on an axisymmetric surface, needed to achieve optimal complexity. As an application, we explore the motion of axisymmetric vesicles under gravity
[
Paper]
 Application-aware management of parallel simulation
Application-aware management of parallel simulation
Siu-Man Yau,
Vijay Karamcheti,
Denis Zorin,
Kostadin Damevski,
Steven G. Parker,
SIGPLAN Symposium on Principles and Practice of Parallel Programming , 2009
This paper presents a system deployed on parallel clusters to manage a collection of parallel simulations that make up a computational study. It explores how such a system can extend traditional parallel job scheduling and resource allocation techniques to incorporate knowledge specific to the study. Using a UINTAH-based helium gas simulation code (ARCHES) and the SimX system for multi-experiment computational studies, this paper demonstrates that, by using application-specific knowledge in resource allocation and scheduling decisions, one can reduce the run time of a computational study from over 20 hours to under 4.5 hours on a 32-processor cluster, and from almost 11 hours to just over 3.5 hours on a 64-processor cluster.
[
Paper]
 Structured annotations for 2D-to-3D modeling
Structured annotations for 2D-to-3D modeling
Yotam Gingold,
Takeo Igarashi,
Denis Zorin,
ACM Transactions on Computer Graphics , 2009
We present a single-view 2D interface for 3D modeling based on the idea of placing 2D primitives and annotations on an existing, pre-made sketch or image. Our interface frees users to create 2D sketches from arbitrary angles using their preferred tool -- including pencil and paper -- which they then "describe" using our tool to create a 3D model. Our interface can be used to generate a 3D model from an illustration, such as those found in children's picture books. Our primitives are manipulated with persistent, dynamic handles, and our annotations take the form of markings commonly used in geometry textbooks. Our interface eliminates the constant rotation inherent to previous sketch-based-modeling tools such as [Igarashi et al. 1999]. Our method is significantly different from computer vision approaches because many 2D drawings have no consistent 3D representation. Instead, we view 2D drawings as semantic, qualitative descriptions of 3D geometry, rather than as literal, quantitative descriptions. Our system solves this ill-posed problem with the help of human intervention. Our 3D models are generated entirely from the user's input; our algorithm does not consider the original 2D image. In this work, our focus is on rotund, free-form shapes and not man-made rectilinear/CAD models.
[
Paper]
 A boundary integral method for simulating the dynamics of inextensible vesicles suspended in a viscous fluid in 2D
A boundary integral method for simulating the dynamics of inextensible vesicles suspended in a viscous fluid in 2D
Shravan Veerapaneni,
Denis Gueyffier,
George Biros,
Denis Zorin,
Journal of Computational Physics , 2008
We present a new method for the evolution of inextensible vesicles immersed in a Stokesian fluid. We use a boundary integral formulation for the fluid that results in a set of nonlinear integro-differential equations for the vesicle dynamics. The motion of the vesicles is determined by balancing the nonlocal hydrodynamic forces with the elastic forces due to bending and tension. Numerical simulations of such vesicle motions are quite challenging. On one hand, explicit time-stepping schemes suffer from a severe stability constraint due to the stiffness related to high-order spatial derivatives and a milder constraint due to a transport-like stability condition. On the other hand, an implicit scheme can be expensive because it requires the solution of a set of nonlinear equations at each time step. We present two semi-implicit schemes that circumvent the severe stability constraints on the time step and whose computational cost per time step is comparable to that of an explicit scheme. We discretize the equations by using a spectral method in space, and a multistep third-order accurate scheme in time. We use the fast multipole method (FMM) to efficiently compute vesicle-vesicle interaction forces in a suspension with a large number of vesicles. We report results from numerical experiments that demonstrate the convergence and algorithmic complexity properties of our scheme.
[
Paper]
[
Video 1]
[
Video 2]
[
Video 3]
 Shading-based surface editing
Shading-based surface editing
Yotam Gingold,
Denis Zorin,
ACM Transactions on Computer Graphics , 2008
We present a system for free-form surface modeling that allows a user to modify a shape by changing its rendered, shaded image using stroke-based drawing tools. User input is translated into a set of tangent and positional constraints on the surface. A new shape, whose rendered image closely approximates user input, is computed using an efficient and stable surface optimization procedure. We demonstrate how several types of free-form surface edits which may be difficult to cast in terms of standard deformation approaches can be easily performed using our system.
[
Paper]
[
Video]
 Real-time rendering of textures with feature curves
Real-time rendering of textures with feature curves
Evgueni Parilov,
Denis Zorin,
ACM Transactions on Computer Graphics , 2008
The standard bilinear interpolation on normal maps results in visual artifacts along sharp features, which are common for surfaces with creases, wrinkles, and dents. In many cases, spatially varying features, like the normals near discontinuity curves, are best represented as functions of the distance to the curve and the position along the curve. For high-quality interactive rendering at arbitrary magnifications, one needs to interpolate the distance field preserving discontinuity curves exactly. We present a real-time, GPU-based method for distance function and distance gradient interpolation which preserves discontinuity feature curves. The feature curves are represented by a set of quadratic Bezier curves, with minimal restrictions on their intersections. We demonstrate how this technique can be used for real-time rendering of complex feature patterns and blending normal maps with procedurally defined profiles near normal discontinuities.
[
Paper]
[
Video 1]
[
Video 2]
[
Video 3]
[
Video 4]
[
Video 5]
[
Video 6]
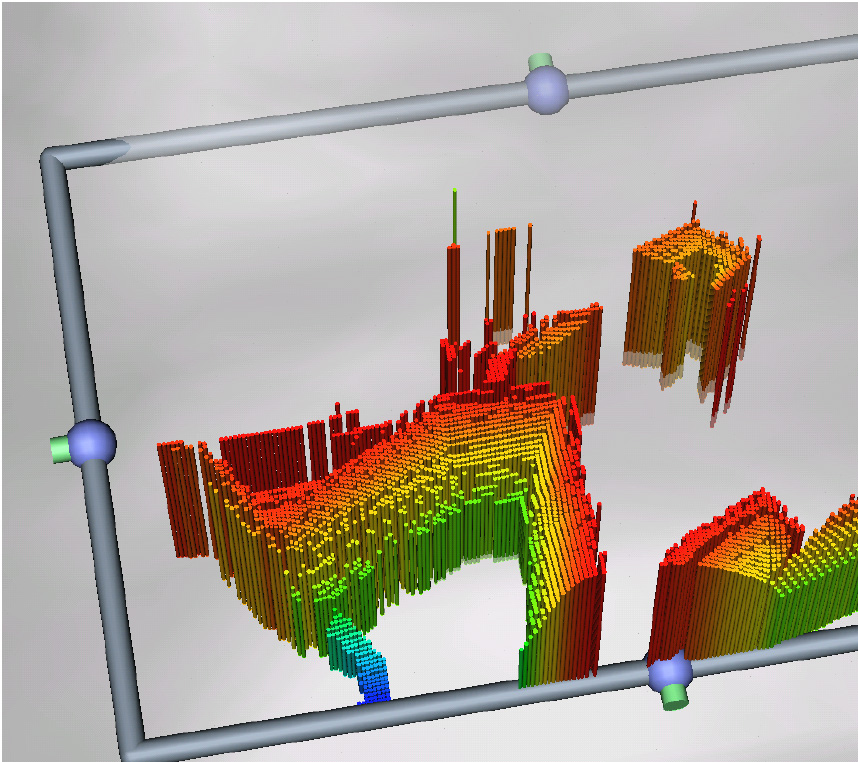 Result reuse in design space exploration: a study in system support for interactive parallel computing
Result reuse in design space exploration: a study in system support for interactive parallel computing
Siu-Man Yau,
Kostadin Damevski,
Vijay Karamcheti,
Steven G. Parker,
Denis Zorin,
IEEE International Parallel and Distributed Processing Symposium , 2008
This paper presents a system supporting reuse of simulation results in multi-experiment computational studies involving independent simulations and explores the benefits of such reuse. Using a SCIRun-based defibrillator device simulation code (DefibSim) and the SimX system for computational studies, this paper demonstrates how aggressive reuse between and within computational studies can enable interactive rates for such studies on a moderate-sized 128-node processor cluster; a brute-force approach to the problem would require two thousand nodes or more on a massively parallel machine for similar performance. Key to realizing these performance improvements is exploiting optimization opportunities that present themselves at the level of the overall workflow of the study as opposed to focusing on individual simulations. Such global optimization approaches are likely to become increasingly important with the shift towards interactive and universal parallel computing.
[
Paper]
 Cubic shells
Cubic shells
Akash Garg,
Eitan Grinspun,
Max Wardetzky,
Denis Zorin,
SIGGRAPH/Eurographics Symposium on Computer Animation , 2007
Hinge-based bending models are widely used in the physically-based animation of cloth, thin plates and shells. We propose a hinge-based model that is simpler to implement, more efficient to compute, and offers a greater number of effective material parameters than existing models. Our formulation builds on two mathematical observations: (a) the bending energy of curved flexible surfaces can be expressed as a cubic polynomial if the surface does not stretch; (b) a general class of anisotropic materials---those that are orthotropic -- is captured by appropriate choice of a single stiffness per hinge. Our contribution impacts a general range of surface animation applications, from isotropic cloth and thin plates to orthotropic fracturing thin shells.
[
Paper]
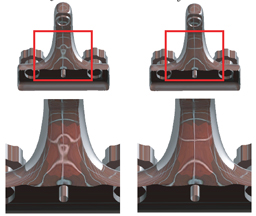 Shape optimization using reflection lines
Shape optimization using reflection lines
Elif Tosun,
Yotam Gingold,
Jason Reisman,
Denis Zorin,
Eurographics/SIGGRAPH Symposium on Geometry Processing , 2007
Many common objects have highly reflective metallic or painted finishes. Their appearance is primarily defined by the distortion the curved shape of the surface introduces in the reflections of surrounding objects. Reflection lines are commonly used for surface interrogation, as they capture many essential aspects of reflection distortion directly, and clearly show surface imperfections that may be hard to see with conventional lighting. In this paper, we propose the use of functionals based on reflection lines for mesh optimization and editing. We describe a simple and efficient discretization of such functionals based on screen-space surface parameterization, and we demonstrate how such discrete functionals can be used for several types of surface editing operations.
[
Paper]
 Controlled-topology filtering
Controlled-topology filtering
Yotam Gingold,
Denis Zorin,
Computer-Aided Design (Previously appeared in Proceedings of SMI 2006), 2007
Many applications require the extraction of isolines and isosurfaces from scalar functions defined on regular grids. These scalar functions may have many different origins: from MRI and CT scan data to terrain data or results of a simulation. As a result of noise and other artifacts, curves and surfaces obtained by standard extraction algorithms often suffer from topological irregularities and geometric noise. While it is possible to remove topological and geometric noise as a post-processing step, in the case when a large number of isolines are of interest there is a considerable advantage in filtering the scalar function directly. While most smoothing filters result in gradual simplification of the topological structure of contours, new topological features typically emerge and disappear during the smoothing process. In this paper, we describe an algorithm for filtering functions defined on regular 2D grids with controlled topology changes, which ensures that the topological structure of the set of contour lines of the function is progressively simplified.
[
Paper]
 Discrete quadratic bending energies
Discrete quadratic bending energies
Max Wardetzky,
Miklos Bergou,
David Harmon,
Denis Zorin,
Eitan Grinspun,
Computer-Aided Geometric Design (Special Issue on Discrete Differential Geometry, extended version of SGP 2006 paper), 2007
We present a family of discrete isometric bending models (IBMs) for triangulated surfaces in 3-space. These models are derived from an axiomatic treatment of discrete Laplace operators, using these operators to obtain linear models for discrete mean curvature from which bending energies are assembled. Under the assumption of isometric surface deformations we show that these energies are quadratic in surface positions. The corresponding linear energy gradients and constant energy Hessians constitute an efficient model for computing bending forces and their derivatives, enabling fast time-integration of cloth dynamics with a two- to three-fold net speedup over existing nonlinear methods, and near-interactive rates for Willmore smoothing of large meshes.
[
Paper]
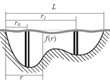 Sim-X: Parallel system software for interactive multi-experiment computational studies
Sim-X: Parallel system software for interactive multi-experiment computational studies
Siu-Man Yau,
Eitan Grinspun,
Vijay Karamcheti,
Denis Zorin,
IEEE International Parallel and Distributed Processing Symposium , 2006
Advances in high-performance computing have led to the broad use of computational studies in everyday engineering and scientific applications. A single study may require thousands of computational experiments, each corresponding to individual runs of simulation software with different parameter settings; in complex studies, the pattern of parameter changes is complex and may have to be adjusted by the user based on partial simulation results. Unfortunately, existing tools have limited high-level support for managing large ensembles of simultaneous computational experiments. In this paper, we present a system architecture for interactive computational studies targeting two goals. The first is to provide a framework for high-level user interaction with computational studies, rather than individual experiments; the second is to maximize the size of the studies that can be performed at close to interactive rates. We describe a prototype implementation of the system and demonstrate performance improvements obtained using our approach for a simple model problem.
[
Paper]
 A High-order 3D boundary integral equation solver for elliptic PDEs in smooth domains
A High-order 3D boundary integral equation solver for elliptic PDEs in smooth domains
Lexing Ying,
George Biros,
Denis Zorin,
Journal of Computational Physics , 2006
We present a high-order boundary integral equation solver for 3D elliptic boundary value problems on domains with smooth boundaries. We use Nystrom's method for discretization, and combine it with special quadrature rules for the singular kernels that appear in the boundary integrals. The overall asymptotic complexity of our method is O(N-3/2), where N is the number of discretization points on the boundary of the domain, and corresponds to linear complexity in the number of uniformly sampled evaluation points. A kernel-independent fast summation algorithm is used to accelerate the evaluation of the discretized integral operators. We describe a high-order accurate method for evaluating the solution at arbitrary points inside the domain, including points close to the domain boundary. We demonstrate how our solver, combined with a regular-grid spectral solver, can be applied to problems with distributed sources. We present numerical results for the Stokes, Navier, and Poisson problems. (c) 2006 Elsevier Inc. All rights reserved.
[
Paper]
 A quadratic bending model for inextensible surfaces
A quadratic bending model for inextensible surfaces
Miklos Bergou,
Max Wardetzky,
David Harmon,
Denis Zorin,
Eitan Grinspun,
Eurographics/SIGGRAPH Symposium on Geometry Processing , 2006
Efficient computation of curvature-based energies is important for practical implementations of geometric modeling and physical simulation applications. Building on a simple geometric observation, we provide a version of a curvature-based energy expressed in terms of the Laplace operator acting on the embedding of the surface. The corresponding energy--being quadratic in positions--gives rise to a constant Hessian in the context of isometric deformations. The resulting isometric bending model is shown to significantly speed up common cloth solvers, and when applied to geometric modeling situations built onWillmore flow to provide runtimes which are close to interactive rates.
[
Paper]
[
Video]
 Constructing curvature-continuous surfaces by blending
Constructing curvature-continuous surfaces by blending
Denis Zorin,
Eurographics/SIGGRAPH Symposium on Geometry Processing , 2006
In this paper we describe an approach to the construction of curvature-continuous surfaces with arbitrary control meshes using subdivision. Using a simple modification of the widely used Loop subdivision algorithm we obtain perturbed surfaces which retain the overall shape and appearance of Loop subdivision surfaces but no longer have flat spots or curvature singularities at extraordinary vertices. Our method is computationally efficient and can be easily added to any existing subdivision code.
[
Paper]
 Computing discrete shape operators on general meshes
Computing discrete shape operators on general meshes
Eitan Grinspun,
Yotam Gingold,
Jason Reisman,
Denis Zorin,
Computer Graphics Forum (Eurographics 2006 Proceedings, 3rd best paper award), 2006
Discrete curvature and shape operators, which capture complete information about directional curvatures at a point, are essential in a variety of applications: simulation of deformable two-dimensional objects, variational modeling and geometric data processing. In many of these applications, objects are represented by meshes. Currently, a spectrum of approaches for formulating curvature operators for meshes exists, ranging from highly accurate but computationally expensive methods used in engineering applications to efficient but less accurate techniques popular in simulation for computer graphics. We propose a simple and efficient formulation for the shape operator for variational problems on general meshes, using degrees of freedom associated with normals. On the one hand, it is similar in its simplicity to some of the discrete curvature operators commonly used in graphics; on the other hand, it passes a number of important convergence tests and produces consistent results for different types of meshes and mesh refinement.
[
Paper]
 A Direct texture placement and editing interface
A Direct texture placement and editing interface
Yotam Gingold,
Philip Davidson,
Jefferson Han,
Denis Zorin,
Proceedings of he 19th ACM Symposium on User Interface Software and Technology (UIST06) , 2006
The creation of most models used in computer animation and computer games requires the assignment of texture coordinates, texture painting, and texture editing. We present a novel approach for texture placement and editing based on direct manipulation of textures on the surface. Compared to conventional tools for surface texturing, our system combines UV-coordinate specification and texture editing into one seamless process, reducing the need for careful initial design of parameterization and providing a natural interface for working with textures directly on 3D surfaces.A combination of efficient techniques for interactive constrained parameterization and advanced input devices makes it possible to realize a set of natural interaction paradigms. The texture is regarded as a piece of stretchable material, which the user can position and deform on the surface, selecting arbitrary sets of constraints and mapping texture points to the surface; in addition, the multi-touch input makes it possible to specify natural handles for texture manipulation using point constraints associated with different fingers. Pressure can be used as a direct interface for texture combination operations. The 3D position of the object and its texture can be manipulated simultaneously using two-hand input.
[
Paper]
[
Video]
 Subdivision on arbitrary meshes: algorithms and theory
Subdivision on arbitrary meshes: algorithms and theory
Denis Zorin,
Institute of Mathematical Sciences (Singapore) Lecture Notes Series , 2006
Subdivision surfaces have become a standard geometric modeling tool for a variety of applications. This survey is an introduction to subdivision algorithms for arbitrary meshes and related mathematical theory; we review the most important subdivision schemes the theory of smoothness of subidivision surfaces, and known facts about approximation properties of subdivision bases.
[
Paper]
 Curvature-based energy for simulation
Curvature-based energy for simulation
Denis Zorin,
Shape Modeling International Proceedings , 2005
Curvature-based energy and forces are used in a broad variety of contexts, ranging from modeling of thin plates and shells to surface fairing and variational surface design. The approaches to discretization preferred in different areas often have little in common: engineering shell analysis is dominated by finite elements, while spring-particle models are often preferred for animation and qualitative simulation due to their simplicity and low computational cost. Both types of approaches have found applications in geometric modeling. While there is a well-established theory for finite element methods, alternative discretizations are less well understood: many questions about mesh dependence, convergence and accuracy remain unanswered. We discuss the general principles for defining curvaturebased energy on discrete surfaces based on geometric invariance and convergence considerations. We show how these principles can be used to understand the behavior of some commonly used discretizations, to establish relations between some well-known discrete geometry and finite element formulations and to derive new simple and efficient discretizations.
[
Paper]
 A survey of subdivision-based tools for surface modeling
A survey of subdivision-based tools for surface modeling
Ioana Boier-Martin,
Denis Zorin,
Fausto Bernardini,
AMS/DIMACS Volume on Computer-Aided Design and Manufacturing , 2005
Subdivision surfaces have emerged as a powerful representation for surface modeling and design. They address important limitations of traditional spline-based methods, such as the ability to handle arbitrary topologies and to support multiscale editing operations. In this paper we survey existing subdivision-based modeling methods with emphasis on interactive tools for styling and decoration of 3D models.
[
Paper]
 Interactive modeling of topologically complex geometric detail
Interactive modeling of topologically complex geometric detail
Jianbo Peng,
Daniel Kristjansson,
Denis Zorin,
ACM Transactions on Graphics (SIGGRAPH 2004 Proceedings), 2004
Volume textures aligned with a surface can be used to add topologically complex geometric detail to objects in an efficient way, while retaining an underlying simple surface structure. Adding a volume texture to a surface requires more than a conventional two-dimensional parameterization: a part of the space surrounding the surface has to be parameterized. Another problem with using volume textures for adding geometric detail is the difficulty in rendering implicitly represented surfaces, especially when they are changed interactively. In this paper we present algorithms for constructing and rendering volume-textured surfaces. We demonstrate a number of interactive operations that these algorithms enable.
[
Paper]
[
Video]
 A simple manifold-based construction of surfaces of arbitrary smoothness
A simple manifold-based construction of surfaces of arbitrary smoothness
Lexing Ying,
Denis Zorin,
ACM Transactions on Graphics (SIGGRAPH 2004 Proceedings), 2004
We present a smooth surface construction based on the manifold approach of Grimm and Hughes. We demonstrate how this approach can relatively easily produce a number of desirable properties which are hard to achieve simultaneously with polynomial patches, subdivision or variational surfaces. Our surfaces are C-infinity-continuous with explicit nonsingular C-infinity parameterizations, high-order flexible at control vertices, depend linearly on control points, have fixed-size local support for basis functions, and have good visual quality.
[
Paper]
 Differentiable parametrization of Catmull-Clark subdivision surfaces
Differentiable parametrization of Catmull-Clark subdivision surfaces
Ioana Boier-Martin,
Denis Zorin,
Eurographics/SIGGRAPH Symposium on Geometry Processing , 2004
Subdivision-based representations are recognized as important tools for the generation of high-quality surfaces for Computer Graphics. In this paper we describe two parameterizations of Catmull-Clark subdivision surfaces that allow a variety of algorithms designed for other types of parametric surfaces (i.e., B-splines) to be directly applied to subdivision surfaces. In contrast with the natural parameterization of subdivision surfaces characterized by diverging first order derivatives around extraordinary vertices of valence higher than four, the derivatives associated with our proposed methods are defined everywhere on the surface. This is especially important for Computer-Aided Design (CAD) applications that seek to address the limitations of NURBS-based representations through the more flexible subdivision framework.
[
Paper]
 Lofting curve networks using subdivision surfaces
Lofting curve networks using subdivision surfaces
Scott Schaefer,
Joe Warren,
Denis Zorin,
Eurographics/SIGGRAPH Symposium on Geometry Processing , 2004
Lofting is a traditional technique for creating a curved shape by first specifying a network of curves that approximates the desired shape and then interpolating these curves with a smooth surface. This paper addresses the problem of lofting from the viewpoint of subdivision. First, we develop a subdivision scheme for an arbitrary network of cubic B-splines capable of being interpolated by a smooth surface. Second, we provide a quadrangulation algorithm to construct the topology of the surface control mesh. Finally, we extend the Catmull-Clark scheme to produce surfaces that interpolate the given curve network. Near the curve network, these lofted subdivision surfaces are C2 bicubic splines, except for those points where three or more curves meet. We prove that the surface is C1 with bounded curvature at these points in the most common cases; empirical results suggest that the surface is also C1 in the general case.
[
Paper]
 A kernel-independent adaptive fast multipole algorithm in two and three dimensions
A kernel-independent adaptive fast multipole algorithm in two and three dimensions
Lexing Ying,
George Biros,
Denis Zorin,
Journal of Computational Physics , 2004
We present a new fast multipole method for particle simulations. The main feature of our algorithm is that it does not require the implementation of multipole expansions of the underlying kernel, and it is based only on kernel evaluations. Instead of using analytic expansions to represent the potential generated by sources inside a box of the hierarchical FMM tree. we use a continuous distribution of an equivalent density on a surface enclosing the box. To find this equivalent density, we match its potential to the potential of the original sources at a surface, in the far field, by solving local Dirichlet-type boundary value problems. The far-field evaluations are sparsified with singular value decomposition in 2D or fast Fourier transforms in 3D. We have tested the new method on the single and double layer operators for the Laplacian, the modified Laplacian, the Stokes, the modified Stokes, the Navier, and the modified Navier operators in two and three dimensions. Our numerical results indicate that our method compares very well with the best known implementations of the analytic FMM method for both the Laplacian and modified Laplacian kernels. Its advantage is the (relative) simplicity of the implementation and its immediate extension to more general kernels.
[
Paper]
[
Code]
 A discrete model for inelastic deformation of thin shells
A discrete model for inelastic deformation of thin shells
Adrian Secord,
Eitan Grinspun,
Denis Zorin,
Technical report (poster presented at SCA 2004), 2004
We introduce a method for simulating the inelastic deformation of thin shells: we model plasticity and fracture of curved, deformable objects such as light bulbs, egg-shells and bowls. Our novel approach uses triangle meshes yet evolves fracture lines unrestricted to mesh edges. We present a novel measure of bending strain expressed in terms of surface invariants such as lengths and angles. We also demonstrate simple techniques to improve the robustness of standard timestepping as well as collision response algorithms.
[
Paper]
 A new parallel kernel-independent fast multipole method
A new parallel kernel-independent fast multipole method
Lexing Ying,
George Biros,
M. Harper Langston,
Denis Zorin,
SC 2003: Proceedings of the 2003 ACM/IEEE conference on Supercomputing (Best student paper award, Gordon Bell prize finalist), 2003
We present a new adaptive fast multipole algorithm and its parallel implementation. The algorithm is kernel-independent in the sense that the evaluation of pairwise interactions does not rely on any analytic expansions, but only utilizes kernel evaluations. The new method provides the enabling technology for many important problems in computational science and engineering. Examples include viscous flows, fracture mechanics and screened Coulombic interactions. Our MPI-based parallel implementation logically separates the computation and communication phases to avoid synchronization in the upward and downward computation passes, and thus allows us to fully exploit computation and communication overlapping. We measure isogranular and fixed-size scalability for a variety of kernels on the Pittsburgh Supercomputing Center's TCS-1 Alphaserver on up to 3000 processors. We have solved viscous flow problems with up to 2.1 billion unknowns and we have achieved 1.6 Tflops/s peak performance and 1.13 Tflops/s sustained performance.
[
Paper]
 A fast solver for the Stokes equations with distributed forces in complex geometries
A fast solver for the Stokes equations with distributed forces in complex geometries
George Biros,
Lexing Ying,
Denis Zorin,
Journal of Computational Physics , 2003
We present a new method for the solution of the Stokes equations. The main features of our method are: (1) it can be applied to arbitrary geometries in a black-box fashion; (2) it is second-order accurate; and (3) it has optimal algorithmic complexity. Our approach, to which we refer as the embedded boundary integral method (EBI), is based on Anita Mayo's work for the Poisson's equation: 'The Fast Solution of Poisson's and the Biharmonic Equations on Irregular Regions', SIAM Journal on Numerical Analysis, 21 (1984) 285-299. We embed the domain in a rectangular domain, for which fast solvers are available, and we impose the boundary conditions as interface (jump) conditions on the velocities and tractions. We use an indirect boundary integral formulation for the homogeneous Stokes equations to compute the jumps. The resulting equations are discretized by Nystrom's method. The rectangular domain problem is discretized by finite elements for a velocity-pressure formulation with equal order interpolation bilinear elements (Q1-Q1). Stabilization is used to circumvent the inf-sup condition for the pressure space. For the integral equations, fast matrix-vector multiplications are achieved via an N log N algorithm based on a block representation of the discrete integral operator, combined with (kernel independent) singular value decomposition to sparsity low-rank blocks. The regular grid solver is a Krylov method (conjugate residuals) combined with an optimal two-level Schwartz-preconditioner. For the integral equation we use GMRES. We have tested our algorithm on several numerical examples and we have observed optimal convergence rates.
[
Paper]
 Sharp features on multiresolution subdivision surfaces
Sharp features on multiresolution subdivision surfaces
Henning Biermann,
Ioana Boier-Martin,
Fausto Bernardini,
Denis Zorin,
Graphical Models (Previously appeared in Proceedings of PG 2001), 2002
In this paper we describe a method for creating sharp features and trim regions on multiresolution subdivision surfaces along a set of user-defined curves. Operations such as engraving, embossing, and trimming are important in many surface modeling applications. Their implementation, however, is nontrivial due to computational, topological, and smoothness constraints that the underlying surface has to satisfy. The novelty of our work lies in the ability to create sharp features anywhere on a surface and in the fact that the resulting representation remains within the multiresolution subdivision framework. Preserving the original representation has the advantage that other operations applicable to multiresolution subdivision surfaces can subsequently be applied to the edited model. We also introduce an extended set of subdivision rules for Catmull-Clark surfaces that allows the creation of creases along diagonals of control mesh faces.
[
Paper]
 The embedded boundary integral method for the incompressible Navier-Stokes equations
The embedded boundary integral method for the incompressible Navier-Stokes equations
George Biros,
Lexing Ying,
Denis Zorin,
Proceedings of International Association for Boundary Element Methods 2002 Symposium , 2002
We present a new method for the solution of the unsteady incompressible Navier-Stokes equations. Our goal is to achieve a robust and scalable methodology for two and three dimensional incompressible flows. The discretization of the Navier-Stokes operator is done using boundary integrals and structured-grid finite elements. We use finite-differences to advance the equations in time. The convective term is discretized via a semi-Lagrangian formulation which not only results in a spatial constant-coefficient (modified) Stokes operator, but in addition is unconditionally stable. The Stokes operator is inverted by a double-layer boundary integral formulation. Domain integrals are computed via finite elements with appropriate forcing singularities to account for the irregular geometry. We use a velocity-pressure formulation which we discretize with bilinear elements (Q1-Q1), which give equal order interpolation for the velocities and pressures. Stabilization is used to circumvent the div-stability condition for the pressure space. The integral equations are discretized by Nystrom's method. For the specific approximation choices the method is second order accurate. Our code is built on top of PETSc, an MPI based parallel linear algebra library. We will present numerical results and discuss the performance and scalability of the method in two dimensions.
[
Paper]
 Cut-and-paste editing of multiresolution surfaces
Cut-and-paste editing of multiresolution surfaces
Henning Biermann,
Ioana Boier-Martin,
Fausto Bernardini,
Denis Zorin,
SIGGRAPH Proceedings , 2002
Cutting and pasting to combine different elements into a common structure are widely used operations that have been successfully adapted to many media types. Surface design could also benefit from the availability of a general, robust, and efficient cut-and-paste too], especially during the initial stages of design when a large space of alternatives needs to be explored. Techniques to support cut-and-paste operations for surfaces have been proposed in the past, but have been of limited usefulness due to constraints on the type of shapes supported and the lack of real-time interaction. In this paper, we describe a set of algorithms based on multiresolution subdivision surfaces that per-form at interactive rates and enable intuitive cut-and-paste operations.
[
Paper]
[
Video]
 Evaluation of piecewise smooth subdivision surfaces
Evaluation of piecewise smooth subdivision surfaces
Denis Zorin,
Daniel Kristjansson,
Visual Computer , 2002
In this paper we consider the constant-time evaluation of subdivision surfaces at arbitrary points. Our work extends the work of J. Stam by considering the subdivision rules for piecewise smooth surfaces with boundaries depending on parameters. The main innovation described in this paper is the idea of using a different set of basis vectors for evaluation, which, unlike eigenvectors, depend continuously on the coefficients of the subdivision rules. The advantage of this approach is that it becomes possible to define evaluation for parametric families of rules without considering an excessive number of special cases and while improving the numerical stability of calculations. We demonstrate how such bases are computed for a particular parametric family of subdivision rules extending Loop subdivision to meshes with boundaries, and we provide a detailed description of the evaluation algorithms.
[
Paper]
 Approximate boolean operations on free-form solids
Approximate boolean operations on free-form solids
Henning Biermann,
Daniel Kristjansson,
Denis Zorin,
SIGGRAPH 2001 Proceedings , 2001
In this paper we describe a method for computing approximate results of boolcan operations (union, intersection, difference) applied to free-form solids bounded by multiresolution subdivision surfaces. We present algorithms for generating a control mesh for a multiresolution surface approximating the result, optimizing the parameterization of the new surface with respect to the original surfaces, and fitting the new surface to the geometry of the original surfaces. Our algorithms aim to minimize the size and optimize the quality of the new control mesh. The original control meshes are modified only in a neighborhood of the intersection. While the main goal is to obtain approximate results, high-accuracy approximations are also possible at additional computational expense, if the topology of the intersection curve is resolved correctly.
[
Paper]
 Simple and efficient algorithm for surface denoising
Simple and efficient algorithm for surface denoising
Jianbo Peng,
Vasily Strela,
Denis Zorin,
IEEE Visualization 2001 Proceedings , 2001
We present a simple denoising technique for geometric data represented as a semiregular mesh, based on locally adaptive Wiener filtering. The degree of denoising is controlled by a single parameter (an estimate of the relative noise level) and the time required for denoising is independent of the magnitude of the estimate. The performance of the algorihm is sufficiently fast to allow interactive local denoising.
[
Paper]
[
Video]
 Nonmanifold subdivision
Nonmanifold subdivision
Lexing Ying,
Denis Zorin,
IEEE Visualization 2001 Proceedings , 2001
Commonly-used subdivision schemes require manifold control meshes and produce manifold surfaces. However, it is often necessary to model nonmanifold surfaces, such as several surface patches meeting at a common boundary.In this paper, we describe a subdivision algorithm that makes it possible to model nonmanifold surfaces. Any triangle mesh, subject only to the restriction that no two vertices of any triangle coincide, can serve as an input to the algorithm. Resulting surfaces consist of collections of manifold patches joined along nonmanifold curves and vertices. If desired, constraints may be imposed on the tangent planes of manifold patches sharing a curve or a vertex.The algorithm is an extension of a well-known Loop subdivision scheme, and uses techniques developed for piecewise smooth surfaces.
[
Paper]
 Texture and shape synthesis on surfaces
Texture and shape synthesis on surfaces
Lexing Ying,
Aaron Hertzmann,
Henning Biermann,
Denis Zorin,
Proceedings of 12th Eurographics Workshop on Rendering 2001 , 2001
We present a novel method for texture synthesis on surfaces from examples. We consider a very general type of textures, including color, transparency and displacements. Our method synthesizes the texture directly on the surface, rather than synthesizing a texture image and then mapping it to the surface. This approach avoids many problems associated with texture mapping, such as seams, distortion, and repeating patterns. The synthesized textures have the same qualitative visual appearance as the example texture, and cover the surfaces seamlessly, without distortion. We describe two synthesis methods, based on the work of Wei and Levoy and Ashikhmin; our techniques produce similar results but directly on surfaces.
[
Paper]
 4-8 subdivision
4-8 subdivision
Luiz Velho,
Denis Zorin,
Computer-Aided Geometric Design (Special Issue on Subdivision), 2001
In this paper we introduce 4-8 subdivision, a new scheme that generalizes the four-directional box spline of class C-4 to surfaces of arbitrary topological type. The crucial advantage of the proposed scheme is that it uses bisection refinement as an elementary refinement operation, rather than more commonly used face or vertex splits. In the uniform case, bisection refinement results in doubling, rather than quadrupling of the number of faces in a mesh. Adaptive bisection refinement automatically generates conforming variable-resolution meshes in contrast to face and vertex split methods which require a postprocessing step to make an adaptively refined mesh conforming. The fact that the size of faces decreases more gradually with refinement allows one to have greater control over the resolution of a refined mesh. It also makes it possible to achieve higher smoothness while using small stencils (the size of the stencils used by our scheme is similar to Loop subdivision). We show that the subdivision surfaces produced by the 4-8 scheme are C-4 continuous almost everywhere, except at extraordinary vertices where they are is C-1-continuous.
[
Paper]
 A Unified framework for primal/dual quadrilateral subdivision Schemes
A Unified framework for primal/dual quadrilateral subdivision Schemes
Denis Zorin,
Peter Schroeder,
Computer-Aided Geometric Design (Special Issue on Subdivision), 2001
Quadrilateral subdivision schemes come in primal and dual varieties, splitting faces or respectively vertices. The scheme of Catmull-Clark is an example of the former, while the Doo-Sabin scheme exemplifies the latter. In this paper we consider the construction of an increasing sequence of alternating primal/dual quadrilateral subdivision schemes based on a simple averaging approach. Beginning with a vertex split step we successively construct variants of Doo-Sabin and Catmull-Clark schemes followed by novel schemes generalizing B-splines of bidegree up to nine. We prove the schemes to be C-1 at irregular surface points, and analyze the behavior of the schemes as the number of averaging steps increases. We discuss a number of implementation issues common to all quadrilateral schemes. In particular we show how both primal and dual quadrilateral schemes can be implemented in the same code, opening up new possibilities for more flexible geometric modeling applications and p-versions of the Subdivision Element Method. Additionally we describe a simple algorithm for adaptive subdivision of dual schemes.
[
Paper]
 Piecewise smooth subdivision surfaces with boundary and normal control
Piecewise smooth subdivision surfaces with boundary and normal control
Henning Biermann,
Adi Levin,
Denis Zorin,
SIGGRAPH Proceedings , 2000
In this paper we introduce improved rules for Catmull-Clark and Loop subdivision that overcome several problems with the original schemes, namely, lack of smoothness at extraordinary boundary vertices and folds near concave corners. In addition, our approach to rule modification allows the generation of surfaces with prescribed normals, both on the boundary and in the interior, which considerably improves control of the shape of surfaces.
[
Paper]
[
Code]
 Artistic multi-projection images
Artistic multi-projection images
Maneesh Agrawala,
Denis Zorin,
Tamara Munzner,
Proceedings of 11th Eurographics Workshop on Rendering , 2000
In composing hand-drawn images of 3D scenes, artists often alter the projection for each object in the scene independently, thereby generating multiprojection images. We present a tool for creating such multiprojection images and animations, consisting of two parts: a multiprojection rendering algorithm and an interactive interface for attaching local cameras to the scene geometry. We describe a new set of techniques for resolving visibility between geometry rendered with different local cameras. We also develop several camera constraints that are useful when initially setting local camera parameters and when animating the scene. We demonstrate applications of our methods for generating a variety of artistic effects in still images and in animations.
[
Paper]
[
Video]
 Illustrating smooth surfaces
Illustrating smooth surfaces
Aaron Hertzmann,
Denis Zorin,
SIGGRAPH 2000 Proceedings , 2000
We present a new set of algorithms for line-art rendering of smooth surfaces. We introduce an efficient, deterministic algorithm for finding silhouettes based on geometric duality, and an algorithm for segmenting the silhouette curves into smooth parts with constant visibility. These methods can be used to find all silhouettes in real time in software. We present an automatic method for generating hatch marks in order to convey surface shape. We demonstrate these algorithms with a drawing style inspired by A Topological Picturebook by G. Francis.
[
Paper]
[
Code]
 A method for analysis of $C^1$-continuity of subdivision surfaces
A method for analysis of $C^1$-continuity of subdivision surfaces
Denis Zorin,
SIAM Journal of Numerical Analysis , 2000
A sufficient condition for C-1-continuity of subdivision surfaces was proposed by Reif [Comput. Aided Geom. Design, 12 (1995), pp. 153-174.] and extended to a more general setting in [Denis Zorin, Constr. Approx., accepted for publication]. In both cases, the analysis of C-1-continuity is reduced to establishing injectivity and regularity of a characteristic map. In all known proofs of C-1-continuity, explicit representation of the limit surface on an annular region was used to establish regularity, and a variety of relatively complex techniques were used to establish injectivity. We propose a new approach to this problem: we show that for a general class of subdivision schemes, regularity can be inferred from the properties of a sufficiently close linear approximation, and injectivity can be veri ed by computing the index of a curve. An additional advantage of our approach is that it allows us to prove C-1-continuity for all valences of vertices, rather than for an arbitrarily large but finite number of valences. As an application, we use our method to analyze C-1-continuity of most stationary subdivision schemes known to us, including interpolating butterfly and modified butterfly schemes, as well as the Kobbelt's interpolating scheme for quadrilateral meshes.
[
Paper]
 Smoothness of subdivision on irregular meshes
Smoothness of subdivision on irregular meshes
Denis Zorin,
Constructive Approximation , 2000
We derive necessary and sufficient conditions for tangent plane and C-k-continuity of stationary subdivision schemes near extraordinary vertices. Our criteria generalize most previously known conditions. We introduce a new approach to analysis of subdivision surfaces based on the idea of the universal surface. Any subdivision surface can be locally represented as a projection of the universal surface, which is uniquely defined by the subdivision scheme. This approach provides us with a more intuitive geometric understanding of subdivision near extraordinary vertices.
[
Paper]
 Subdivision for modeling and animation
Subdivision for modeling and animation
Denis Zorin,
Peter Schroeder,
Tony DeRose,
Leif Kobbelt,
Adi Levin,
Wim Sweldens,
SIGGRAPH 2000 Course Notes, (earlier version 1999) , 2000
This course provides an introduction to Subdivision, a technique to generate smooth curves and surfaces, which extends classical spline modeling approaches. The course will cover the basic ideas of subdivision as well as the particulars of a number of different subdivision algorithms; we will present the most recent contributions to the area in a form accessible to a wide audience. The emphasis will be on practical issues in using subdivision for geometric modeling and animation.
[
Link]
 Interactive multiresolution mesh editing
Interactive multiresolution mesh editing
Denis Zorin,
Peter Schroeder,
Wim Sweldens,
SIGGRAPH 1997 Proceedings , 1997
We describe a multiresolution representation for meshes based on subdivision,which is a natural extension of the existing patch-based surface representations. Combining subdivision and the smoothing algorithms of Taubin [26] allows us to construct a set of algorithms for interactive multiresolution editing of complex hierarchical meshes of arbitrary topology. The simplicity of the underlying algorithms for refinement and coarsification enables us to make them local and adaptive, thereby considerably improving their efficiency. We have built a scalable interactive multiresolution editing system based on such algorithms.
[
Paper]
[
Video 1]
[
Video 2]
[
Video 3]
[
Video 4]
[
Video 5]
 Interpolation subdivision for meshes of arbitrary topology
Interpolation subdivision for meshes of arbitrary topology
Denis Zorin,
Wim Sweldens,
Peter Schroeder,
SIGGRAPH 1996 Proceedings , 1996
Subdivision is a powerful paradigm for the generation of surfaces of arbitrary topology. Given an initial triangular mesh the goal is to produce a smooth and visually pleasing surface whose shape is controlled by the initialmesh. Of particular interest are interpolating schemes since they match the original data exactly, and play an important role in fast multiresolution and wavelet techniques. Dyn, Gregory, and Levin introduced the Butterfly scheme, which yields C1 surfaces in the topologically regular setting. Unfortunately it exhibits undesirable artifacts in the case of an irregular topology. We examine these failures and derive an improved scheme, which retains the simplicity of the Butterfly scheme, is interpolating, and results in smoother surfaces.
[
Paper]
[
Video]
 Correction of geometric perceptual distortion in pictures
Correction of geometric perceptual distortion in pictures
Denis Zorin,
Alan H. Barr,
SIGGRAPH 1995 Proceedings , 1995
We suggest an approach for correcting several types of perceived geometric distortions in computer-generated and photographic images. The approach is based on a mathematical formalization of desirable properties of pictures. From a small set of simple assumptions we obtain perceptually preferable viewing transformations and show that these transformations can be decomposed into a perspective or parallel projection followed by a planar transformation. The decomposition is easily implemented and provides a convenient framework for further analysis of the image mapping. We prove that two perceptually important properties are incompatible and cannot be satisfied simultaneously. It is impossible to construct a viewing transformation such that the images of all lines are straight and the images of all spheres are exact circles. Perceptually preferable tradeoffs between these two types of distortions can depend on the content of the picture. We construct parametric families of transformations with parameters representing the relative importance of the perceptual characteristics. By adjusting the settings of the parameters we canminimize the overall distortion of the picture. It turns out that a simple family of transformations produces results that are sufficiently close to optimal. We implement the proposed transformations and apply them to computer-generated and photographic perspective projection images. Our transformations can considerably reduce distortion in wide-angle motion pictures and computer-generated animations.
[
Paper]
[
Video]
 Symmetric constraints in classification problems that admit replacement by functional constraints
Symmetric constraints in classification problems that admit replacement by functional constraints
Denis Zorin,
Cybernetics and Systems Analysis , 1993
 On a connection between homogeneity and independence constraints for classification algorithms
On a connection between homogeneity and independence constraints for classification algorithms
Denis Zorin,
Cybernetics and Systems Analysis , 1991
We describe a set of functional universal constraints for classification algorithms that correspond to particular systems of symmetric universal constraints.
[
Paper]
[
Link]

 Solid-Shell Labeling for Discrete Surfaces
Solid-Shell Labeling for Discrete Surfaces
 High-Order Continuous Geometrical Validity
High-Order Continuous Geometrical Validity
 Feature-Aligned Parametrization in Penner Coordinates
Feature-Aligned Parametrization in Penner Coordinates
 Topological Offsets
Topological Offsets
 MiSo: A DSL for Robust and Efficient Solve and Minimize Problems
MiSo: A DSL for Robust and Efficient Solve and Minimize Problems
 Intersection-Free Garment Retargeting
Intersection-Free Garment Retargeting
 Geometric Contact Potential
Geometric Contact Potential
 Optimized shock-protecting microstructures
Optimized shock-protecting microstructures
 Cut-Cell Microstructures for Two-scale Structural Optimization
Cut-Cell Microstructures for Two-scale Structural Optimization
 Soft Pneumatic Actuator Design using Differentiable Simulation
Soft Pneumatic Actuator Design using Differentiable Simulation
 Differentiable solver for time-dependent deformation problems with contact
Differentiable solver for time-dependent deformation problems with contact
 Algebraic Smooth Occluding Contours
Algebraic Smooth Occluding Contours
 Bezier Spline Simplification Using Locally Integrated Error Metrics
Bezier Spline Simplification Using Locally Integrated Error Metrics
 High-Order Incremental Potential Contact for Elastodynamic Simulation on Curved Meshes
High-Order Incremental Potential Contact for Elastodynamic Simulation on Curved Meshes
 Declarative Specification for Unstructured Mesh Editing Algorithms
Declarative Specification for Unstructured Mesh Editing Algorithms
 A Cross-Platform Benchmark for Interval Computation Libraries
A Cross-Platform Benchmark for Interval Computation Libraries
 Which Cross Fields can be Quadrangulated? Global Parameterization from Prescribed Holonomy Signatures
Which Cross Fields can be Quadrangulated? Global Parameterization from Prescribed Holonomy Signatures
 DEF: Deep Estimation of Sharp Geometric Features in 3D Shapes
DEF: Deep Estimation of Sharp Geometric Features in 3D Shapes
 A Large Scale Comparison of Tetrahedral and Hexahedral Elements for Finite Element Analysis
A Large Scale Comparison of Tetrahedral and Hexahedral Elements for Finite Element Analysis
 A Large-Scale Benchmark for the Incompressible Navier-Stokes Equations
A Large-Scale Benchmark for the Incompressible Navier-Stokes Equations
 Hardware Design and Accurate Simulation for Benchmarking of 3D Reconstruction Algorithms
Hardware Design and Accurate Simulation for Benchmarking of 3D Reconstruction Algorithms
 Optimizing Contact-based Assemblies
Optimizing Contact-based Assemblies
 Efficient and Robust Discrete Conformal Equivalence with Boundary
Efficient and Robust Discrete Conformal Equivalence with Boundary
 An Extensible Benchmark Suite for Learning to Simulate Physical Systems
An Extensible Benchmark Suite for Learning to Simulate Physical Systems
 Intersection-free Rigid Body Dynamics
Intersection-free Rigid Body Dynamics
 Bijective and Coarse High-Order Tetrahedral Meshes
Bijective and Coarse High-Order Tetrahedral Meshes
 Orienting Point Clouds With Dipole Propagation
Orienting Point Clouds With Dipole Propagation
 Appearance-Preserving Tactile Optimization
Appearance-Preserving Tactile Optimization
 Bijective Projection in a Shell
Bijective Projection in a Shell
 A Low-Parametric Rhombic Microstructure Family for Irregular Lattices
A Low-Parametric Rhombic Microstructure Family for Irregular Lattices
 Fast Tetrahedral Meshing in the Wild
Fast Tetrahedral Meshing in the Wild
 Incremental Potential Contact: Intersection- and Inversion-free, Large-Deformation Dynamics
Incremental Potential Contact: Intersection- and Inversion-free, Large-Deformation Dynamics
 Reinforcement of General Shell Structures
Reinforcement of General Shell Structures
 A robust solver for elliptic PDEs in 3D complex geometries
A robust solver for elliptic PDEs in 3D complex geometries
 Scalable Simulation of Realistic Volume Fraction Red Blood Cell Flows through Vascular Networks
Scalable Simulation of Realistic Volume Fraction Red Blood Cell Flows through Vascular Networks
 Gradient Dynamics of Shallow Univariate ReLU Networks
Gradient Dynamics of Shallow Univariate ReLU Networks
 TriWild: Robust Triangulation with Curve Constraints
TriWild: Robust Triangulation with Curve Constraints
 Progressive Embedding
Progressive Embedding
 ABC: A Big CAD Model Dataset For Geometric Deep Learning
ABC: A Big CAD Model Dataset For Geometric Deep Learning
 Deep Geometric Prior for Surface Reconstruction
Deep Geometric Prior for Surface Reconstruction
 Parallel contact-aware simulations of deformable particles in 3D Stokes flow
Parallel contact-aware simulations of deformable particles in 3D Stokes flow
 Poly-Spline Finite Element Method
Poly-Spline Finite Element Method
 Quadrangulation of non-rigid objects using deformation metrics
Quadrangulation of non-rigid objects using deformation metrics
 Seamless Parametrization with Arbitrarily Prescribed Cones
Seamless Parametrization with Arbitrarily Prescribed Cones
 Decoupling Simulation Accuracy from Mesh Quality
Decoupling Simulation Accuracy from Mesh Quality
 Tetrahedral Meshing in the Wild
Tetrahedral Meshing in the Wild
 A Quantitative Perceptual Model for Tactile Roughness
A Quantitative Perceptual Model for Tactile Roughness
 A parameteric class of composites with a large achievable range of effective elastic properties
A parameteric class of composites with a large achievable range of effective elastic properties
 Tactile perception of the roughness of 3D-printed textures
Tactile perception of the roughness of 3D-printed textures
 Contact-aware simulations of particulate Stokesian suspensions
Contact-aware simulations of particulate Stokesian suspensions
 Worst-case stress relief for microstructures
Worst-case stress relief for microstructures
 Similarity maps and field-guided T-splines: a perfect couple
Similarity maps and field-guided T-splines: a perfect couple
 Surface Networks
Surface Networks
 On Discrete Conformal Seamless Similarity Maps
On Discrete Conformal Seamless Similarity Maps
 Ubiquitous evaluation of layer potentials using Quadrature by Kernel-Independent Expansion
Ubiquitous evaluation of layer potentials using Quadrature by Kernel-Independent Expansion
 Scale-Invariant Directional Alignment of Surface Parametrizations
Scale-Invariant Directional Alignment of Surface Parametrizations
 Interactive Modeling of Mechanical Objects
Interactive Modeling of Mechanical Objects
 A fast platform for simulating flexible fiber suspensions applied to cell mechanics
A fast platform for simulating flexible fiber suspensions applied to cell mechanics
 Bijective maps from simplicial foliations
Bijective maps from simplicial foliations
 Mesh Arrangements for Solid Geometry
Mesh Arrangements for Solid Geometry
 A Tensor-Train accelerated solver for integral equations in complex geometries
A Tensor-Train accelerated solver for integral equations in complex geometries
 Boundary Integral Method for the Flow of Vesicles with Viscosity Contrast in Three Dimensions
Boundary Integral Method for the Flow of Vesicles with Viscosity Contrast in Three Dimensions
 Elastic Textures
Elastic Textures
 Dyadic T-mesh subdivision
Dyadic T-mesh subdivision
 An O (N) direct solver for integral equations on the plane
An O (N) direct solver for integral equations on the plane
 Strict minimizers for geometric optimization
Strict minimizers for geometric optimization
 Smoothness of Subdivision Surfaces with Boundary
Smoothness of Subdivision Surfaces with Boundary
 Locally Injective Parametrization with Arbitrary Fixed Boundaries
Locally Injective Parametrization with Arbitrary Fixed Boundaries
 Robust Field-aligned Global Parametrization
Robust Field-aligned Global Parametrization
 Quad-Mesh Generation and Processing: A Survey
Quad-Mesh Generation and Processing: A Survey
 Subspace integration with local deformations
Subspace integration with local deformations
 Controlled-distortion constrained global parametrization
Controlled-distortion constrained global parametrization
 Worst-case structural analysis
Worst-case structural analysis
 A massively parallel adaptive fast multipole method on heterogeneous architectures
A massively parallel adaptive fast multipole method on heterogeneous architectures
 Fields on symmetric surfaces
Fields on symmetric surfaces
 Global parametrization by incremental flattening
Global parametrization by incremental flattening
 Computing extremal quasiconformal maps
Computing extremal quasiconformal maps
 Fields on Symmetric Surfaces
Fields on Symmetric Surfaces
 Global parametrization of range image sets
Global parametrization of range image sets
 Asynchronous integration with phantom meshes
Asynchronous integration with phantom meshes
 Manifold-based surfaces with boundary
Manifold-based surfaces with boundary
 A fast algorithm for simulating vesicle flows in three dimensions
A fast algorithm for simulating vesicle flows in three dimensions
 A Free-space adaptive FMM-Based PDE solver in three dimensions
A Free-space adaptive FMM-Based PDE solver in three dimensions
 Interference Aware Geometric Modeling
Interference Aware Geometric Modeling
 Petascale Direct Numerical Simulation of Blood Flow on 200K Cores and Heterogeneous Architectures.
Petascale Direct Numerical Simulation of Blood Flow on 200K Cores and Heterogeneous Architectures.
 Feature-aligned T-meshes
Feature-aligned T-meshes
 Mixed Finite Elements for Variational Surface Modeling
Mixed Finite Elements for Variational Surface Modeling
 Anisotropic quadrangulation
Anisotropic quadrangulation
 Real-time creased subdivision surfaces
Real-time creased subdivision surfaces
 A massively parallel adaptive fast-multipole method on heterogeneous architectures
A massively parallel adaptive fast-multipole method on heterogeneous architectures
 High-order methods for simulating the dynamics of axis-symmetric inextensible vesicles in viscous flow
High-order methods for simulating the dynamics of axis-symmetric inextensible vesicles in viscous flow
 Application-aware management of parallel simulation
Application-aware management of parallel simulation
 Structured annotations for 2D-to-3D modeling
Structured annotations for 2D-to-3D modeling
 A boundary integral method for simulating the dynamics of inextensible vesicles suspended in a viscous fluid in 2D
A boundary integral method for simulating the dynamics of inextensible vesicles suspended in a viscous fluid in 2D
 Shading-based surface editing
Shading-based surface editing
 Real-time rendering of textures with feature curves
Real-time rendering of textures with feature curves
 Result reuse in design space exploration: a study in system support for interactive parallel computing
Result reuse in design space exploration: a study in system support for interactive parallel computing
 Cubic shells
Cubic shells
 Shape optimization using reflection lines
Shape optimization using reflection lines
 Controlled-topology filtering
Controlled-topology filtering
 Discrete quadratic bending energies
Discrete quadratic bending energies
 Sim-X: Parallel system software for interactive multi-experiment computational studies
Sim-X: Parallel system software for interactive multi-experiment computational studies
 A High-order 3D boundary integral equation solver for elliptic PDEs in smooth domains
A High-order 3D boundary integral equation solver for elliptic PDEs in smooth domains
 A quadratic bending model for inextensible surfaces
A quadratic bending model for inextensible surfaces
 Constructing curvature-continuous surfaces by blending
Constructing curvature-continuous surfaces by blending
 Computing discrete shape operators on general meshes
Computing discrete shape operators on general meshes
 A Direct texture placement and editing interface
A Direct texture placement and editing interface
 Subdivision on arbitrary meshes: algorithms and theory
Subdivision on arbitrary meshes: algorithms and theory
 Curvature-based energy for simulation
Curvature-based energy for simulation
 A survey of subdivision-based tools for surface modeling
A survey of subdivision-based tools for surface modeling
 Interactive modeling of topologically complex geometric detail
Interactive modeling of topologically complex geometric detail
 A simple manifold-based construction of surfaces of arbitrary smoothness
A simple manifold-based construction of surfaces of arbitrary smoothness
 Differentiable parametrization of Catmull-Clark subdivision surfaces
Differentiable parametrization of Catmull-Clark subdivision surfaces
 Lofting curve networks using subdivision surfaces
Lofting curve networks using subdivision surfaces
 A kernel-independent adaptive fast multipole algorithm in two and three dimensions
A kernel-independent adaptive fast multipole algorithm in two and three dimensions
 A discrete model for inelastic deformation of thin shells
A discrete model for inelastic deformation of thin shells
 A new parallel kernel-independent fast multipole method
A new parallel kernel-independent fast multipole method
 A fast solver for the Stokes equations with distributed forces in complex geometries
A fast solver for the Stokes equations with distributed forces in complex geometries
 Sharp features on multiresolution subdivision surfaces
Sharp features on multiresolution subdivision surfaces
 The embedded boundary integral method for the incompressible Navier-Stokes equations
The embedded boundary integral method for the incompressible Navier-Stokes equations
 Cut-and-paste editing of multiresolution surfaces
Cut-and-paste editing of multiresolution surfaces
 Evaluation of piecewise smooth subdivision surfaces
Evaluation of piecewise smooth subdivision surfaces
 Approximate boolean operations on free-form solids
Approximate boolean operations on free-form solids
 Simple and efficient algorithm for surface denoising
Simple and efficient algorithm for surface denoising
 Nonmanifold subdivision
Nonmanifold subdivision
 Texture and shape synthesis on surfaces
Texture and shape synthesis on surfaces
 4-8 subdivision
4-8 subdivision
 A Unified framework for primal/dual quadrilateral subdivision Schemes
A Unified framework for primal/dual quadrilateral subdivision Schemes
 Piecewise smooth subdivision surfaces with boundary and normal control
Piecewise smooth subdivision surfaces with boundary and normal control
 Artistic multi-projection images
Artistic multi-projection images
 Illustrating smooth surfaces
Illustrating smooth surfaces
 A method for analysis of $C^1$-continuity of subdivision surfaces
A method for analysis of $C^1$-continuity of subdivision surfaces
 Smoothness of subdivision on irregular meshes
Smoothness of subdivision on irregular meshes
 Subdivision for modeling and animation
Subdivision for modeling and animation
 Interactive multiresolution mesh editing
Interactive multiresolution mesh editing
 Interpolation subdivision for meshes of arbitrary topology
Interpolation subdivision for meshes of arbitrary topology
 Correction of geometric perceptual distortion in pictures
Correction of geometric perceptual distortion in pictures
 Symmetric constraints in classification problems that admit replacement by functional constraints
Symmetric constraints in classification problems that admit replacement by functional constraints
 On a connection between homogeneity and independence constraints for classification algorithms
On a connection between homogeneity and independence constraints for classification algorithms