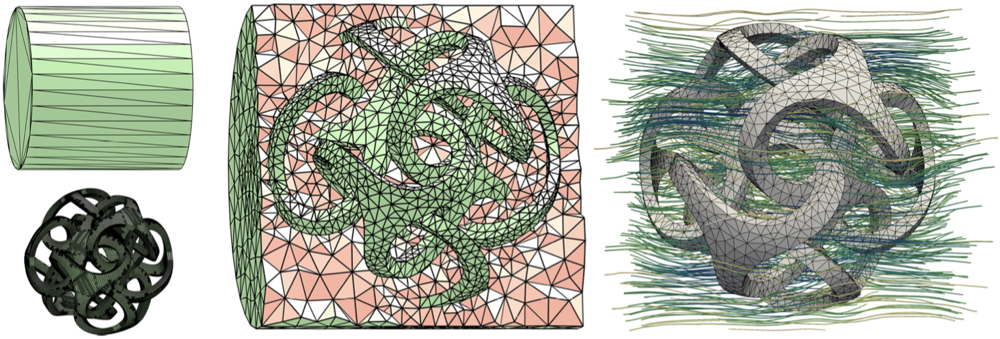
Black-Box Analysis: From Theory to Practice
The numerical solution of partial differential equations (PDEs) is ubiquitous in engineering applications, for the simulation of elastic deformations, fluids, and other physical phenomena. The finite element method (FEM) is the most commonly used discretization of PDEs due to its generality and rich selection of off-the-shelf commercial implementations. Ideally, a PDE solver should be a “black box”: the user provides as input the domain boundary, boundary conditions, and the governing equations, and the code returns an evaluator that can compute the value of the solution at any point of the input domain. This is surprisingly far from being the case for all existing open-source or commercial software, despite the research efforts in this direction and the large academic and industrial interest. To a large extent, this is due to treating meshing and FEM basis construction as two disjoint problems. The FEM basis construction may make a seemingly innocuous assumption (e.g., on the geometry of elements), that lead to exceedingly difficult requirements for meshing software. This state of matters presents a fundamental problem for applications that require fully automatic, robust processing of large collections of meshes of varying sizes, an increasingly common situation as large collections of geometric data become available. Most importantly, this situation arises in the context of machine learning on geometric and physical data, when one can run large numbers of simulations to learn from, as well as problems of shape optimization, which require solving PDEs in the inner optimization loop on a constantly changing domain. The first part of the course introduces the finite element method and recent advancements toward an integrated pipeline, considering meshing and element design as a single challenge, leading to a black-box pipeline that can solve simulations on 10 thousand in the wild meshes, without any parameter tuning. The second part demonstrates the effectiveness the black-box pipeline through practical examples in structural mechanics using state-of-the-art, easy-to-use, open-source Python libraries.

Geometric Computing with Python
Many disciplines of computer science have access to high level libraries allowing researchers and engineers to quickly produce prototypes. For instance, in machine learning, one can construct complex, state-of-the-art models which run on the GPU in a few lines of Python. In the field of geometric computing, however such high-level libraries are sparse. As a result, writing prototypes in geometry is time consuming and difficult even for advanced users. In this course, we present a set of easy-to-use Python packages for applications in geometric computing. We have designed these libraries to have a shallow learning curve, while also enabling programmers to easily accomplish a wide variety of complex tasks. Furthermore, the libraries we present share NumPy arrays as a common interface, making them highly composable with each-other as well as existing scientific computing packages. Finally, our libraries are blazing fast, doing most of the heavy computations in C++ with a minimal constant-overhead interface to Python. In the course, we will present a set of real-world examples from geometry processing, physical simulation, and geometric deep learning. Each example is prototypical of a common task in research or industry and is implemented in a few lines of code. By the end of the course, attendees will have exposure to a swiss-army-knife of simple, composable, and high-performance tools for geometric computing.
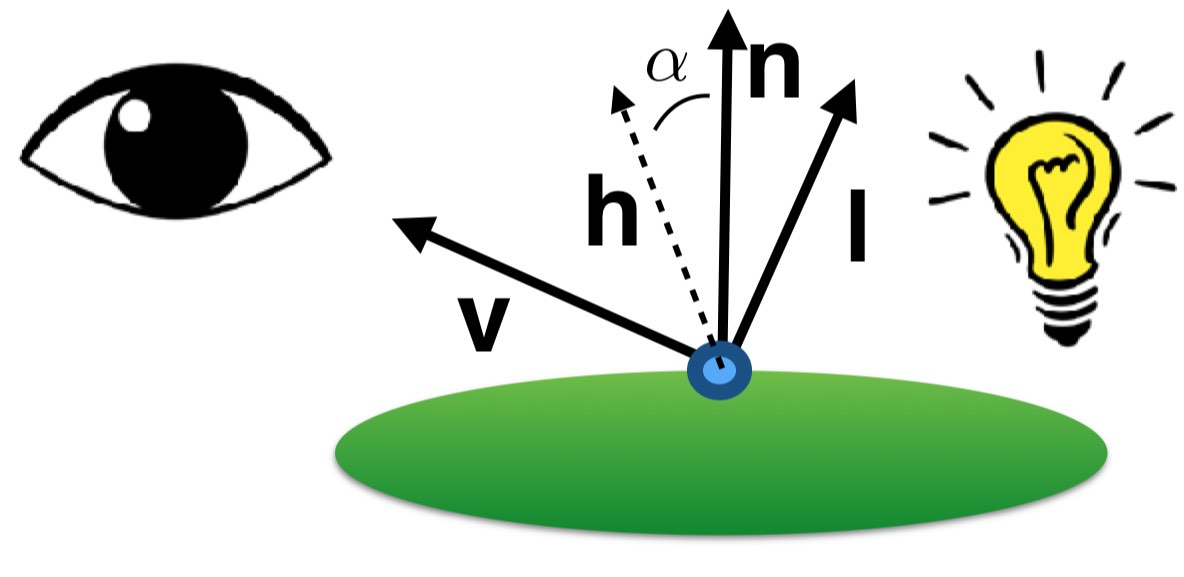
Computer Graphics - CSCI-GA.2270
This course provides an introduction to the field of Computer Graphics. We will cover the basic mathematical concepts, such as 2D and 3D transformations, study the interaction of light with geometry to derive shading models, and implement rendering algorithms such as ray tracing and rasterization. We will investigate how these fundamental components are integrated in current graphics processors and study the corresponding programming APIs. This course will also include a brief introduction to C++. Students will experiment with modern graphics programming and build small demos in C++ and OpenGL.
