Publications & Other Projects







Publications and Preprints
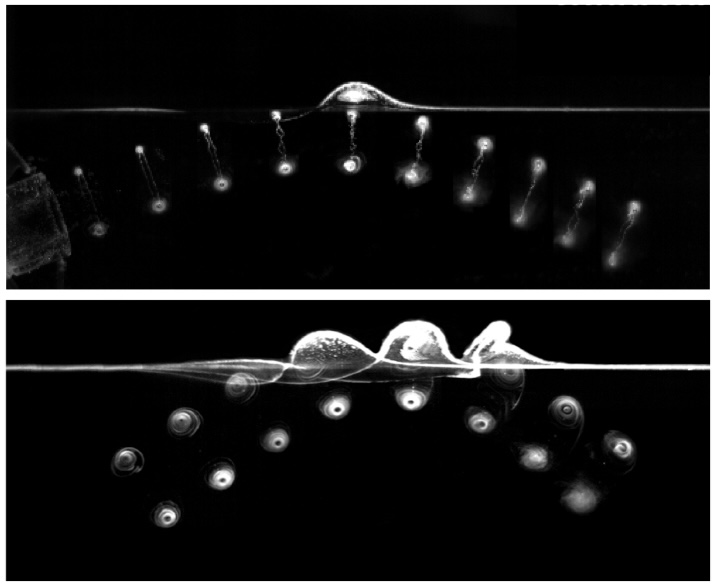
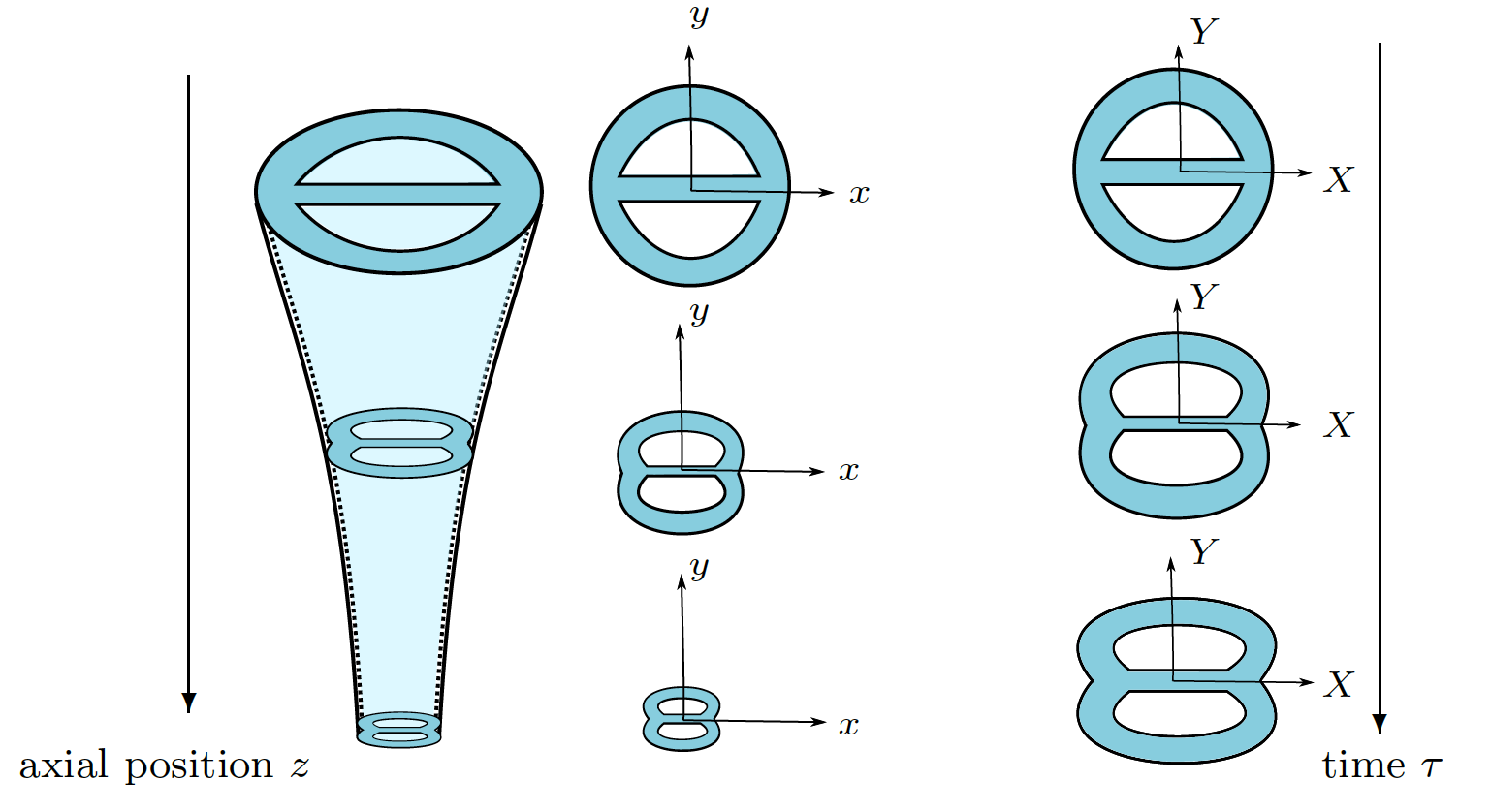
[14] Reflection of vortex rings at a water-air interface Journal, PDF
Z. Su, C. Mavroyiakoumou, J. Zhang, Phys. Rev. Fluids, 10, 074703 (2025)
We experimentally investigate how vortex rings, generated and propagating within a water tank, interact with the water-air interface. Near-perfect reflections of these vortex rings occur when they approach the interface at a sufficiently large incident angle. To understand this interaction, we employ a vortex-sheet-vortex-pair model in numerical simulations, which captures the essential dynamics. Additionally, a simplified model based on the conservation of flux or momentum provides further insight into the mechanism behind the vortex-ring reflection. Through combined approaches—experimentation, numerical simulation, and detailed analysis—we gain a deeper understanding of how vortex rings interact with free boundaries. Example movies showing a vortex ring reflection from experiments and simulations.
NYU News, Phys.org, Interesting Engineering, SRF, EurekAlert!, NYC Gazette
Z. Su, C. Mavroyiakoumou, J. Zhang, Phys. Rev. Fluids, 10, 074703 (2025)
We experimentally investigate how vortex rings, generated and propagating within a water tank, interact with the water-air interface. Near-perfect reflections of these vortex rings occur when they approach the interface at a sufficiently large incident angle. To understand this interaction, we employ a vortex-sheet-vortex-pair model in numerical simulations, which captures the essential dynamics. Additionally, a simplified model based on the conservation of flux or momentum provides further insight into the mechanism behind the vortex-ring reflection. Through combined approaches—experimentation, numerical simulation, and detailed analysis—we gain a deeper understanding of how vortex rings interact with free boundaries. Example movies showing a vortex ring reflection from experiments and simulations.
Other movies with an associated caption list are included in the Supplemental Material.
Some coverage: How Do Water Rings "Bounce"? New Discovery Answers Decades-Old QuestionNYU News, Phys.org, Interesting Engineering, SRF, EurekAlert!, NYC Gazette
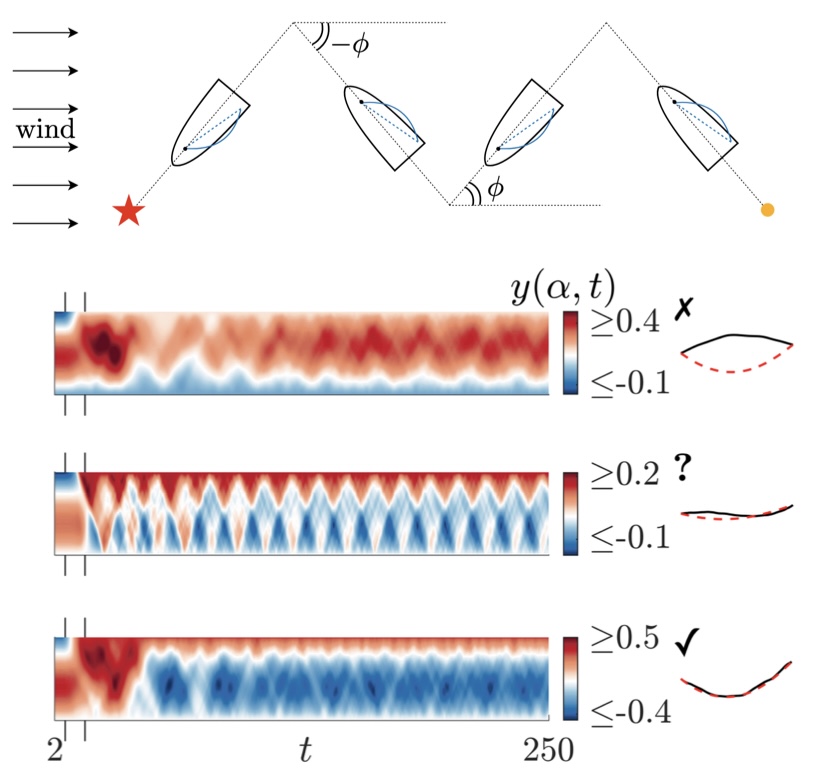
[13] Sail dynamics during tacking maneuvers Journal, arXiv *Editors' Suggestion*, *Featured in APS Physics Magazine*
C. Mavroyiakoumou, S. Alben, Phys. Rev. Fluids, 10, 073901 (2025)
We study the dynamics of sail membranes during a tacking maneuver, when the sail angle of attack is reversed in order to sail upwind. In successful tacking the sail flips to the mirror-image shape, while in unsuccessful tacking the sail remains stuck in a metastable state close to the initial shape. We investigate whether the sail flips, and if so, how long it takes and the subsequent dynamics, over a parameter space that describes the sail membrane properties and the kinematics of tacking. We find that the “steady” parameters—stretching rigidity, pretension, and final angle of attack—mostly determine whether a membrane flips or not. Flipping is more likely with larger values of the stretching rigidity, pretension, and final angle of attack. The dynamical parameters—membrane mass density, concavity of angle-of-attack transition kinematics, and time-length of the tacking maneuver—mainly affect how long flipping takes. With large membrane mass the membrane can maintain the momentum from the tacking motion long enough to reach the flipped state, but it may also take longer to converge to a steady shape. Concave-down angle-of-attack profiles and small tack times are generally associated with shorter flip times but a few exceptions exist, because these kinematics can also give a larger acceleration to the fluid-sail system that persists for longer times. We also investigate slack sails and find that they are more difficult to flip.
NYU News, Michigan News, Futurity, Phys.org, Ann Arbor Times, EurekAlert!, La Derniere Heure, Maroc Presse, The Mirage, NYC Gazette, Scuttlebutt Sailing News, tom's Hardware, Ars Technica, YouTube video
C. Mavroyiakoumou, S. Alben, Phys. Rev. Fluids, 10, 073901 (2025)
We study the dynamics of sail membranes during a tacking maneuver, when the sail angle of attack is reversed in order to sail upwind. In successful tacking the sail flips to the mirror-image shape, while in unsuccessful tacking the sail remains stuck in a metastable state close to the initial shape. We investigate whether the sail flips, and if so, how long it takes and the subsequent dynamics, over a parameter space that describes the sail membrane properties and the kinematics of tacking. We find that the “steady” parameters—stretching rigidity, pretension, and final angle of attack—mostly determine whether a membrane flips or not. Flipping is more likely with larger values of the stretching rigidity, pretension, and final angle of attack. The dynamical parameters—membrane mass density, concavity of angle-of-attack transition kinematics, and time-length of the tacking maneuver—mainly affect how long flipping takes. With large membrane mass the membrane can maintain the momentum from the tacking motion long enough to reach the flipped state, but it may also take longer to converge to a steady shape. Concave-down angle-of-attack profiles and small tack times are generally associated with shorter flip times but a few exceptions exist, because these kinematics can also give a larger acceleration to the fluid-sail system that persists for longer times. We also investigate slack sails and find that they are more difficult to flip.
Example movie. Other movies with an associated caption list can be found at this link.
Some coverage: New Study Tackles the Dynamics of Common—and Difficult—Sailing ManeuverNYU News, Michigan News, Futurity, Phys.org, Ann Arbor Times, EurekAlert!, La Derniere Heure, Maroc Presse, The Mirage, NYC Gazette, Scuttlebutt Sailing News, tom's Hardware, Ars Technica, YouTube video
Physics Magazine - How a Sail Inverts Its Shape
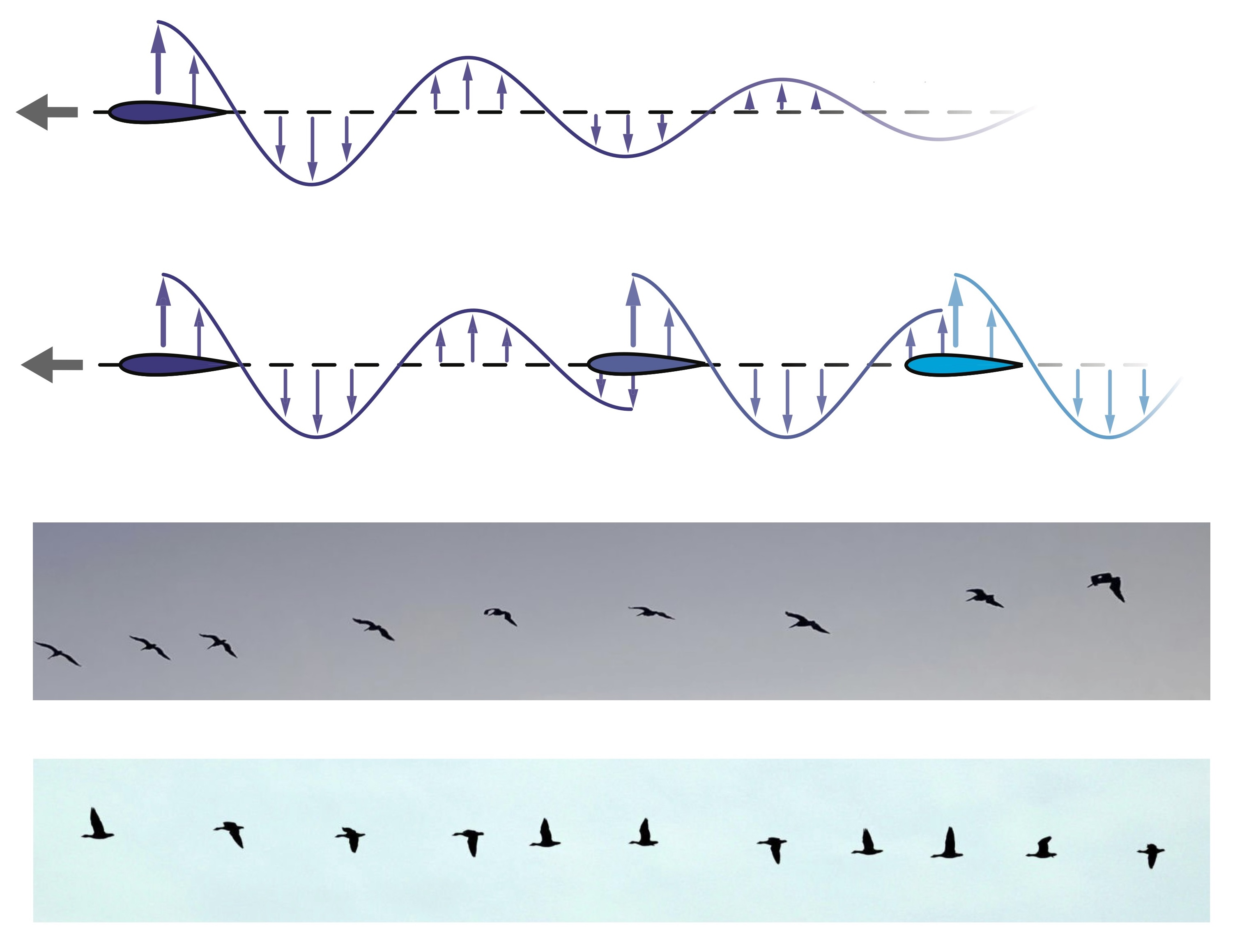
[12] Modeling flying formations as flow-mediated matter arXiv
C. Mavroyiakoumou, J. Wu, L. Ristroph (2025)
Collective locomotion of swimming and flying animals is fascinating in terms of individual-level fluid mechanics and group-level structure and dynamics. Here we bridge and relate these scales through a model of formation flight that views the collective as a material whose properties arise from the flow-mediated interactions among its members. We build on and revise an aerodynamic model describing how flapping flyers produce vortex wakes and how they are forced by others’ wakes. While simplistic, the model faithfully reproduces a series of physical experiments carried out over the last decade on pairwise interactions of flapping foils. By studying longer in-line arrays, we show that the group behaves as a soft "crystal" with regularly spaced member "atoms" whose positioning is, however, susceptible to deformations and dynamical instabilities. Poking or wiggling a member excites longitudinal waves (flow-mediated phonons, or "flonons") that pass down the group while growing in amplitude, and indeed the internal excitation from flapping is sufficient to trigger instabilities. Linear analysis of the model explains the aerodynamic origin of the lattice spacing, the springiness of the "bonds" between flyers, and the tendency for disturbances to resonantly amplify. Other properties such as the timescales for instability growth and wave propagation seem to involve the full nonlinear behavior. These findings suggest intriguing analogies with physical materials that could be generally useful for understanding and analyzing animal groups. Several properties displayed by our system seem particularly relevant to biological collectives, namely group cohesion and organization, sensitive detection of and response to perturbations, and transmission of information through traveling waves.
C. Mavroyiakoumou, J. Wu, L. Ristroph (2025)
Collective locomotion of swimming and flying animals is fascinating in terms of individual-level fluid mechanics and group-level structure and dynamics. Here we bridge and relate these scales through a model of formation flight that views the collective as a material whose properties arise from the flow-mediated interactions among its members. We build on and revise an aerodynamic model describing how flapping flyers produce vortex wakes and how they are forced by others’ wakes. While simplistic, the model faithfully reproduces a series of physical experiments carried out over the last decade on pairwise interactions of flapping foils. By studying longer in-line arrays, we show that the group behaves as a soft "crystal" with regularly spaced member "atoms" whose positioning is, however, susceptible to deformations and dynamical instabilities. Poking or wiggling a member excites longitudinal waves (flow-mediated phonons, or "flonons") that pass down the group while growing in amplitude, and indeed the internal excitation from flapping is sufficient to trigger instabilities. Linear analysis of the model explains the aerodynamic origin of the lattice spacing, the springiness of the "bonds" between flyers, and the tendency for disturbances to resonantly amplify. Other properties such as the timescales for instability growth and wave propagation seem to involve the full nonlinear behavior. These findings suggest intriguing analogies with physical materials that could be generally useful for understanding and analyzing animal groups. Several properties displayed by our system seem particularly relevant to biological collectives, namely group cohesion and organization, sensitive detection of and response to perturbations, and transmission of information through traveling waves.
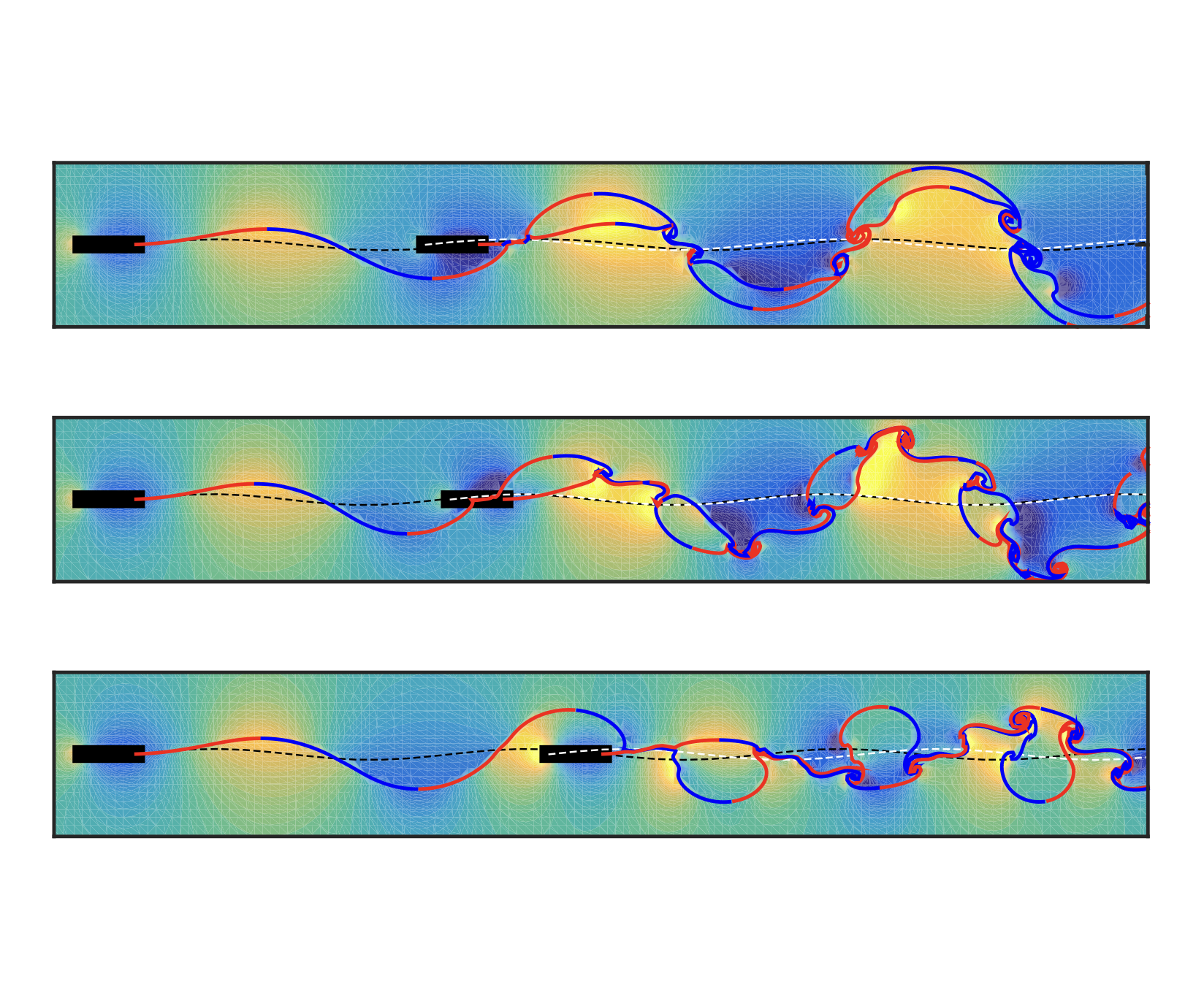
[11] Flow interactions and forward flight dynamics of tandem flapping wings arXiv
F. Fang, C. Mavroyiakoumou, L. Ristroph, M.J. Shelley (2025)
We examine theoretically the flow interactions and forward flight dynamics of tandem or in-line flapping wings. Two wings are driven vertically with prescribed heaving-and-plunging motions, and the horizontal propulsion speeds and positions are dynamically selected through aero- or hydro-dynamic interactions. Our simulations employ an improved vortex sheet method to solve for the locomotion of the pair within the collective flow field, and we identify 'schooling states' in which the wings travel together with nearly constant separation. Multiple terminal configurations are achieved by varying the initial conditions, and the emergent separations are approximately integer multiples of the wavelength traced out by each wing. We explain the stability of these states by perturbing the follower and mapping out an effective potential for its position in the leader's wake. Each equilibrium position is stabilized since smaller separations are associated with in-phase follower-wake motions that constructively reinforce the flow but lead to decreased thrust on the follower; larger separations are associated with antagonistic follower-wake motions, increased thrust, and a weakened collective wake. The equilibria and their stability are also corroborated by a linearized theory for the motion of the leader, the wake it produces, and its effect on the follower. We also consider a weakly-flapping follower driven with lower heaving amplitude than the leader. We identify 'keep-up' conditions for which the wings may still 'school' together despite their dissimilar kinematics, with the 'freeloading' follower passively assuming a favorable position within the wake that permits it to travel significantly faster than it would in isolation.
F. Fang, C. Mavroyiakoumou, L. Ristroph, M.J. Shelley (2025)
We examine theoretically the flow interactions and forward flight dynamics of tandem or in-line flapping wings. Two wings are driven vertically with prescribed heaving-and-plunging motions, and the horizontal propulsion speeds and positions are dynamically selected through aero- or hydro-dynamic interactions. Our simulations employ an improved vortex sheet method to solve for the locomotion of the pair within the collective flow field, and we identify 'schooling states' in which the wings travel together with nearly constant separation. Multiple terminal configurations are achieved by varying the initial conditions, and the emergent separations are approximately integer multiples of the wavelength traced out by each wing. We explain the stability of these states by perturbing the follower and mapping out an effective potential for its position in the leader's wake. Each equilibrium position is stabilized since smaller separations are associated with in-phase follower-wake motions that constructively reinforce the flow but lead to decreased thrust on the follower; larger separations are associated with antagonistic follower-wake motions, increased thrust, and a weakened collective wake. The equilibria and their stability are also corroborated by a linearized theory for the motion of the leader, the wake it produces, and its effect on the follower. We also consider a weakly-flapping follower driven with lower heaving amplitude than the leader. We identify 'keep-up' conditions for which the wings may still 'school' together despite their dissimilar kinematics, with the 'freeloading' follower passively assuming a favorable position within the wake that permits it to travel significantly faster than it would in isolation.
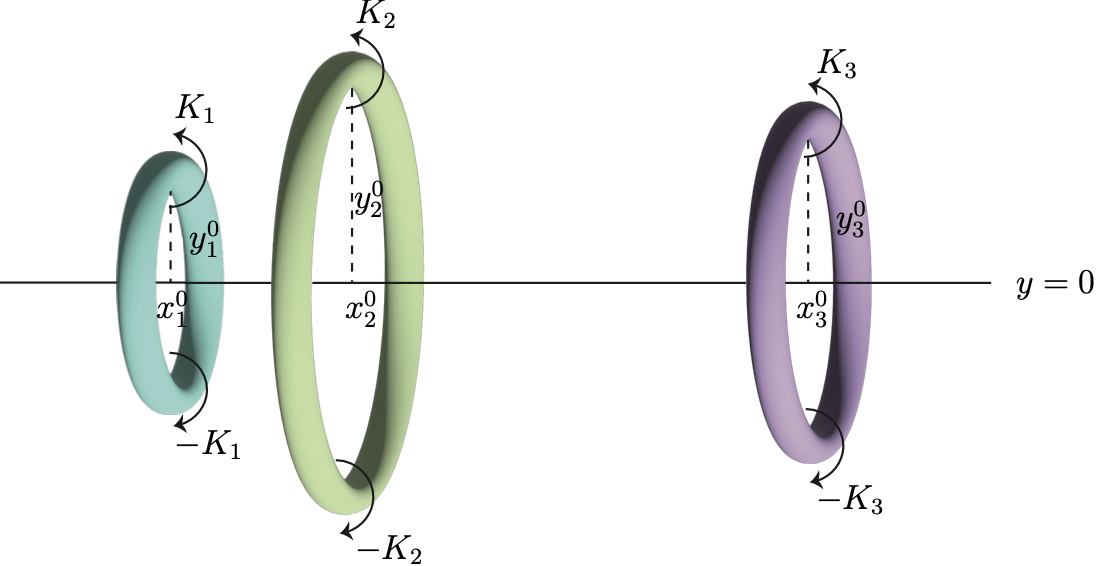
[10] Order and chaos in systems of two and three coaxial vortex pairs Journal, arXiv
C. Mavroyiakoumou, W. Shi, Physica D: Nonlinear Phenomema, Volume 481, 134767 (2025)
Systems of coaxial vortex pairs in an inviscid flow give rise to complex dynamics, with motions ranging from ordered to chaotic. This complexity arises due to the problem's high nonlinearity and numerous degrees of freedom. We analyze the periodic interactions of two vortex pairs with the same absolute strength moving along the same axis and in the same direction. We derive an explicit formula for the leapfrogging period, considering different initial sizes and horizontal separations, and find excellent quantitative agreement with the numerically computed leapfrogging period. We then extend our study to three coaxial vortex pairs with differing strengths, exploring a broad range of initial geometric configurations, and identify conditions that lead to escape to infinity, periodic or quasi-periodic leapfrogging, and chaotic interactions. We also quantify the occurrence of periodic leapfrogging, revealing that the system transitions to two subsystems when vortex pairs have dissimilar strengths and sizes. By performing a sensitivity analysis using neural networks, we find that the initial horizontal separation between the vortex pairs has the most significant effect on the leapfrogging period.
C. Mavroyiakoumou, W. Shi, Physica D: Nonlinear Phenomema, Volume 481, 134767 (2025)
Systems of coaxial vortex pairs in an inviscid flow give rise to complex dynamics, with motions ranging from ordered to chaotic. This complexity arises due to the problem's high nonlinearity and numerous degrees of freedom. We analyze the periodic interactions of two vortex pairs with the same absolute strength moving along the same axis and in the same direction. We derive an explicit formula for the leapfrogging period, considering different initial sizes and horizontal separations, and find excellent quantitative agreement with the numerically computed leapfrogging period. We then extend our study to three coaxial vortex pairs with differing strengths, exploring a broad range of initial geometric configurations, and identify conditions that lead to escape to infinity, periodic or quasi-periodic leapfrogging, and chaotic interactions. We also quantify the occurrence of periodic leapfrogging, revealing that the system transitions to two subsystems when vortex pairs have dissimilar strengths and sizes. By performing a sensitivity analysis using neural networks, we find that the initial horizontal separation between the vortex pairs has the most significant effect on the leapfrogging period.
[9] Flow interactions lead to self-organized flight formations disrupted by self-amplifying waves Journal, PDF
J. W. Newbolt, N. Lewis, M. Bleu, J. Wu, C. Mavroyiakoumou, S. Ramananarivo, L. Ristroph, Nature Communications, 15, 3462 (2024)
Collectively locomoting animals are often viewed as analogous to states of matter in that group-level phenomena emerge from individual-level interactions. Applying this framework to fish schools and bird flocks must account for visco-inertial flows as mediators of the physical interactions. Motivated by linear flight formations, here we show that pairwise flow interactions tend to promote crystalline or lattice-like arrangements, but such order is disrupted by unstably growing positional waves. Using robotic experiments on "mock flocks" of flapping wings in forward flight, we find that followers tend to lock into position behind a leader, but larger groups display flow-induced oscillatory modes—"flonons"—that grow in amplitude down the group and cause collisions. Force measurements and applied perturbations inform a wake interaction model that explains the self-ordering as mediated by spring-like forces and the self-amplification of disturbances as a resonance cascade. We further show that larger groups may be stabilized by introducing variability among individuals, which induces positional disorder while suppressing flonon amplification. These results derive from generic features including locomotor-flow phasing and nonreciprocal interactions with memory, and hence these phenomena may arise more generally in macroscale, flow-mediated collectives.
NYU News, Phys.org, ScienceDaily, EurekAlert!, The Mirage
J. W. Newbolt, N. Lewis, M. Bleu, J. Wu, C. Mavroyiakoumou, S. Ramananarivo, L. Ristroph, Nature Communications, 15, 3462 (2024)
Collectively locomoting animals are often viewed as analogous to states of matter in that group-level phenomena emerge from individual-level interactions. Applying this framework to fish schools and bird flocks must account for visco-inertial flows as mediators of the physical interactions. Motivated by linear flight formations, here we show that pairwise flow interactions tend to promote crystalline or lattice-like arrangements, but such order is disrupted by unstably growing positional waves. Using robotic experiments on "mock flocks" of flapping wings in forward flight, we find that followers tend to lock into position behind a leader, but larger groups display flow-induced oscillatory modes—"flonons"—that grow in amplitude down the group and cause collisions. Force measurements and applied perturbations inform a wake interaction model that explains the self-ordering as mediated by spring-like forces and the self-amplification of disturbances as a resonance cascade. We further show that larger groups may be stabilized by introducing variability among individuals, which induces positional disorder while suppressing flonon amplification. These results derive from generic features including locomotor-flow phasing and nonreciprocal interactions with memory, and hence these phenomena may arise more generally in macroscale, flow-mediated collectives.
Movie: Group of 30 flyers with AC perturbation on leading flyer
Some coverage: How Do Birds Flock? Researchers Do the Math to Reveal Previously Unknown Aerodynamic PhenomenonNYU News, Phys.org, ScienceDaily, EurekAlert!, The Mirage
[8] Spanwise variations in membrane flutter dynamics Journal, arXiv
C. Mavroyiakoumou, S. Alben, J. Fluids Struct., 130, 104194 (2024)
We study the large-amplitude flutter of rectangular membranes in 3-D inviscid flows, focusing on cases where the deflections have significant spanwise nonuniformity. We determine when such cases occur and how the dynamics vary over the parameter space of membrane mass and pretension for two sets of boundary conditions and two values of both the Poisson ratio and the membrane aspect ratio. With spanwise symmetric and asymmetric initial perturbations, the motions differ for long times but eventually reach the same steady state in most cases. At large times, spanwise symmetric and asymmetric oscillations are seen, with the latter more common. Oscillations are often in the form of "side-to-side" and other standing wave motions along the span, as well as traveling wave motions, particularly with free side-edges. Motions are generally nonperiodic and more spatially complex with a large membrane mass, and sometimes periodic at small-to-moderate membrane mass. A large Poisson ratio gives somewhat smoother spatial and temporal features in the dynamics at a given pretension. Increasing the aspect ratio makes the membrane "flatter," i.e. decreases spanwise variations in the deflection. With different chordwise and spanwise pretensions we find motions that are qualitatively similar to cases with isotropic pretensions between the anisotropic values. Movies with an associated caption list can be found at this link.
C. Mavroyiakoumou, S. Alben, J. Fluids Struct., 130, 104194 (2024)
We study the large-amplitude flutter of rectangular membranes in 3-D inviscid flows, focusing on cases where the deflections have significant spanwise nonuniformity. We determine when such cases occur and how the dynamics vary over the parameter space of membrane mass and pretension for two sets of boundary conditions and two values of both the Poisson ratio and the membrane aspect ratio. With spanwise symmetric and asymmetric initial perturbations, the motions differ for long times but eventually reach the same steady state in most cases. At large times, spanwise symmetric and asymmetric oscillations are seen, with the latter more common. Oscillations are often in the form of "side-to-side" and other standing wave motions along the span, as well as traveling wave motions, particularly with free side-edges. Motions are generally nonperiodic and more spatially complex with a large membrane mass, and sometimes periodic at small-to-moderate membrane mass. A large Poisson ratio gives somewhat smoother spatial and temporal features in the dynamics at a given pretension. Increasing the aspect ratio makes the membrane "flatter," i.e. decreases spanwise variations in the deflection. With different chordwise and spanwise pretensions we find motions that are qualitatively similar to cases with isotropic pretensions between the anisotropic values. Movies with an associated caption list can be found at this link.
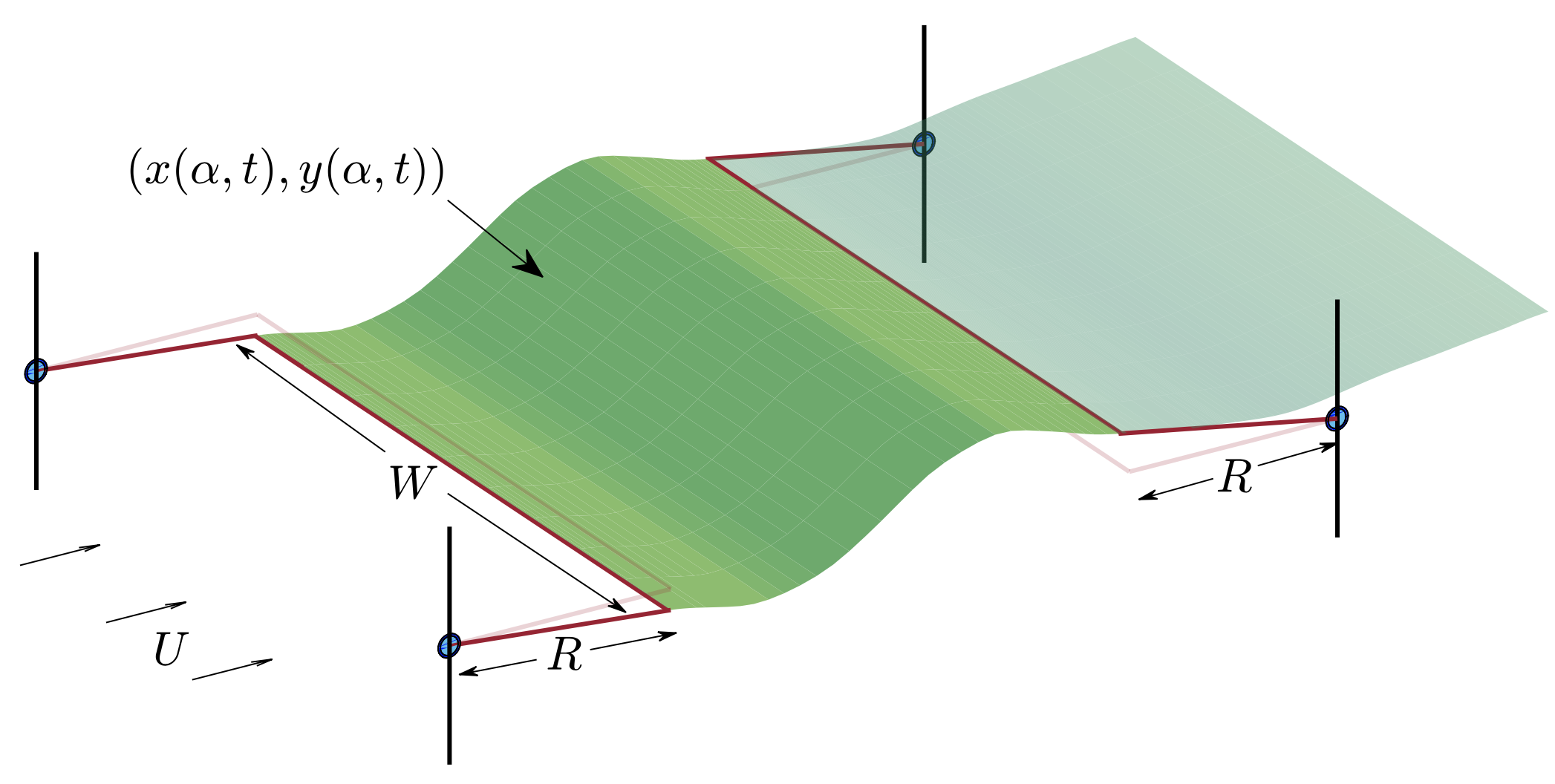
[7] Membrane flutter in three-dimensional inviscid flow Journal, arXiv
C. Mavroyiakoumou, S. Alben, Journal of Fluid Mechanics, 953, A32-1--38 (2022)
We develop a model and numerical method to study the large-amplitude flutter of rectangular membranes (of zero bending rigidity) that shed a trailing vortex-sheet wake in a three-dimensional (3D) inviscid fluid flow. We apply small initial perturbations and track their decay or growth to large-amplitude steady state motions. For 12 combinations of boundary conditions at the membrane edges we compute the stability thresholds and the subsequent large-amplitude dynamics across the three-parameter space of membrane mass density, pretension, and stretching rigidity. With free side edges we find good agreement with previous 2D results that used different discretization methods. We find that the 3D dynamics in the 12 cases leading and trailing edges. The deflection amplitudes and oscillation frequencies have scalings similar to those in the 2D case. The conditions at the side edges, though generally less important, may have small or large qualitative effects on the membrane dynamics—e.g. steady versus unsteady, periodic versus chaotic, or the variety of spanwise curvature distributions—depending on the group and the physical parameter values. Movies: [Movie Caption List]
Membrane boundary conditions: fixed-fixed: # 1, fixed-free: # 2, free-fixed: # 3, # 4, # 5, free-free: # 6, # 7, # 8, # 9, # 10
C. Mavroyiakoumou, S. Alben, Journal of Fluid Mechanics, 953, A32-1--38 (2022)
We develop a model and numerical method to study the large-amplitude flutter of rectangular membranes (of zero bending rigidity) that shed a trailing vortex-sheet wake in a three-dimensional (3D) inviscid fluid flow. We apply small initial perturbations and track their decay or growth to large-amplitude steady state motions. For 12 combinations of boundary conditions at the membrane edges we compute the stability thresholds and the subsequent large-amplitude dynamics across the three-parameter space of membrane mass density, pretension, and stretching rigidity. With free side edges we find good agreement with previous 2D results that used different discretization methods. We find that the 3D dynamics in the 12 cases leading and trailing edges. The deflection amplitudes and oscillation frequencies have scalings similar to those in the 2D case. The conditions at the side edges, though generally less important, may have small or large qualitative effects on the membrane dynamics—e.g. steady versus unsteady, periodic versus chaotic, or the variety of spanwise curvature distributions—depending on the group and the physical parameter values. Movies: [Movie Caption List]
Membrane boundary conditions: fixed-fixed: # 1, fixed-free: # 2, free-fixed: # 3, # 4, # 5, free-free: # 6, # 7, # 8, # 9, # 10
[6] Dynamics of tethered membranes in inviscid flow Journal, arXiv
C. Mavroyiakoumou, S. Alben, J. Fluids Struct., 107:103384 (2021)
We investigate the dynamics of membranes that are held by freely-rotating tethers in fluid flows. The tethered boundary condition allows periodic and chaotic oscillatory motions for certain parameter values. We characterize the oscillations in terms of deflection amplitudes, dominant periods, and numbers of deflection extrema along the membranes across the parameter space of membrane mass density, stretching modulus, pretension, and tether length. We determine the region of instability and the small-amplitude behavior by solving a nonlinear eigenvalue problem. We also consider an infinite periodic membrane model, which yields a regular eigenvalue problem, analytical results, and asymptotic scaling laws. We find qualitative similarities among all three models in terms of the oscillation frequencies and membrane shapes at small and large values of membrane mass, pretension, and tether length/stiffness.
C. Mavroyiakoumou, S. Alben, J. Fluids Struct., 107:103384 (2021)
We investigate the dynamics of membranes that are held by freely-rotating tethers in fluid flows. The tethered boundary condition allows periodic and chaotic oscillatory motions for certain parameter values. We characterize the oscillations in terms of deflection amplitudes, dominant periods, and numbers of deflection extrema along the membranes across the parameter space of membrane mass density, stretching modulus, pretension, and tether length. We determine the region of instability and the small-amplitude behavior by solving a nonlinear eigenvalue problem. We also consider an infinite periodic membrane model, which yields a regular eigenvalue problem, analytical results, and asymptotic scaling laws. We find qualitative similarities among all three models in terms of the oscillation frequencies and membrane shapes at small and large values of membrane mass, pretension, and tether length/stiffness.
[5] Eigenmode analysis of membrane stability in inviscid flow Journal, arXiv
C. Mavroyiakoumou, S. Alben, Phys. Rev. Fluids, 6, 043901-1--32 (2021)
We study the stability of a thin membrane (of zero bending rigidity) with a vortex sheet as a nonlinear eigenvalue problem in the parameter space of membrane mass (R1) and pretension (T0). With both ends fixed light membranes become unstable by a divergence instability and heavy membranes lose stability by flutter and divergence for a T0 that increases with R1. With the leading edge fixed and trailing edge free, or both edges free, membrane eigenmodes transition in shape across the stability boundary. We find good quantitative agreement with unsteady time-stepping simulations at small amplitude, but only qualitative similarities with the eventual steady-state large-amplitude motions.
C. Mavroyiakoumou, S. Alben, Phys. Rev. Fluids, 6, 043901-1--32 (2021)
We study the stability of a thin membrane (of zero bending rigidity) with a vortex sheet as a nonlinear eigenvalue problem in the parameter space of membrane mass (R1) and pretension (T0). With both ends fixed light membranes become unstable by a divergence instability and heavy membranes lose stability by flutter and divergence for a T0 that increases with R1. With the leading edge fixed and trailing edge free, or both edges free, membrane eigenmodes transition in shape across the stability boundary. We find good quantitative agreement with unsteady time-stepping simulations at small amplitude, but only qualitative similarities with the eventual steady-state large-amplitude motions.
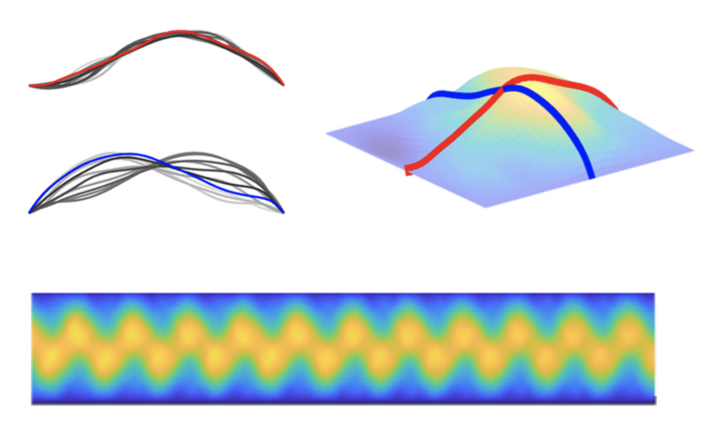
[4] Large-amplitude membrane flutter in inviscid flow Journal, arXiv
C. Mavroyiakoumou, S. Alben, Journal of Fluid Mechanics, 891, A23-1--34 (2020)
We study the large-amplitude flutter of membranes (of zero bending rigidity) with vortex sheet wakes in two-dimensional inviscid fluid flows. We apply small initial deflections and track their exponential decay or growth and subsequent large-amplitude dynamics in the space of three dimensionless parameters: membrane pretension, mass density and stretching modulus. With both ends fixed, all the membranes converge to steady deflected shapes with single humps that are nearly fore-aft symmetric, except when the deformations are unrealistically large. With leading edges fixed and trailing edges free to move in the transverse direction, the membranes flutter periodically at intermediate values of mass density. As mass density increases, the motions are increasingly aperiodic, and the amplitudes increase and spatial and temporal frequencies decrease. As mass density decreases from the periodic regime, the amplitudes decrease and spatial and temporal frequencies increase until the motions become difficult to resolve numerically. With both edges free to move in the transverse direction, the membranes flutter similarly to the fixed–free case, but also translate vertically with steady, periodic or aperiodic trajectories, and with non-zero slopes that lead to small angles of attack with respect to the oncoming flow. Movies:
Fixed-free membranes: (R1, R3, T0) = (10-0.5, 100.5, 10-2), (100, 100.5, 10-2), (100, 101, 10-2)
Free-free membranes: (R1, R3, T0) = (10-0.5, 100.5, 10-2), (100, 101, 10-2), (100.5, 101, 10-2)
C. Mavroyiakoumou, S. Alben, Journal of Fluid Mechanics, 891, A23-1--34 (2020)
We study the large-amplitude flutter of membranes (of zero bending rigidity) with vortex sheet wakes in two-dimensional inviscid fluid flows. We apply small initial deflections and track their exponential decay or growth and subsequent large-amplitude dynamics in the space of three dimensionless parameters: membrane pretension, mass density and stretching modulus. With both ends fixed, all the membranes converge to steady deflected shapes with single humps that are nearly fore-aft symmetric, except when the deformations are unrealistically large. With leading edges fixed and trailing edges free to move in the transverse direction, the membranes flutter periodically at intermediate values of mass density. As mass density increases, the motions are increasingly aperiodic, and the amplitudes increase and spatial and temporal frequencies decrease. As mass density decreases from the periodic regime, the amplitudes decrease and spatial and temporal frequencies increase until the motions become difficult to resolve numerically. With both edges free to move in the transverse direction, the membranes flutter similarly to the fixed–free case, but also translate vertically with steady, periodic or aperiodic trajectories, and with non-zero slopes that lead to small angles of attack with respect to the oncoming flow. Movies:
Fixed-free membranes: (R1, R3, T0) = (10-0.5, 100.5, 10-2), (100, 100.5, 10-2), (100, 101, 10-2)
Free-free membranes: (R1, R3, T0) = (10-0.5, 100.5, 10-2), (100, 101, 10-2), (100.5, 101, 10-2)
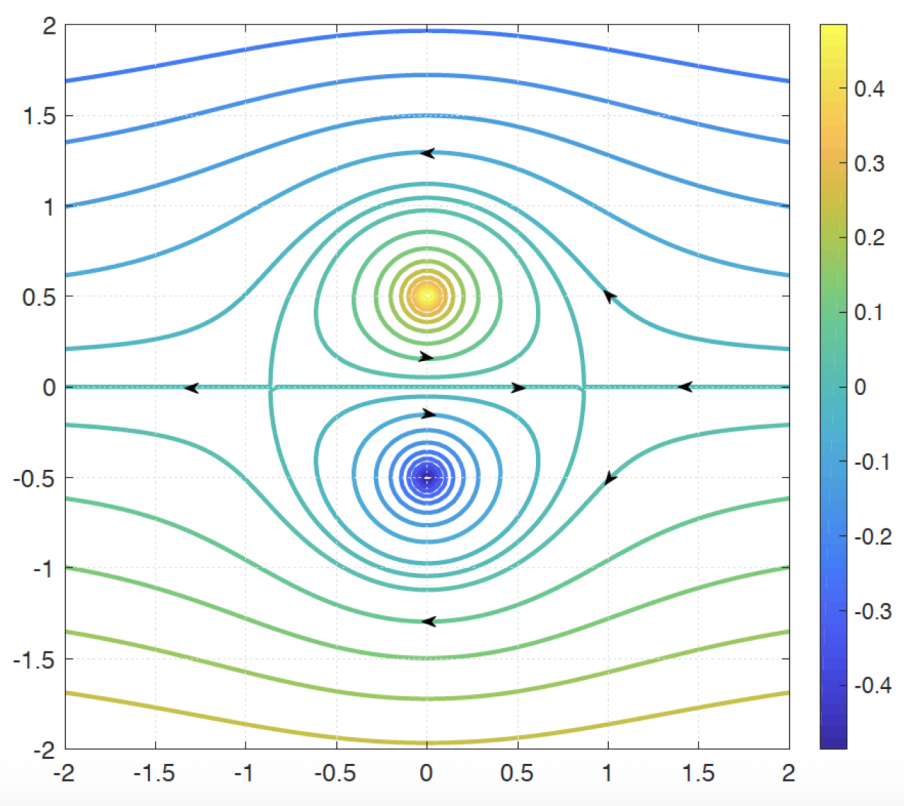
[3] Collinear interaction of vortex pairs with different strengths - criteria for leapfrogging Journal, PDF *Editor's Pick*
C. Mavroyiakoumou, F. Berkshire, Physics of Fluids, 32, 023603 (2020) We formulate a system of equations that describes the motion of four vortices made up of two interacting vortex pairs, where the absolute strengths of the pairs are different. Each vortex pair moves along the same axis in the same sense. In much of the literature, the vortex pairs have equal strength. The vortex pairs can either escape to infinite separation or undergo a periodic leapfrogging motion. We determine an explicit criterion in terms of the initial horizontal separation of the vortex pairs given as a function of the ratio of their strengths, to describe a periodic leapfrogging motion when interacting along the line of symmetry. In an appendix we also contrast a special case of interaction of a vortex pair with a single vortex of the same strength in which a vortex exchange occurs.
C. Mavroyiakoumou, F. Berkshire, Physics of Fluids, 32, 023603 (2020) We formulate a system of equations that describes the motion of four vortices made up of two interacting vortex pairs, where the absolute strengths of the pairs are different. Each vortex pair moves along the same axis in the same sense. In much of the literature, the vortex pairs have equal strength. The vortex pairs can either escape to infinite separation or undergo a periodic leapfrogging motion. We determine an explicit criterion in terms of the initial horizontal separation of the vortex pairs given as a function of the ratio of their strengths, to describe a periodic leapfrogging motion when interacting along the line of symmetry. In an appendix we also contrast a special case of interaction of a vortex pair with a single vortex of the same strength in which a vortex exchange occurs.
[2] Mathematical modelling of a viscida network Journal, PDF
C. Mavroyiakoumou, I. M. Griffiths, P. D. Howell, Journal of Fluid Mechanics, 872, 147-176 (2019)
We develop a general model to describe a network of interconnected thin viscous sheets, or viscidas, which evolve under the action of surface tension. A junction between two viscidas is analysed by considering a single viscida containing a smoothed corner, where the centreline angle changes rapidly, and then considering the limit as the smoothing tends to zero. The analysis is generalized to derive a simple model for the behaviour at a junction between an arbitrary number of viscidas, which is then coupled to the governing equation for each viscida. We thus obtain a general theory, consisting of N partial differential equations and 3J algebraic conservation laws, for a system of N viscidas connected at J junctions. This approach provides a framework to understand the fabrication of microstructured optical fibres containing closely spaced holes separated by interconnected thin viscous struts. We show sample solutions for simple networks with J=2 and N=2 or 3. We also demonstrate that there is no uniquely defined junction model to describe interconnections between viscidas of different thicknesses. Link to introductory video by I. M. Griffiths: https://www.youtube.com/watch?v=k4fmxj26n9w
C. Mavroyiakoumou, I. M. Griffiths, P. D. Howell, Journal of Fluid Mechanics, 872, 147-176 (2019)
We develop a general model to describe a network of interconnected thin viscous sheets, or viscidas, which evolve under the action of surface tension. A junction between two viscidas is analysed by considering a single viscida containing a smoothed corner, where the centreline angle changes rapidly, and then considering the limit as the smoothing tends to zero. The analysis is generalized to derive a simple model for the behaviour at a junction between an arbitrary number of viscidas, which is then coupled to the governing equation for each viscida. We thus obtain a general theory, consisting of N partial differential equations and 3J algebraic conservation laws, for a system of N viscidas connected at J junctions. This approach provides a framework to understand the fabrication of microstructured optical fibres containing closely spaced holes separated by interconnected thin viscous struts. We show sample solutions for simple networks with J=2 and N=2 or 3. We also demonstrate that there is no uniquely defined junction model to describe interconnections between viscidas of different thicknesses. Link to introductory video by I. M. Griffiths: https://www.youtube.com/watch?v=k4fmxj26n9w
[1] The QRD and SVD of matrices over a real algebra Journal, arXiv
P. Ginzberg, C. Mavroyiakoumou, Linear Algebra and its Applications, 504, 27-47 (2016)
Recent work in the field of signal processing has shown that the singular value decomposition of a matrix with entries in certain real algebras can be a powerful tool. In this article we show how to generalise the QR decomposition and SVD to a wide class of real algebras, including all finite-dimensional semi-simple algebras, (twisted) group algebras and Clifford algebras. Two approaches are described for computing the QRD/SVD: one Jacobi method with a generalised Givens rotation, and one based on the Artin–Wedderburn theorem.
P. Ginzberg, C. Mavroyiakoumou, Linear Algebra and its Applications, 504, 27-47 (2016)
Recent work in the field of signal processing has shown that the singular value decomposition of a matrix with entries in certain real algebras can be a powerful tool. In this article we show how to generalise the QR decomposition and SVD to a wide class of real algebras, including all finite-dimensional semi-simple algebras, (twisted) group algebras and Clifford algebras. Two approaches are described for computing the QRD/SVD: one Jacobi method with a generalised Givens rotation, and one based on the Artin–Wedderburn theorem.
Proceedings
[1] Optimizing the performance of a conical ceramic membrane Report, PDF
I. M. Griffiths et al., Proc. 146th European Study Group with Industry (2019)
I. M. Griffiths et al., Proc. 146th European Study Group with Industry (2019)
Theses
[2] Membrane Flutter in Inviscid Flow PDF
C. Mavroyiakoumou, PhD Thesis (July 2022)
Advisor: Prof. Silas Alben
C. Mavroyiakoumou, PhD Thesis (July 2022)
Advisor: Prof. Silas Alben
[1] Mathematical Modelling of Microstructured Optical Fibres
C. Mavroyiakoumou, MSc Thesis (Trinity Term and Summer 2017)
Advisors: Prof. Ian Griffiths and Prof. Peter Howell
C. Mavroyiakoumou, MSc Thesis (Trinity Term and Summer 2017)
Advisors: Prof. Ian Griffiths and Prof. Peter Howell
Other projects
[7] Solving Non-linear Elasticity BVPs in FEniCS: Bifurcations and Buckling of Beams PDF
C. Mavroyiakoumou, Prof. Patrick Farrell, Python in Scientific Computing (Trinity Term 2017)
C. Mavroyiakoumou, Prof. Patrick Farrell, Python in Scientific Computing (Trinity Term 2017)
[6] Stokes Flow and Free Boundaries PDF
C. Mavroyiakoumou, Prof. Peter Howell, Applied Complex Variables (Hilary Term 2017)
C. Mavroyiakoumou, Prof. Peter Howell, Applied Complex Variables (Hilary Term 2017)
[5] Modelling Soil Erosion and Bed Formation in Shallow Overland Flow PDF
C. Mavroyiakoumou, Prof. Graham Sander, Case Study for Mathematical Modelling (Hilary Term 2017)
C. Mavroyiakoumou, Prof. Graham Sander, Case Study for Mathematical Modelling (Hilary Term 2017)
[4] Numerical Linear Algebra: Comparison of Several Numerical Methods used to solve Poisson's Equation PDF
C. Mavroyiakoumou, Dr. Kathryn Gillow, Case Study for Scientific Computing (Hilary Term 2017)
C. Mavroyiakoumou, Dr. Kathryn Gillow, Case Study for Scientific Computing (Hilary Term 2017)
[3] Sliding Glaciers and Cavitation PDF
C. Mavroyiakoumou, Prof. Ian Hewitt, Mathematical Geoscience (Michaelmas Term 2016)
C. Mavroyiakoumou, Prof. Ian Hewitt, Mathematical Geoscience (Michaelmas Term 2016)
[2] Dynamics of Interacting Vortices - the restricted three vortex problem and leapfrogging of vortex pairs
C. Mavroyiakoumou, Dr. Frank Berkshire, UROP research project (Summer 2015)
C. Mavroyiakoumou, Dr. Frank Berkshire, UROP research project (Summer 2015)
[1] A Network of Mathematical Theorems PDF
C. Mavroyiakoumou, Dr. Nick Jones, Second year group project (June 2015)
C. Mavroyiakoumou, Dr. Nick Jones, Second year group project (June 2015)