| [1] |
Peherstorfer, B., Willcox, K. & Gunzburger, M. Survey of multifidelity methods in uncertainty propagation, inference, and optimization.
SIAM Review, 60(3):550-591, 2018. [Abstract]Abstract
In many situations across computational science and engineering, multiple computational models are available that describe a system of interest. These different models have varying evaluation costs and varying fidelities. Typically, a computationally expensive high-fidelity model describes the system with the accuracy required by the current application at hand, while lower-fidelity models are less accurate but computationally cheaper than the high-fidelity model. Outer-loop applications, such as optimization, inference, and uncertainty quantification, require multiple model evaluations at many different inputs, which often leads to computational demands that exceed available resources if only the high-fidelity model is used. This work surveys multifidelity methods that accelerate the solution of outer-loop applications by combining high-fidelity and low-fidelity model evaluations, where the low-fidelity evaluations arise from an explicit low-fidelity model (e.g., a simplified physics approximation, a reduced model, a data-fit surrogate, etc.) that approximates the same output quantity as the high-fidelity model. The overall premise of these multifidelity methods is that low-fidelity models are leveraged for speedup while the high-fidelity model is kept in the loop to establish accuracy and/or convergence guarantees. We categorize multifidelity methods according to three classes of strategies: adaptation, fusion, and filtering. The paper reviews multifidelity methods in the outer-loop contexts of uncertainty propagation, inference, and optimization. [BibTeX]@article{PWG17MultiSurvey,
title = {Survey of multifidelity methods in uncertainty propagation, inference, and optimization},
author = {Peherstorfer, B. and Willcox, K. and Gunzburger, M.},
journal = {SIAM Review},
volume = {60},
number = {3},
pages = {550-591},
year = {2018},
} |
| [2] |
Maurais, A., Alsup, T., Peherstorfer, B. & Marzouk, Y. Multi-fidelity covariance estimation in the log-Euclidean geometry.
International Conference on Machine Learning (ICML), 2023. [Abstract]Abstract
We introduce a multi-fidelity estimator of covariance matrices that employs the log-Euclidean geometry of the symmetric positive-definite manifold. The estimator fuses samples from a hierarchy of data sources of differing fidelities and costs for variance reduction while guaranteeing definiteness, in contrast with previous approaches. The new estimator makes covariance estimation tractable in applications where simulation or data collection is expensive; to that end, we develop an optimal sample allocation scheme that minimizes the mean-squared error of the estimator given a fixed budget. Guaranteed definiteness is crucial to metric learning, data assimilation, and other downstream tasks. Evaluations of our approach using data from physical applications (heat conduction, fluid dynamics) demonstrate more accurate metric learning and speedups of more than one order of magnitude compared to benchmarks. [BibTeX]@inproceedings{MAPY23LEMF,
title = {Multi-fidelity covariance estimation in the log-Euclidean geometry},
author = {Maurais, A. and Alsup, T. and Peherstorfer, B. and Marzouk, Y.},
journal = {International Conference on Machine Learning (ICML)},
year = {2023},
} |
| [3] |
Peherstorfer, B. Multifidelity Monte Carlo estimation with adaptive low-fidelity models.
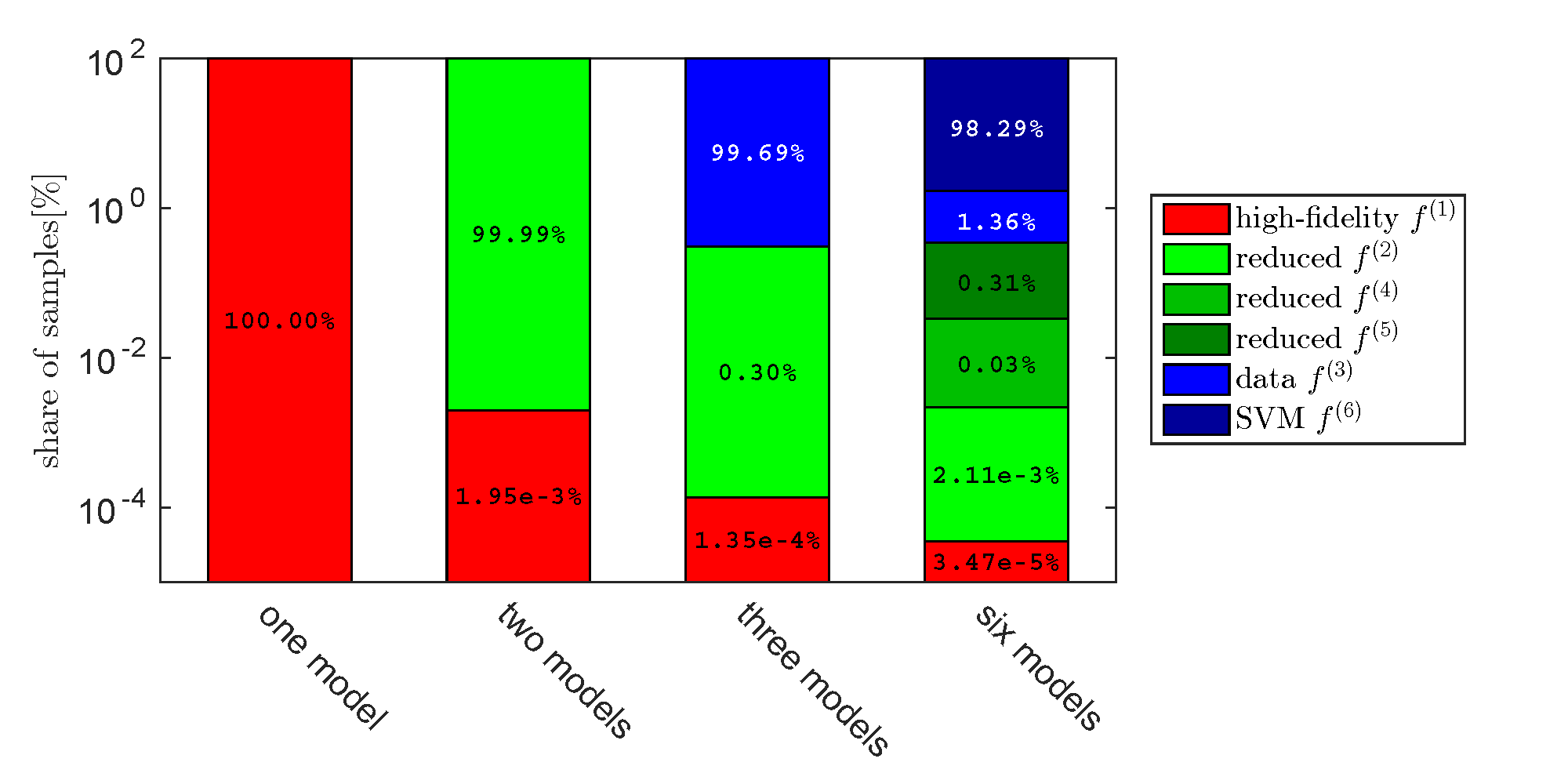
SIAM/ASA Journal on Uncertainty Quantification, 7:579-603, 2019. [Abstract]Abstract
Multifidelity Monte Carlo (MFMC) estimation combines low- and high-fidelity models to speedup the estimation of statistics of the high-fidelity model outputs. MFMC optimally samples the low- and high-fidelity models such that the MFMC estimator has minimal mean-squared error for a given computational budget. In the setup of MFMC, the low-fidelity models are static, i.e., they are given and fixed and cannot be changed and adapted. We introduce the adaptive MFMC (AMFMC) method that splits the computational budget between adapting the low-fidelity models to improve their approximation quality and sampling the low- and high-fidelity models to reduce the mean-squared error of the estimator. Our AMFMC approach derives the quasi-optimal balance between adaptation and sampling in the sense that our approach minimizes an upper bound of the mean-squared error, instead of the error directly. We show that the quasi-optimal number of adaptations of the low-fidelity models is bounded even in the limit case that an infinite budget is available. This shows that adapting low-fidelity models in MFMC beyond a certain approximation accuracy is unnecessary and can even be wasteful. Our AMFMC approach trades-off adaptation and sampling and so avoids over-adaptation of the low-fidelity models. Besides the costs of adapting low-fidelity models, our AMFMC approach can also take into account the costs of the initial construction of the low-fidelity models (``offline costs''), which is critical if low-fidelity models are computationally expensive to build such as reduced models and data-fit surrogate models. Numerical results demonstrate that our adaptive approach can achieve orders of magnitude speedups compared to MFMC estimators with static low-fidelity models and compared to Monte Carlo estimators that use the high-fidelity model alone. [BibTeX]@article{P19AMFMC,
title = {Multifidelity Monte Carlo estimation with adaptive low-fidelity models},
author = {Peherstorfer, B.},
journal = {SIAM/ASA Journal on Uncertainty Quantification},
volume = {7},
pages = {579-603},
year = {2019},
} |