[1]   N. Alon, A. Andoni, T. Kaufman, K. Matulef, R. Rubinfeld, and N. Xie: Testing k-wise and almost k-wise independence. In Proc. 39th STOC, pp. 496–505. ACM Press, 2007. [STOC:1250790.1250863].

[2]   A. Ambainis: A note on quantum black-box complexity of almost all Boolean functions. Inform. Process. Lett., 71(1):5–7, 1999. [IPL:10.1016/S0020-0190(99)00079-4].

[3]   S. Arora and B. Barak: Complexity Theory: A Modern Approach. Cambridge University Press, 2009. To appear. Preliminary version available at http://www.cs.princeton.edu/theory/complexity.

[4]   S. Arora, C. Lund, R. Motwani, M. Sudan, and M. Szegedy: Proof verification and the hardness of approximation problems. J. ACM, 45(3):501–555, 1998. Earlier version in FOCS’92. [JACM:278298.278306].

[5]   K. Arrow: A difficulty in the concept of social welfare. J. Political Economy, 58(4):328–346, 1950. [doi:10.1086/256963].

[6]   W. Beckner: Inequalities in Fourier analysis. Ann. of Math., 102:159–182, 1975.

[7]   A. Ben-Aroya, O. Regev, and R. de Wolf: A hypercontractive inequality for matrix-valued functions with applications to quantum computing. In Proc. 49th FOCS. IEEE Computer Society Press, 2008.

[8]   M. Ben-Or and N. Linial: Collective coin flipping. In S. Micali, editor, Randomness and Computation, pp. 91–115. JAI Press, 1989. Earlier version in FOCS’85.

[9]   A. Bernasconi, B. Codenotti, and J. Simon: On the Fourier analysis of Boolean functions. Technical Report IMC B4-97-03, Istituto di Matematica Computazionale, Pisa, 1997.

[10]   A. Bonami: Étude des coefficients de Fourier des fonctions de L^p(G). Annales de l’Institut Fourier, 20(2):335–402, 1970.

[11]   J. Bourgain: On the distribution of the Fourier spectrum of Boolean functions. Israel J. Math., 131(1):269–276, 2002. [Springer:657221r06x818652].

[12]   J. Bourgain, J. Kahn, G. Kalai, G. Katznelson, and N. Linial: The influence of variables in product spaces. Israel J. Math., 77(1–2):55–64, 1992. [Springer:456880489w184683].

[13]   N. Bshouty, E. Mossel, R. O’Donnell, and R. Servedio: Learning DNF from random walks. J. Comput. System Sci., 71(3):250–265, 2005. Earlier version in FOCS’03. [JCSS:10.1016/j.jcss.2004.10.010].

[14]   H. Buhrman, N. Vereshchagin, and R. de Wolf: On computation and communication with small bias. In Proc. 22nd Conference on Comput. Complexity, pp. 24–32. IEEE Computer Society Press, 2007. [CCC:10.1109/CCC.2007.18].

[15]   H. Buhrman and R. de Wolf: Complexity measures and decision tree complexity: A survey. Theoret. Comput. Sci., 288(1):21–43, 2002. [TCS:10.1016/S0304-3975(01)00144-X].

[16]   S. Chawla, R. Krauthgamer, R. Kumar, Y. Rabani, and D. Sivakumar: On the hardness of approximating sparsest cut and multicut. In Proc. 20th Conf. Comput. Complexity, pp. 144–153. IEEE Computer Society Press, 2005. [CCC:10.1109/CCC.2005.20].

[17]   I. Dinur: The PCP theorem by gap amplification. J. ACM, 54(3):12, 2007. Earlier version in STOC’06. [JACM:10.1145/1236457.1236459].

[18]   I. Dinur, E. Friedgut, G. Kindler, and R. O’Donnell: On the Fourier tails of bounded functions over the discrete cube. Israel J. Math., 160(1):389–412, 2007. Earlier version in STOC’06. [Springer:43k0r5p3g28k508g, STOC:10.1145/1132516.1132580].

[19]   I. Dinur, E. Mossel, and O. Regev: Conditional hardness for approximate coloring. In Proc. 38nd STOC, pp. 344–353. ACM Press, 2006. [STOC:1132516.1132567].

[20]   P. Erd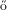s and A. Rényi: On random graphs I. Publicationes Mathematicae, 6:290–297, 1959.

[21]   E. Fischer, G. Kindler, D. Ron, S. Safra, and A. Samorodnitsky: Testing juntas. J. Comput. System Sci., 68(4):753–787, 2004. Earlier version in FOCS’02. [JCSS:10.1016/j.jcss.2003.11.004].

[22]   E. Friedgut: Boolean functions with low average sensitivity depend on few coordinates. Combinatorica, 18(1):27–35, 1998. [Springer:fxcj48rnbwv5gjdb].

[23]   E. Friedgut: Influences in product spaces: KKL and BKKKL revisited. Combin. Probab. Comput., 13(1):17–29, 2004. [Cambridge:10.1017/S0963548303005832].

[24]   E. Friedgut and G. Kalai: Every monotone graph property has a sharp threshold. Proc. Amer. Math. Soc., 124:2993–3002, 1996.

[25]   E. Friedgut, G. Kalai, and A. Naor: Boolean functions whose Fourier transform is concentrated at the first two levels. Adv. in Appl. Math., 29(3):427–437, 2002. [Elsevier:10.1016/S0196-8858(02)00024-6].

[26]   E. Friedgut, G. Kalai, and N. Nisan: Elections can be manipulated often. In Proc. 49th FOCS. IEEE Computer Society Press, 2008.

[27]   D. Gavinsky, J. Kempe, I. Kerenidis, R. Raz, and R. de Wolf: Exponential separations for one-way quantum communication complexity, with applications to cryptography. In Proc. 39th STOC, pp. 516–525. ACM Press, 2007. [STOC:1250790.1250866].

[28]   O. Goldreich and L. Levin: A hard-core predicate for all one-way functions. In Proc. 21st STOC, pp. 25–32. ACM Press, 1989. [STOC:73007.73010].

[29]   L. Gross: Logarithmic Sobolev inequalities. Amer. J. Math., 97(4):1061–1083, 1975.

[30]   V. Guruswami: Algorithmic Results in List Decoding, volume 2(2) of Foundations and Trends in Theoretical Computer Science. Now Publishers, 2007.

[31]   J. Håstad: Some optimal inapproximability results. J. ACM, 48(4):798–859, 2001. Earlier version in STOC’97. [JACM:10.1145/502090.502098].

[32]   J. Jackson: An efficient membership-query algorithm for learning DNF with respect to the uniform distribution. J. Comput. System Sci., 55(3):414–440, 1997. Earlier version in FOCS’94. [JCSS:10.1006/jcss.1997.1533].

[33]   S. Janson: Gaussian Hilbert Spaces, volume 129 of Cambridge Tracts in Mathematics. Cambridge University Press, 1997.

[34]   J. Kahn, G. Kalai, and N. Linial: The influence of variables on Boolean functions. In Proc. 29th FOCS, pp. 68–80. IEEE Computer Society Press, 1988.

[35]   G. Kalai: Noise sensitivity and chaos in social choice theory. Technical report, Discussion Paper Series dp399. Center for rationality and interactive decision theory, Hebrew University, 2005. Available at http://www.ma.huji.ac.il/~kalai/CHAOS.pdf.

[36]   G. Kalai and S. Safra: Threshold phenomena and influence. In Percus et al. [58], pp. 25–60.

[37]   S. Khot: On the power of unique 2-prover 1-round games. In Proc. 34th STOC, pp. 767–775. ACM Press, 2002. [STOC:509907.510017].

[38]   S. Khot, G. Kindler, E. Mossel, and R. O’Donnell: Optimal inapproximability results for MAX-CUT and other 2-variable CSPs? SIAM J. Comput., 37(1):319–357, 2007. [SICOMP:10.1137/S0097539705447372].

[39]   S. Khot and R. O’Donnell: SDP gaps and UGC-hardness for MAXCUTGAIN. In Proc. 47th FOCS, pp. 217–226. IEEE Computer Society Press, 2006. [FOCS:10.1109/FOCS.2006.67].

[40]   S. Khot and O. Regev: Vertex cover might be hard to approximate to within 2 -ε. J. Comput. System Sci., 74(3):335–349, 2008. Earlier version in Complexity’03. [JCSS:10.1016/j.jcss.2007.06.019].

[41]   S. Khot and N. Vishnoi: The unique games conjecture, integrality gap for cut problems and embeddability of negative type metrics into ℓ₁. In Proc. 46th FOCS, pp. 53–62. IEEE Computer Society Press, 2005. [FOCS:10.1109/SFCS.2005.74].

[42]   H. Klauck: Lower bounds for quantum communication complexity. SIAM J. Comput., 37(1):20–46, 2007. Earlier version in FOCS’01. [SICOMP:10.1137/S0097539702405620].

[43]   A. Klivans and R. Servedio: Learning DNF in time 2^Õ(n1∕3) . J. Comput. System Sci., 68(2):303–318, 2004. Earlier version in STOC’01. [JCSS:10.1016/j.jcss.2003.07.007].

[44]   E. Kushilevitz and Y. Mansour: Learning decision trees using the Fourier spectrum. SIAM J. Comput., 22(6):1331–1348, 1993. Earlier version in STOC’91. [SICOMP:10.1137/0222080].

[45]   J. R. Lee and A. Naor: Embedding the diamond graph in L_p and dimension reduction in L₁. Geom. Funct. Anal., 14(4):745–747, 2004. [Springer:r36q4553fwheur9u].

[46]   N. Linial, Y. Mansour, and N. Nisan: Constant depth circuits, Fourier transform, and learnability. J. ACM, 40(3):607–620, 1993. Earlier version in FOCS’89. [JACM:10.1145/502090.502098].

[47]   F. MacWilliams and N. Sloane: The Theory of Error-Correcting Codes. North-Holland, 1977.

[48]   Y. Mansour: An O(n^{log log n}) learning algorithm for DNF under the uniform distribution. J. Comput. System Sci., 50(3):543–550, 1995. Earlier version in COLT’92. [JCSS:10.1006/jcss.1995.1043].

[49]   E. Mossel, R. O’Donnell, and K. Oleszkiewicz: Noise stability of functions with low influences: invariance and optimality. Ann. of Math., 2008. To appear. Earlier version in FOCS’05.

[50]   E. Mossel, R. O’Donnell, and R. Servedio: Learning functions of k relevant variables. J. Comput. System Sci., 69(3):421–434, 2004. Earlier version in STOC’03. [JCSS:10.1016/j.jcss.2004.04.002].

[51]   M. Navon and A. Samorodnitsky: On Delsarte’s linear programming bounds for binary codes. In Proc. 46th FOCS, pp. 327–338. IEEE Computer Society Press, 2005. [FOCS:10.1109/SFCS.2005.55].

[52]   N. Nisan and M. Szegedy: On the degree of Boolean functions as real polynomials. Comput. Complexity, 4(4):301–313, 1994. Earlier version in STOC’92. [CC:p1711275700w5264].

[53]   R. O’Donnell: Lecture notes for a course “Analysis of Boolean functions”, 2007. Available at http://www.cs.cmu.edu/~odonnell/boolean-analysis.

[54]   R. O’Donnell: Some topics in analysis of Boolean functions. Technical report, ECCC Report TR08–055, 2008. Paper for an invited talk at STOC’08. [ECCC:TR08-055].

[55]   R. O’Donnell, M. Saks, O. Schramm, and R. Servedio: Every decision tree has an influential variable. In Proc. 46th FOCS, pp. 31–39. IEEE Computer Society Press, 2005. [FOCS:10.1109/SFCS.2005.34].

[56]   R. O’Donnell and R. Servedio: Extremal properties of polynomial threshold functions. In Proc. 18th Conf. Comput. Complexity, pp. 3–12. IEEE Computer Society Press, 2003.

[57]   R. O’Donnell and R. Servedio: Learning monotone decision trees in polynomial time. SIAM J. Comput., 37(3):827–844, 2007. Earlier version in Complexity’06. [SICOMP:10.1137/060669309].

[58]   A.G. Percus, G. Istrate, and C. Moore, editors. Computational Complexity and Statistical Physics. Oxford University Press, 2006.

[59]   P. Raghavendra: Optimal algorithms and inapproximability results for every CSP? In Proc. 40th STOC, pp. 245–254. ACM Press, 2008. [STOC:1374376.1374414].

[60]   R. Raz: Fourier analysis for probabilistic communication complexity. Comput. Complexity, 5(3/4):205–221, 1995. [CC:p7346675080r85r4].

[61]   J. T. Schwartz: Fast probabilistic algorithms for verification of polynomial identities. J. ACM, 27(4):701–717, 1980. [JACM:10.1145/322217.322225].

[62]   R. Servedio: Every linear threshold function has a low-weight approximator. Comput. Complexity, 16(2):180–209, 2007. Earlier version in Complexity’06. [CC:64682257x6344776].

[63]   A. Sherstov: Communication lower bounds using dual polynomials. Technical report, ECCC Report TR08–057, 2008. [ECCC:TR08-057].

[64]   Y. Shi: Lower bounds of quantum black-box complexity and degree of approximating polynomials by influence of Boolean variables. Inform. Process. Lett., 75(1–2):79–83, 2000. [IPL:10.1016/S0020-0190(00)00069-7].

[65]    D. Štefankovič: Fourier transforms in computer science. Master’s thesis, University of Chicago, Department of Computer Science, 2000. Available at http://www.cs.rochester.edu/~stefanko/Publications/Fourier.ps.

[66]   M. Sudan: List decoding: Algorithms and applications. In Proc. Intern. Conf. IFIP TCS, volume 1872 of Lect. Notes in Comput. Sci., pp. 25–41. Springer, 2000.

[67]   M. Talagrand: On Russo’s approximate 0-1 law. Ann. Probab., 22(3):1576–1587, 1994. http://projecteuclid.org/euclid.aop/1176988612.

[68]   M. Talagrand: How much are increasing sets positively correlated? Combinatorica, 16(2):243–258, 1996. [Springer:uvm737238p44xk37].

[69]   R. E. Zippel: Probabilistic algorithms for sparse polynomials. In Proc. EUROSAM 79, volume 72 of Lect. Notes in Comput. Sci., pp. 216–226. Springer, 1979.