Research
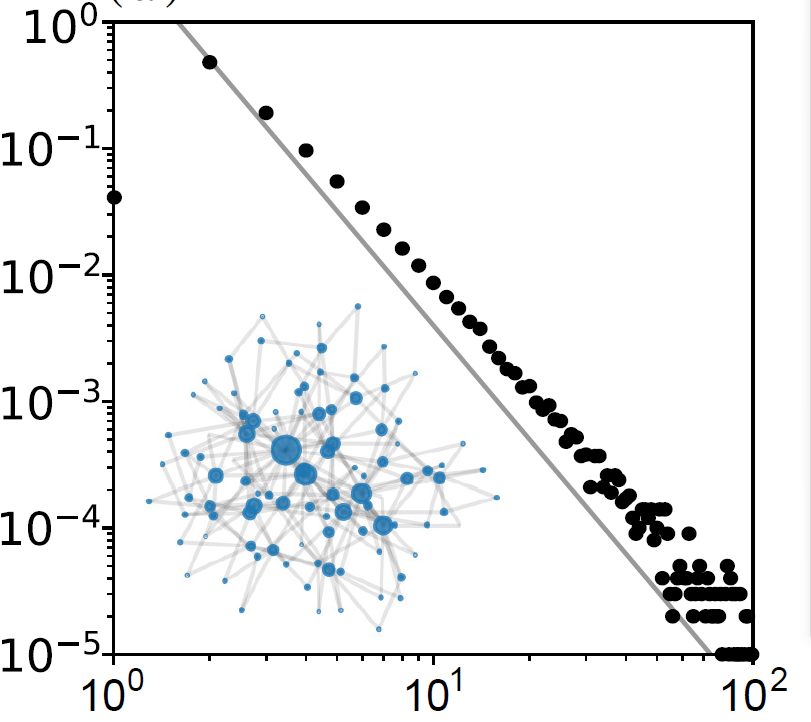
The details of a Barabasi-Albert network and the mean-field degree distribution of this network.
Modeling for multiscale problem
Multiscale problems in population dynamics as well as in other disciplines require mathematical modeling to link individuals' behavior with macroscopic quantities. Specifically, I am interested in applying kinetic theories to build rigorous mathematical models for describing such multiscale phenomena and learn how individuals' behavior would influence the mean-field level dynamics.
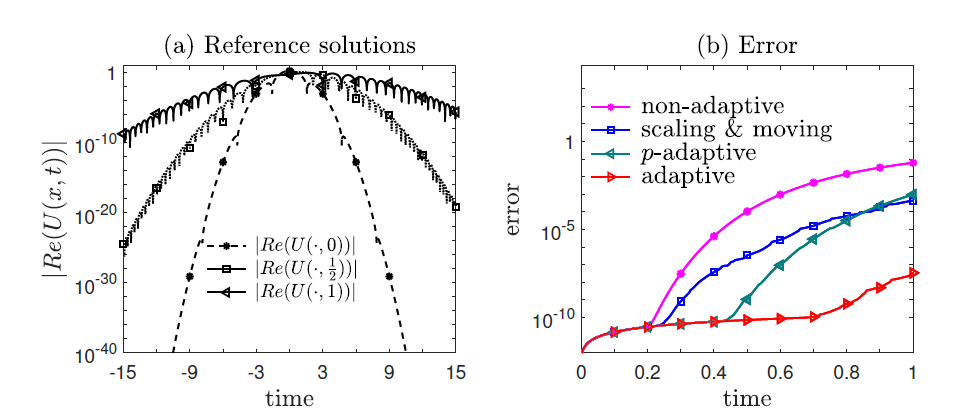
Applying the adaptive spectral method for solving a Schrödinger equation in the unbounded domain: very high accuracy could be achieved compared to non-adaptive spectral methods.
Spectral methods
Equations that describe multiscale models are sometimes defined in unbounded domains. Therefore, I am especially interested in applying spectral methods for unbounded domain PDEs. I developed a novel adaptive spectral method, and machine-learning-based spectral methods for solving both forward- and inverse-type PDE problems are of my current interest.

Applying the reinforcement-learning-based or Pontryagin-Maximum-Principle-based control algorithms to determine the allocation of limited test kits.
Control algorithms
I am interested in developing control algorithms for equations that describe the dynamics of multiscale systems, especially in biology and medicine. Particularly, I am interested in applying reinforcement learning in developing control algorithms. Reinforcement learning techniques could be combined with traditional control approaches to develop efficient algorithms for certain biological models.
Publication
Mingtao Xia, Xiangting Li, Qijing Shen Tom Chou, A Spectral Approach for Learning Spatiotemporal Neural Differential Equations, arXiv preprint: 2309.16131, (2023)
Tom Chou, Sihong Shao, Mingtao Xia, Adaptive Hermite Spectral Methods in Unbounded Domains, Applied Numerical Mathematics, 183, 201-220, (2023)