


Next: Solution in Mathematica
Up: No Title
Previous: No Title
Subsections
In this worksheet we continue exploring electromagnetism using
Mathematica and Fortran. We will now study the motion of charged particles
in crossed electric and magnetic fields. This will necessitate solving
ordinary differential equations (ODE's). This will be our last worksheet for
this semester. We hope you enjoyed learning more about Mathematica
and being introduced to Fortran. We have by no means covered either one
exhaustively, and hopefully you will continue learning more about
computational physics throughout your education and career.
You will have three class periods for this worksheet.
Consider the motion of a particle with charge q with initial velocity
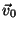 in an electromagnetic field with electric field
in an electromagnetic field with electric field
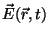 and magnetic field
and magnetic field
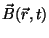 .
In general, these can be any
function of coordinates and time, but in this worksheet we will restrict our
attention to the case when the direction of the fields is fixed, and their
magnitudes oscillate harmonically with a frequency
.
In general, these can be any
function of coordinates and time, but in this worksheet we will restrict our
attention to the case when the direction of the fields is fixed, and their
magnitudes oscillate harmonically with a frequency 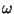 and amplitudes
and amplitudes
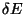 and
and 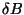 around E0 and B0. If we let the angle
between
around E0 and B0. If we let the angle
between 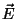 and
and 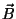 be
be 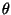 and the phase displacement
between their oscillation
and the phase displacement
between their oscillation 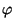 ,
then it is quite general to assume
that:
,
then it is quite general to assume
that:
In the worksheet we will consider only specific simpler cases of this
general case.
The classical motion of the particle in such a field is determined by
Newton's equation of motion, where the force is given by:
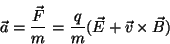 |
(2) |
As usual, we will be interested mostly in qualitative understanding of the
motion, so set
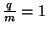 .
We can now write this as an ODE for
.
We can now write this as an ODE for
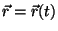 with a given initial velocity
with a given initial velocity
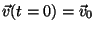 and
starting position
and
starting position
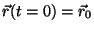 :
:
More formally, equation ![[*]](/misc/icons.gif/cross_ref_motif.gif) is what is known as a second
order initial value problem (IVP), and there are many numerical techniques
aimed at solving this type of extremely common equation. Mathematica
's function NDSolve is equipped with a suite of such techniques,
and there many Fortran libraries that solve problems of the type
is what is known as a second
order initial value problem (IVP), and there are many numerical techniques
aimed at solving this type of extremely common equation. Mathematica
's function NDSolve is equipped with a suite of such techniques,
and there many Fortran libraries that solve problems of the type ![[*]](/misc/icons.gif/cross_ref_motif.gif) as well.
When approaching a problem numerically, it is usually wise to write in the
most general (yet specific) way, so that the same numerical algorithm can be
used for a variety of problems. A typical second order IVP has the form:
as well.
When approaching a problem numerically, it is usually wise to write in the
most general (yet specific) way, so that the same numerical algorithm can be
used for a variety of problems. A typical second order IVP has the form:
Look at equation ![[*]](/misc/icons.gif/cross_ref_motif.gif) and identify all the variables in the above
equation before proceeding.
Most numerical methods are tailored for the first order IVP,
and identify all the variables in the above
equation before proceeding.
Most numerical methods are tailored for the first order IVP,
since any problem of order n, such as ![[*]](/misc/icons.gif/cross_ref_motif.gif) (n=2), can be cast as
a first order problem by introducing auxiliary variables for the n-1 lower
derivatives. For example, eq.
(n=2), can be cast as
a first order problem by introducing auxiliary variables for the n-1 lower
derivatives. For example, eq. ![[*]](/misc/icons.gif/cross_ref_motif.gif) can be written in the form of eq.
can be written in the form of eq.
![[*]](/misc/icons.gif/cross_ref_motif.gif) by introducing a new variable for the first derivative
by introducing a new variable for the first derivative
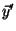 (velocity):
(velocity):
Although this is formally system of first order IVP's, it is in fact
equivalent to a formal first order IVP for the variable that appends the
first derivative with the variable itself,
![$\vec{Y}=[\vec{y}^{\prime }\vdots
\vec{y}]$](img35.gif) ,
,
so that any method that can solve ![[*]](/misc/icons.gif/cross_ref_motif.gif) can also solve
can also solve ![[*]](/misc/icons.gif/cross_ref_motif.gif) and thus also
and thus also ![[*]](/misc/icons.gif/cross_ref_motif.gif) . Before proceeding, rewrite equation
. Before proceeding, rewrite equation ![[*]](/misc/icons.gif/cross_ref_motif.gif) as
a first order IVP (either in the form
as
a first order IVP (either in the form ![[*]](/misc/icons.gif/cross_ref_motif.gif) or
or ![[*]](/misc/icons.gif/cross_ref_motif.gif) )
and show your result to your teacher or TA.
From here on we will only discuss problem
)
and show your result to your teacher or TA.
From here on we will only discuss problem ![[*]](/misc/icons.gif/cross_ref_motif.gif) , having in mind the
previous discussion. The simplest numerical method for solving such an
equation is Euler's method, which steps through the independent variable
(time) in small time steps dx from the current value x, using a
first-order Taylor expansion to approximate the dependent variable y at
the next time step x+dx:
, having in mind the
previous discussion. The simplest numerical method for solving such an
equation is Euler's method, which steps through the independent variable
(time) in small time steps dx from the current value x, using a
first-order Taylor expansion to approximate the dependent variable y at
the next time step x+dx:
It is clear that once we have an equation for 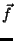 we can start from
the initial point x0 and step through time until any desired point to
obtain an approximate solution for the IVP. Euler method is very slow and a
very small step size dx is needed to achieve good results, but it is
prototypical of the commonly used methods, such as Runge-Kutta methods (see
Numerical Recipies for a description, or the file
/classes/phy201/RK4.f90).
we can start from
the initial point x0 and step through time until any desired point to
obtain an approximate solution for the IVP. Euler method is very slow and a
very small step size dx is needed to achieve good results, but it is
prototypical of the commonly used methods, such as Runge-Kutta methods (see
Numerical Recipies for a description, or the file
/classes/phy201/RK4.f90).



Next: Solution in Mathematica
Up: No Title
Previous: No Title
Aleksandar Donev
2000-12-12
![$\vec{Y}=[\vec{y}^{\prime }\vdots
\vec{y}]$](img35.gif) ,
,