


Next: About this document ...
Up: No Title
Previous: No Title
Subsections
In this worksheet you will use Mathematica and Fortran to calculate
the magnetostatic field of a current-carrying ring by numerically
integrating the Bio-Savart law. You will need to do the bulk of the
calculation in both Mathematica and Fortran, and you will have two
weeks to complete this worksheet. There will be no new Fortran material in
this worksheet, and as usual Mathematica's on-line help will be
enough. Make sure you review basic magnetostatics, in particular
Bio-Savart's law for the magnetic field of a current-carrying wire.
Consider current I flowing in a circular ring of radius R=1 unit. Also
assume that
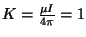 in these units. Choose the ring so
that it is centered at (0,0,0), and that it lies in the xy plane. Use
the Biot-Savart law to find the magnetic field due to this current ring at
an arbitrary point (x,0,z) in the xz plane (i.e. a plane perpendicular
to the plane of the ring). Note that this gives the field at any point since
there is cylindrical symmetry about the z axis.
A few reminders:
The contribution from a small directed element of length
in these units. Choose the ring so
that it is centered at (0,0,0), and that it lies in the xy plane. Use
the Biot-Savart law to find the magnetic field due to this current ring at
an arbitrary point (x,0,z) in the xz plane (i.e. a plane perpendicular
to the plane of the ring). Note that this gives the field at any point since
there is cylindrical symmetry about the z axis.
A few reminders:
The contribution from a small directed element of length 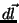 of a
wire carrying a current I to the magnetic field at a point
of a
wire carrying a current I to the magnetic field at a point 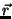 is
given by Bio-Savart's law:
is
given by Bio-Savart's law:
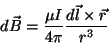 |
(1) |
Thus, to find the total magnetic field at a given point
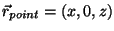 caused by a current-carrying ring, one needs to integrate
the expression in equation
caused by a current-carrying ring, one needs to integrate
the expression in equation ![[*]](/misc/icons.gif/cross_ref_motif.gif) (separately for each component, of
course) over elements of the ring at position
(separately for each component, of
course) over elements of the ring at position
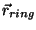 ,
,
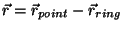 (draw a figure to help you understand this).
For a unit-radius ring in the xy plane, we can take the integration to be
over the polar angle
(draw a figure to help you understand this).
For a unit-radius ring in the xy plane, we can take the integration to be
over the polar angle 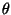 ,
so that
,
so that
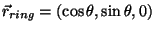 .
Also, for such a ring,
.
Also, for such a ring,
 ,
where
,
where 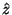 is the unit vector
in the z direction (i.e. perpendicular to the plane of the ring).
Now you have all the expressions you need to write down (in a few lines
using Mathematica--read next section if you wish) an expression
giving
is the unit vector
in the z direction (i.e. perpendicular to the plane of the ring).
Now you have all the expressions you need to write down (in a few lines
using Mathematica--read next section if you wish) an expression
giving  from the element of wire at a polar angle
from the element of wire at a polar angle 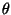 .
This
should have the form
.
This
should have the form
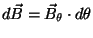 .
Show
your expression for
.
Show
your expression for
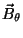 to your professor or TA
before working on the rest of this worksheet. Then, the total magnetic
field at the point
to your professor or TA
before working on the rest of this worksheet. Then, the total magnetic
field at the point
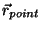 is simply the integral:
is simply the integral:
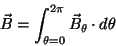 |
(2) |
Using the above expressions and the cross-product function Cross
find the expression for
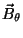 as a function of x, z and
as a function of x, z and 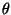 .
Then, using the function Integrate, integrate this
expression component-by-component over
.
Then, using the function Integrate, integrate this
expression component-by-component over
![$\theta =\left[ 0,2\pi \right] $](img18.gif) to
obtain the expression for
to
obtain the expression for 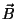 .
These integrals are so called elliptic
integrals and Mathematica can evaluate them. Choose a sample point,
for example x=0.3 and z=0.6, and evaluate the magnetic field at that
point.
In many cases an exact integral can not be found and one would then use
numerical integration (NIntegrate). Try this and see if you get the
same result as above. Which result had higher precision? Which do you think
was evaluated faster?
Now you can also plot the magnetic field of this ring in the xz plane as a
vector field. This should be a single line in Mathematica.
It was purely fortunate (due to the relatively simple geometry) that the
integrals above could be evaluated analytically. In most cases this has do
be done numerically. Fortran libraries by far surpass Mathematica in
speed when it comes to such numerical manipulations, but they are not nearly
as easy to use.
Before we attack the integration problem in eq.
.
These integrals are so called elliptic
integrals and Mathematica can evaluate them. Choose a sample point,
for example x=0.3 and z=0.6, and evaluate the magnetic field at that
point.
In many cases an exact integral can not be found and one would then use
numerical integration (NIntegrate). Try this and see if you get the
same result as above. Which result had higher precision? Which do you think
was evaluated faster?
Now you can also plot the magnetic field of this ring in the xz plane as a
vector field. This should be a single line in Mathematica.
It was purely fortunate (due to the relatively simple geometry) that the
integrals above could be evaluated analytically. In most cases this has do
be done numerically. Fortran libraries by far surpass Mathematica in
speed when it comes to such numerical manipulations, but they are not nearly
as easy to use.
Before we attack the integration problem in eq. ![[*]](/misc/icons.gif/cross_ref_motif.gif) , we need to
generalize it to a standard problem that can be applied to a variety of
problems and that is well studied in numerical analysis,
, we need to
generalize it to a standard problem that can be applied to a variety of
problems and that is well studied in numerical analysis,
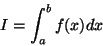 |
(3) |
where f(x) is more-or-less a well behaved function of x in [a,b].
There are many so-called quadrature formulae for numerically
calculating I, such as Newton-Cotes, Gauss and Romberg quadrature. A nice
desktop reference for these and many other numerical algorithms is
``Numerical Recipies in FORTRAN 77 and Fortran 90'', found at, for example,
http://lib-www.lanl.gov/numerical/.
The simplest, yet robust, quadrature is the trapezoid-rule
integration. It starts by splitting the interval [a,b] into N intervals
of equal length
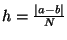 with positions
xi=a+ih
, 0<i<N. Then it is true that,
with positions
xi=a+ih
, 0<i<N. Then it is true that,
![\begin{displaymath}\int_{a}^{b}f(x)dx\approx h\sum_{i=1}^{N-1}f(x_{i})+\frac{h}{2}[f(a)+f(b)%
]+O(h^{2})
\end{displaymath}](img22.gif) |
(4) |
where O(h2) denotes error of order h2. It is easy to see that it
is not at all difficult to code ![[*]](/misc/icons.gif/cross_ref_motif.gif) in Fortran. Write a
function, say Trapezoid, that integrates a given function f(x) on
[a,b]. We've had examples of passing procedures as arguments to procedures
in the graphics routines, and although this is not in the manual, it's not
hard to understand. All one needs to do is provide an interface for
the procedure:
in Fortran. Write a
function, say Trapezoid, that integrates a given function f(x) on
[a,b]. We've had examples of passing procedures as arguments to procedures
in the graphics routines, and although this is not in the manual, it's not
hard to understand. All one needs to do is provide an interface for
the procedure:
FUNCTION Trapezoid(f,a,b,N) RESULT(I)
INTERFACE
FUNCTION f(x) RESULT(f_x) ! Function to be integrated
REAL, INTENT(IN) :: x
REAL :: f_x
END FUNCTION f
END INTERFACE
REAL, INTENT(IN) :: a,b ! The bounds
INTEGER, INTENT(IN) :: N
...
...Calculate I here using trapezoid rule using f and a DO loop...
...
END FUNCTION Trapezoid
Test this procedure on some simple example you already know the analytical
answer for. Next we describe a ready-made quadrature library. You don't have
to use it, but it isn't much different from using Trapezoid.
As usual, we made a simple wrapper routine for numerical integration,
AdaptiveIntegral, which in turn calls a ready-made adaptive
quadrature Fortran library taken from Adam Miller's Fortran 90 website. The
function is in the module Numerical_Integration, which is in our
class directory and you must USE in your program. This function
accepts a user function f to be integrated in a given finite range
[a,b] and returns the integral to within the desired relative or
absolute precisions relative_error and absolute_error
(these are both optional, so you don't need to specify them). An
estimate of the error in the result is returned in the argument
error_estimate, and the function also returns an error signal if the
integration failed (this is placed in the module variable error_flag
and you need not worry about it)
The interface to this function and the module variables are given here:
module Numerical_Integration
use Precision, only: wp ! wp=dp in the module Precision
use Adapt_Quad ! Read-made library
private
public :: AdaptiveIntegral ! The main routine
integer, save, public :: error_flag=0 ! An error flag (0 is success)
contains
function AdaptiveIntegral(f,a,b,error_estimate, &
relative_error,absolute_error) &
result(integral)
! f is the function we want to integrate:
interface
function f(x) result(f_x)
use Precision, only: wp
real(kind=wp), intent(in) :: x
real(kind=wp) :: f_x
end function f
end interface
real(kind=wp), intent(in) :: a,b ! The interval of integration
real(kind=wp), intent(out) :: error_estimate ! Estimate of error
! The desired errors (they are optional):
real(kind=wp), intent(in), optional :: relative_error,absolute_error
real(kind=wp) :: integral ! The result of the integration
...
end function AdaptiveIntegral
end module Numerical_Integration
It is important to point that in the module Precision it is defined
that wp=dp, so you need to use double precision in your main
program as well (this library only came in double precision). There will be
no examples given of how to call this routine. You should be able to read
the above specifications and call this function without any problems.
Just like the plotting routines in the FunGraphics module, the
above integration routine needs to be supplied with a user function to
integrate. In our case, this function will be related to
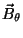 , since this is the integrand we need to integrate. Use the expression that
Mathematica gave you for
, since this is the integrand we need to integrate. Use the expression that
Mathematica gave you for
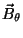 to write two functions,
say dBx and dBy, that have the same interface as the
function f in the routine AdaptiveIntegral (see above) and
return the x and z components of
to write two functions,
say dBx and dBy, that have the same interface as the
function f in the routine AdaptiveIntegral (see above) and
return the x and z components of
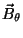 respectively.
These will accept
respectively.
These will accept 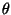 as an input argument (why?), but will need to
know the values of x and z. By placing the routines in a module, say
B_theta, and making x and z global public variables in this
module, the main program can set these values (say the user enters them)
before calling the routine AdaptiveIntegral, and all should work
well. Re-read the description of this methodology given in the last
worksheet so you understand how it works.
Now compile and run your program and evaluate the magnetic field at the same
point as you did in your Mathematica worksheet. Compare the two
results.
Once you make the above work, if you have time and will, you can plot
the magnetic field from within Fortran using the FunContourPlot2D
routine from the last worksheet. If you want some Fortran challenge, do this
and we will help you. One thing to carry in mind is that the plotting
routines accept only single precision arguments, while the integration
routines above accept only double precision variables. So you need to be
more careful this time than the usual REAL(KIND=wp) in all
declarations.
You will get extra credit applied toward your final exam if you do
this!
As usual, the ready-made files are in our class directory. Before you
compile your code, execute:
as an input argument (why?), but will need to
know the values of x and z. By placing the routines in a module, say
B_theta, and making x and z global public variables in this
module, the main program can set these values (say the user enters them)
before calling the routine AdaptiveIntegral, and all should work
well. Re-read the description of this methodology given in the last
worksheet so you understand how it works.
Now compile and run your program and evaluate the magnetic field at the same
point as you did in your Mathematica worksheet. Compare the two
results.
Once you make the above work, if you have time and will, you can plot
the magnetic field from within Fortran using the FunContourPlot2D
routine from the last worksheet. If you want some Fortran challenge, do this
and we will help you. One thing to carry in mind is that the plotting
routines accept only single precision arguments, while the integration
routines above accept only double precision variables. So you need to be
more careful this time than the usual REAL(KIND=wp) in all
declarations.
You will get extra credit applied toward your final exam if you do
this!
As usual, the ready-made files are in our class directory. Before you
compile your code, execute:
# source /classes/phy201/Integration.init
and then append a $ADQDvf90 (stands for adaptive quadrature with
VAST f90) to every compilation line. If you use the graphics modules as well
source the file SimpleGraphics.init as well and append a
$DISLINvf90 as well.



Next: About this document ...
Up: No Title
Previous: No Title
Aleksandar Donev
2000-12-12