


Next: About this document ...
Up: Electromagnetism with Fortran and
Previous: Electromagnetism with Fortran and
Subsections
In this worksheet, you should use both Mathematica and Fortran 90 to plot
the electric potential and field of a distribution of n charges with
different magnitudes qi placed in the xy plane at points
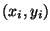 .
The number of charges, their magnitudes and their
positions can either be entered by the user or you can fix their values in
the program. For example, you could place four unit charges at the corners
of a unit square with alternating signs. Its your choice, but be consistent
between your Mathematica worksheet and Fortran 90 program, so you can
compare the solutions. Remeber that the potential of a single charge is,
.
The number of charges, their magnitudes and their
positions can either be entered by the user or you can fix their values in
the program. For example, you could place four unit charges at the corners
of a unit square with alternating signs. Its your choice, but be consistent
between your Mathematica worksheet and Fortran 90 program, so you can
compare the solutions. Remeber that the potential of a single charge is,
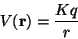 |
(1) |
while the electric field is given by:
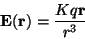 |
(2) |
Here bold letters denote a vector, while regular letters are scalars. For
this worksheet, just take K=1. Also remember that the potential and field
of a group of charges is the sum of the individual potentials and fields.
Store the magnitudes of the charges in an array (lists), and store their
positions in a two-dimensional array (nested list). For example:
q={1,-2};
r={{1,2},{0,-1}};
Now define a Mathematica function (operator) to evaluate the potential at a
given point (vector)
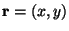 .
Try to invise an
operator that will work with any q and r.
Just to remind you, here is an example of defining an operator in
Mathematica that calculates the square of an expression x:
.
Try to invise an
operator that will work with any q and r.
Just to remind you, here is an example of defining an operator in
Mathematica that calculates the square of an expression x:
sqr[x_]:=x^2
You may also need a function to calculate the length of a vector
r
,
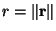 .
You can use, for example, a dot product (
.) to do this:
.
You can use, for example, a dot product (
.) to do this:
magnitude[r_]:=Sqrt[r.r]
Plot the electric potential both as a surface (Plot3D in
Mathematica) and as a contour plot (ContourPlot) and compare the
two. Which one is better and why? Try to make both plots look as nice as
possible. Then plot the electric field as a vector field (
PlotVectorField loaded with the package via <
< Graphics`PlotField`).
Plotting the potential in Fortran involves more work then doing it in
Mathematica. However, try to observe the possible advantages of Fortran. We
will not introduce new material in this worksheet. You will need to use
simple arrays extensively though, so review this material (sections 1.9.1,
1.9.2, 2.6.1, 2.6.2, 2.6.3, 2.6.4 and 2.6.9 in the manual. In particular,
try to understand the concept of array constructors, as these can
make your life much easier for this assignment). The positions of the
charges will be stored in a two-dimensional array (matrix), and this is the
first time you encounter these in this class. They are no different from
vectors, at least at this level of usage.
In the next three worksheets we will not introduce any new Fortran material.
We will in fact use all of the things that we learned with the error
function project to solve some numerical problems in electrostatics. Some of
the things you learned so far are essentials in Fortran 90 and you need to
understand them well. These include variable declaration and basic I/O, the
concept of a main program and what it does, what modules are and how we use
them to encapsulate (organize and protect) global (module) variables and
procedures, how to declare procedures and their arguments (this particularly
encompases understanding which data are private to a procedure and which are
global and why), how to declare and use simple one and two dimensional
(rank-1 and rank-2) arrays, and how to read the documentation (interfaces)
for a ready-made library and use the library to solve a problem. You may
find that additional Fortran 90 features (un)documented in the manual may
make life much easier, but it won't be necessary to use them.
The physics applications that we will explore in these final worksheets will
all have the same global structure for the Fortran code. The main
computational routines, be this plotting or numerical integration or
numerical solution of differential equations, will be ready-made and
provided for you as a very easy-to-use Fortran 90 module with good
documentation and examples. These mini libraries know nothing about physics,
they are computational libraries! If you actually want to learn how these
routines work and how to write them, take Numerical Analysis or PHY480.
Now, all of these ready-made routines will accept some input argument from
the user that contains the physics of the process. We have chosen to make
this a procedure (usually a FUNCTION) that calculates some physical
quantity (this is a frequent situation). For example, in today's worksheet
you will need to write a function V that calculates the electric potential
at a given point
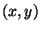 ,
next time you will need to write a
function that evaluates the Bio-Savart contribution to the magnetic field at
a given point, after that you will need to write a function that evaluates
the force on a particle moving in an electromagnetic field, etc.
Please review your basic electrostatics and magnetostatics for this before
coming to lab.
The main point is that this function that you will write will contain all
the relevant physics to the problem. As such, this function should be placed
in a separate module which should also contain in it the relevant physical
variables (such as charges, currents, fields, etc.) that this procedure will
need. Then the main program will USE this module and assign values
to these physical variables (say the user will enter them). You should
always make only those variables that both the procedure and the main
program access global (module) variables--the rest should be private to the
function or the main program. Finally, the main program will call the
calculation/plotting ready-made routines and print the results if necessary.
We hope this gives you an idea of how this works in Fortran.
Mathematica is a great tool, but most people use it without ever
understanding its inner workings and thus use it inefficently. But with
Fortran everything is transparent and you need to have a clear picture of
what and why you are doing. Finally, we should emphasize that we chose to
stick with the methodology outlined in this section in all of the remaining
worksheets not because it will always be the best choice, but simply
so that we do not overload you with many different strategies.
We will do the plotting in Fortran similarly to the way we did it in
Mathematica. In particular, you should make a new module and place a
function in it that gives the electrostatic potential at a certain point
,
next time you will need to write a
function that evaluates the Bio-Savart contribution to the magnetic field at
a given point, after that you will need to write a function that evaluates
the force on a particle moving in an electromagnetic field, etc.
Please review your basic electrostatics and magnetostatics for this before
coming to lab.
The main point is that this function that you will write will contain all
the relevant physics to the problem. As such, this function should be placed
in a separate module which should also contain in it the relevant physical
variables (such as charges, currents, fields, etc.) that this procedure will
need. Then the main program will USE this module and assign values
to these physical variables (say the user will enter them). You should
always make only those variables that both the procedure and the main
program access global (module) variables--the rest should be private to the
function or the main program. Finally, the main program will call the
calculation/plotting ready-made routines and print the results if necessary.
We hope this gives you an idea of how this works in Fortran.
Mathematica is a great tool, but most people use it without ever
understanding its inner workings and thus use it inefficently. But with
Fortran everything is transparent and you need to have a clear picture of
what and why you are doing. Finally, we should emphasize that we chose to
stick with the methodology outlined in this section in all of the remaining
worksheets not because it will always be the best choice, but simply
so that we do not overload you with many different strategies.
We will do the plotting in Fortran similarly to the way we did it in
Mathematica. In particular, you should make a new module and place a
function in it that gives the electrostatic potential at a certain point
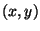 .
The interface of this function (the name is
irrelevant) should be:
.
The interface of this function (the name is
irrelevant) should be:
FUNCTION V(x,y) RESULT(U)
REAL(KIND=sp), INTENT(IN) :: x,y
REAL(KIND=sp) :: U
...Calculate U=V(x,y) here...
...Sum the potential contributions from each charge...
END FUNCTION V
It is up to you to devise a way of calculating the potential inside this
function. The best and recommended approach is to make arrays that will hold
the magnitudes and positions of the charges, just like we did in
Mathematica, and then sum the individual contributions to the potential from
each charge. To insure that you never divide by zero, add a small constant
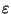 ,
called TINY(0.0_sp) in Fortran 90, to the
denominator in equations
,
called TINY(0.0_sp) in Fortran 90, to the
denominator in equations ![[*]](/misc/icons.gif/cross_ref_motif.gif) and
and ![[*]](/misc/icons.gif/cross_ref_motif.gif) .
This function V will need to know the positions and magnitudes of
the charges. Since these can not be passed to the procedure (because the
plotting routine described below only accepts functions with the above
interface), you should make these global (module) variables in the module
where you put the function V(x,y). That way the main program can
work with these arrays as well. Now, pass tthe function V as an
argument to the plotting routines described in the next section, which will
calculate this function at a grid of points and invoke the DISLIN graphics
library to render the plot.
After this works and you get what you consider to be a good plot of the
potential, move to plotting the electric field. You will need to make a
function, for example E, that returns the two components of the
electric field
E(x,y) for given x and y. The result should in
fact be an array of length 2, in the form (/Ex,Ey
/):
.
This function V will need to know the positions and magnitudes of
the charges. Since these can not be passed to the procedure (because the
plotting routine described below only accepts functions with the above
interface), you should make these global (module) variables in the module
where you put the function V(x,y). That way the main program can
work with these arrays as well. Now, pass tthe function V as an
argument to the plotting routines described in the next section, which will
calculate this function at a grid of points and invoke the DISLIN graphics
library to render the plot.
After this works and you get what you consider to be a good plot of the
potential, move to plotting the electric field. You will need to make a
function, for example E, that returns the two components of the
electric field
E(x,y) for given x and y. The result should in
fact be an array of length 2, in the form (/Ex,Ey
/):
FUNCTION E(x,y) RESULT(E_)
REAL(KIND=sp), INTENT(IN) :: x,y
REAL(KIND=sp), DIMENSION(2) :: E_
...Calculate E_=E(x,y) here...
END FUNCTION V
There is many possibilities for coding equations ![[*]](/misc/icons.gif/cross_ref_motif.gif) and
and ![[*]](/misc/icons.gif/cross_ref_motif.gif) in
Fortran, some faster than others, some more elegant than others. For those
that like trying new things, we would suggest reading section 2.6.5 and
2.6.6. Using array operations in Fortran 90, it is possible to code the
above formulas so they almost fully resemble the Mathematica coding, but
since the number of dimensions is fixed, faster solutions exist.
The first and most challenging task in this worksheet is to write the module
that will contain the function V(x,y). First, you need to decide what
variables this procedure will need other than its input arguments x and y
and decide on how you are going to represent these variables. Surely the
program will need to know the number of charges, their magnitudes and their
positions. The number of charges n_charges is a simple integer,
the magnitudes can be easily represented by a simple one-dimensional array
of real numbers q(n_charges), but the the positions of the charges
give you more room to experiment. For example, you can have two (three)
arrays holding the x and y coordinates of each charge,
x(n_charges) and y(n_charges), or you can merge these two into a
two-dimensional array r(2,n_charges), where the first row will be
the x and the second row the y coordinates.
You can make all the arrays either allocatable (in which case the main
program can do the allocation). If you want to make them of fixed size, make
sure that simply changing n_charges will be enough to work with a
different number of charges:
in
Fortran, some faster than others, some more elegant than others. For those
that like trying new things, we would suggest reading section 2.6.5 and
2.6.6. Using array operations in Fortran 90, it is possible to code the
above formulas so they almost fully resemble the Mathematica coding, but
since the number of dimensions is fixed, faster solutions exist.
The first and most challenging task in this worksheet is to write the module
that will contain the function V(x,y). First, you need to decide what
variables this procedure will need other than its input arguments x and y
and decide on how you are going to represent these variables. Surely the
program will need to know the number of charges, their magnitudes and their
positions. The number of charges n_charges is a simple integer,
the magnitudes can be easily represented by a simple one-dimensional array
of real numbers q(n_charges), but the the positions of the charges
give you more room to experiment. For example, you can have two (three)
arrays holding the x and y coordinates of each charge,
x(n_charges) and y(n_charges), or you can merge these two into a
two-dimensional array r(2,n_charges), where the first row will be
the x and the second row the y coordinates.
You can make all the arrays either allocatable (in which case the main
program can do the allocation). If you want to make them of fixed size, make
sure that simply changing n_charges will be enough to work with a
different number of charges:
INTEGER, PARAMETER :: n_charges=2 ! Change this later
REAL(KIND=wp), DIMENSION(n_charges) :: q ! This stays the same
...
Here is an outline of a possible module Charges:
MODULE Charges
...
PUBLIC
INTEGER :: n_charges ! The number of charges present
! In this program, q is of shape [n_charges],
! while r is of shape [2,n_charges]
REAL(KIND=wp), ALLOCATABLE, DIMENSION(:) :: q ! The magnitudes
REAL(KIND=wp), ALLOCATABLE, DIMENSION(:,:) :: r ! The positions
CONTAINS
! This function gives the potential at the point <x,y> by
! summing over the contributions from the individual charges:
FUNCTION V(x,y) RESULT(U)
REAL(KIND=wp), INTENT(IN) :: x,y
REAL(KIND=wp) :: U
...
END FUNCTION V
! This function gives the electric field at the point <x,y>:
FUNCTION E(x,y) RESULT(E_)
REAL(KIND=wp), INTENT(IN) :: x,y
REAL(KIND=wp), DIMENSION(2) :: E_
...
END FUNCTION E
...
END MODULE Charges
We have not given the body of the function V(x,y) and
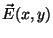 here.
There are a lot of options. You know that you need to perform a sum over the
contributions from different charges (probably using a DO loop).
You can calculate the magnitude (distance) r appearing in
here.
There are a lot of options. You know that you need to perform a sum over the
contributions from different charges (probably using a DO loop).
You can calculate the magnitude (distance) r appearing in
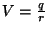 in different ways. For example, here is the distance from the observation
point (x,y) to the
in different ways. For example, here is the distance from the observation
point (x,y) to the
 charge:
charge:
dr = SQRT( (x-r(1,i))**2 + (y-r(2,i))**2 ) + TINY(0.0_wp)
In the main program, you will need to assign values to the magnitudes and
positions of the charges. For the magnitudes, you can use element-by-element
assignment (see below) or array-constructors. For the positions of the
charges, you can first set all of them to zero, and then do an
element-by-element assignment to the non-zero entries (see below). You can
also use array constructors for the positions as well. However, array
constructors always return rank-1 arrays. You can use the intrinsic function
RESHAPE to make this a rank-2 array:
r = RESHAPE( SOURCE = (/ (/1.0,2.0/), (/-1.0,0.0/), &
(/-.5,-1.0/), (/2.0,-1.0/) /), &
SHAPE = (/2,n_charges/) )
Other approaches include letting the user enter these with READ (in
column-wise order for rank-2 arrays) or assigning random numbers (for 10
charges this may be a choice):
CALL RANDOM_NUMBER(r) ! Intrinsic function for random numbers
For example, one possible strategy is:
PROGRAM Electrostatics
USE Charges
...
n_charges=2
ALLOCATE(q(n_charges),r(2,n_charges))
! A dipole:
q(1)=1.0_wp
q(2)=-1.0_wp
! Positions:
r=0.0_wp
r(1,1)=-1.0_wp
r(1,2)=1.0_wp ! What are the positions of the charges? Picture?
...
CALL FunPlot3D(f_xy=V,...)
...
END PROGRAM Electrostatics
After these values have been assigned, the main program needs to call the
plotting routines from the FunGraphics module and pass the
functions V and  from the module Charges as arguments.
The examples in the documentation are sufficient help for this.
Please ask your TA or instructor if this is unclear. The remaining two
worksheets will follow the exact same strategy, only with different physics.
Understanding this one one will save us all time and frustrations, even if
you need an extra week to finish it.
In the last worksheet you learned how to make a simple 2D plot with the
SimpleGraphics module. In 3D, making all the required arrays
manually and assigning their values is more cumbersome, so we made a new
module with pre-compiled routines that will plot a function instead of an
array, thus simplifying the usage significantly. This FunGraphics
module is documented in:
http://computation.pa.msu.edu/phy201/FunGraphics.html
You should now get a feeling of how these routines work and be able to use
the routines FunPlot3D and/or FunPlotContour (we recommend
the one you determined to be nicer in your Mathematica code) to plot
the potential V(x,y) and the routine FunVectorPlot2D to plot the
electric field. The example given in the above wepage,
FunPlot_3D.f90, is very helpful. The executable of the example is in the
file /classes/phy201/FunPlot_3D.x, and the code is also there. You
only need to change some of the numbers and pass the functions you just made
as an argument, as in:
from the module Charges as arguments.
The examples in the documentation are sufficient help for this.
Please ask your TA or instructor if this is unclear. The remaining two
worksheets will follow the exact same strategy, only with different physics.
Understanding this one one will save us all time and frustrations, even if
you need an extra week to finish it.
In the last worksheet you learned how to make a simple 2D plot with the
SimpleGraphics module. In 3D, making all the required arrays
manually and assigning their values is more cumbersome, so we made a new
module with pre-compiled routines that will plot a function instead of an
array, thus simplifying the usage significantly. This FunGraphics
module is documented in:
http://computation.pa.msu.edu/phy201/FunGraphics.html
You should now get a feeling of how these routines work and be able to use
the routines FunPlot3D and/or FunPlotContour (we recommend
the one you determined to be nicer in your Mathematica code) to plot
the potential V(x,y) and the routine FunVectorPlot2D to plot the
electric field. The example given in the above wepage,
FunPlot_3D.f90, is very helpful. The executable of the example is in the
file /classes/phy201/FunPlot_3D.x, and the code is also there. You
only need to change some of the numbers and pass the functions you just made
as an argument, as in:
CALL FunPlot3D(f_xy=V,xy_range=(/x_min,x_max,y_min,y_max/),...)
The same goes for the contour and vector plot as well. Play with the plots
until they at least partially resemble the Mathematica plots and
compare the two. If you need more time to finish this worksheet, talk to us.
Notice that we do not give a lot of pseudocode here. This is because you
should already have an understanding of how to make a module and encapsulate
functions in it and then USE the module in a program. The example
file erf_fun_plot.f90 in /classes/phy201 solves last
week's assignment using the FunGraphics module and can be very
helpful to look at. The executable solution to this worksheet is in the file
charges.x. The procedure for compiling and linking the program is
the same as in the last worksheet.
Notice how we have used all the things we learned so far (with the error
function project), only now in a physics context. Tell us how you feel about
these worksheets!



Next: About this document ...
Up: Electromagnetism with Fortran and
Previous: Electromagnetism with Fortran and
Aleksandar Donev
2000-12-12