


Next: About this document ...
Up: No Title
Previous: No Title
Subsections
In this worksheet you will continue the work started in worksheet
1--evaluating the error function of a real or complex number using
truncated power series. You will reuse much of the code written before. Use
the Copy-Paste features of the text editor to speed the process.
The main feature of your new program should be that it is well structured
and organized. Two main features of Fortran will help you in that,
modules and procedures (functions and subroutines). Read
sections 2.1 and 2.4 carefully.
In the next worksheet we will introduce arrays and file I/O, and plot the
error function using these new Fortran features.
The main defficiency of the code you wrote in the first worksheet was that
the error function was not really a function. What we really want is to have
a function called Erf which we can simply envoke like the other
intrinsic Fortran functions, as in:
WRITE(*,*) Erf(1.0_wp)
Your first task therefore is to convert the previous code for evaluating the
error function into a procedure, preferably a FUNCTION. This
implies that x needs to be a dummy argument to this procedure, and the
result should be
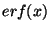 .
You should have two different procedures,
one for REAL and one for COMPLEX arguments
.
You should have two different procedures,
one for REAL and one for COMPLEX arguments![[*]](/misc/icons.gif/foot_motif.gif) . For example, the REAL function might start as:
. For example, the REAL function might start as:
FUNCTION ErfOfReal(x) RESULT(erf)
REAL(KIND=wp), INTENT(IN) :: x
REAL(KIND=wp) :: erf
...
END FUNCTION ErfOfReal
The body of the function should be very similar to your previous code.
However, there are several important differences. First, remove all I/O
statements (such as WRITE). The user may call this function many
times (in large calculations) and does not want to see huge printouts. All
the printing should be done from the main program, while the procedure
should provide enough information to the caller so that a suitable action
can be taken in case of error, for example.
Now we have to introduce modules to make the above procedure complete. In
Fortran 90, all procedures should be packaged in modules. So make a new
MODULE in which you will place the above routine. It is also
advisable that any data shared by several procedures in the module and/or
the main program, such as the precision variable wp, the desired
precision
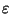 ,
or the maximum number of iterations, be placed in
the module as module variables. That way all the program units that
USE the module and all the procedures inside the module will be able to
manipulate these variables. Remember that procedure declarations come in the
module after a CONTAINS statement.
Finally, a tricky point arises with the possibility that the truncated
series does not converge to within the desired accuracy. Two approaches are
used to flag such an error. The first makes the above FUNCTION into
a pseudo subroutine, and returns a logical variable which tells whether the
summation converged or not. This is essentially an approach widely used in C:
,
or the maximum number of iterations, be placed in
the module as module variables. That way all the program units that
USE the module and all the procedures inside the module will be able to
manipulate these variables. Remember that procedure declarations come in the
module after a CONTAINS statement.
Finally, a tricky point arises with the possibility that the truncated
series does not converge to within the desired accuracy. Two approaches are
used to flag such an error. The first makes the above FUNCTION into
a pseudo subroutine, and returns a logical variable which tells whether the
summation converged or not. This is essentially an approach widely used in C:
FUNCTION ErfOfReal(x, erf) RESULT(converged)
REAL(KIND=wp), INTENT(IN) :: x
REAL(KIND=wp), INTENT(OUT) :: erf
LOGICAL :: converged
...
IF(...) THEN
converged=.TRUE. ! If converged
ELSE
converged=.FALSE. ! If not converged
END IF
...
END FUNCTION ErfOfReal
This approach is elegant and allows better modular approach, but has some
deficiences (such as an extra argument passed each time). Another simpler
approach that is used often in scientific programming is to make a global
(module) logical variable, called a flag, and set the flag to .FALSE.
(raise the flag in case of error). Choose whichever approach you prefer,
but make sure you understand both. With the second approach your module
might look like:
MODULE Erf_Series
PUBLIC ! For now, use this statement
INTEGER, PARAMETER :: sp=KIND(0.0E0), dp=KIND(0.0D0)
INTEGER, PARAMETER :: wp=sp ! Or wp=dp
INTEGER, PARAMETER :: max_iterations=100
REAL(KIND=wp) :: epsilon
LOGICAL :: converged=.TRUE.
...
CONTAINS
FUNCTION ErfOfReal(x) RESULT(erf)
...
END FUNCTION ErfOfReal
FUNCTION ErfOfComplex(x) RESULT(erf)
...
END FUNCTION ErfOfComplex
END MODULE Erf_Series
The main program will now be much shorter, since all the computation is in
the above routines. The main program should prompt the user to enter x,
then call the function ErfOrReal or ErfOfComplex, and
print the result. It should also check if an error occured and print a
message. For example:
PROGRAM Erf_Numerical
USE Erf_Series
...
REAL(KIND=wp) :: x, erf ! These are actual arguments
...
erf=ErfOfReal(x) ! Or complex
IF(.NOT.converged) &
WRITE(UNIT=*,FMT=*) ``The result below has not converged''
WRITE(UNIT=*,FMT=*) erf
...
END PROGRAM Erf_Numerical
To make the above program fully Fortran 90 powered, one can use
generic interfaces (these are not covered in the manual as they are more
advanced features). If you feel like you learned enough in this worksheet
already, then do not go throught his section!
In the above program we could not call ErfOfReal with a complex
argument. What we want is a function like SIN, which can be called
with an arbitrary precision/type of the argument. To do this, one needs to
write into the module procedures for different combinations of types and
precisions (kinds) of the arguments, and than make a wrapper generic routine
that encompasses all different cases. In the example above, this is done by
putting the following INTERFACE in the body of the module (before
CONTAINS):
INTERFACE Erf
MODULE PROCEDURE ErfOfReal
MODULE PROCEDURE ErfOfComplex
... ! Other types of arguments
END INTERFACE Erf
Now in the main program one can write:
WRITE(*,*) Erf(1.0_wp) ! REAL argument
WRITE(*,*) Erf((1.0_wp,0.0_wp)) ! COMPLEX argument
Final note should be made that the above files are in double precision and
were compiled with f90-vast. However, as you should have noticed,
when you tried to set wp=dp and print the results, they still print with 7-8
digits. This is because in g77 an explicit format descriptor
(other than FMT=*) is needed to print these correctly. See section
1.6.3 in the manual for details. For example, FMT=``(D21.15)'' can
be used in this case.
A quick note about something that came up in class and the manual also
emphasizes: Include the statement,
IMPLICIT NONE
in all your programs and modules after any potential USE
statements (which should come first always). This way the compiler will
check and make sure you have declared all your variables correctly.
By now you probably realized that you need to put all modules USEd
by other modules at the top of the file, before they are USEd. This
is because the compiler needs to compile these first, generate the needed
information and then USE it. In larger projects, like our now
month-old error function series is slowly becoming, it is wise to keep each
module in a separate file and compile it individually. Although it is not
neccessary you do this, it will be much easier and you will avoid a lot of
copying and pasting and repetitive work
This is how that is done: Assume we have a file Module.f90 which
contains a module used in the main program or another module that is in the
file Program.f90. First, just compile, and don't produce any
executables, (the switch is -c) the module file:
> f90-vast -c Module.f90 -o Module.o
This will produce something called an object file Module.o
from all the subroutines in the module and make a file in the current
directory Module.vo with information about the module. These files
will be used by all compilations that use the module. Make sure you stay in
the same directory if you like your life to be easier. Now, you can compile
the executable, and link the produced object file:
> f90-vast Program.f90 Module.o -o Program.x
Compiler usage is not trivial, especially with Fortran 90, but the same
principles apply to any programming language, so it is well worth your time
to play with this compiler!



Next: About this document ...
Up: No Title
Previous: No Title
Aleksandar Donev
2000-12-12