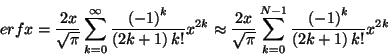Next: About this document ...
Up: Numerical Calculation of
Previous: Numerical Calculation of
Subsections
In this worksheet, you will write a Fortran program that will evaluate the
error function of a real or complex number. You will use
 to check your answers, because it has this function built in.
For small argument x, a good and efficient way to evaluate
to check your answers, because it has this function built in.
For small argument x, a good and efficient way to evaluate
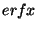 is to use the truncated power series:
is to use the truncated power series:
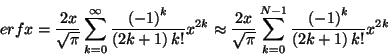 |
(2) |
Equation ![[*]](/misc/icons.gif/cross_ref_motif.gif) is a so called alternating power series and is
theoretically convergent for all x. If one truncates the series at some
high order term N-1, the error
is a so called alternating power series and is
theoretically convergent for all x. If one truncates the series at some
high order term N-1, the error
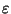 that is made is smaller the
first discarded term:
that is made is smaller the
first discarded term:
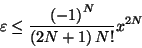 |
(3) |
If x is significantly larger than 1 (5 or larger) that the series in
![[*]](/misc/icons.gif/cross_ref_motif.gif) will converge very slowly. Other series expansions (asymptotic
series) can be used in that case. You need not worry about this. If
will converge very slowly. Other series expansions (asymptotic
series) can be used in that case. You need not worry about this. If
 ,
assume that
,
assume that
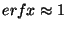 and return this value
without calculating the sum!
The main characteristic of this first ``real'' Fortran code that you will
write is that it will be an unstructured program--there will be no modules
or procedures. For this assignment, you should read sections 1.1-1.4,1.6-1.7
(exclude 1.6.4) in the FORTRAN 77 part of the manual and sections 2.1-2.3
(exclude 2.2.3) and 2.5 in the Fortran 90 manual. Please make sure you
have read through these carefully before coming to lab--examples can be
found there and will not be given to you unless they have new information in
them.
You will receive more information on editing and compiling programs with a
new Fortran 90 compiler that we just obtained, as well as some UNIX basics
in class. You will be expected to use the more modern Fortran 90 syntax when
applicable.
In worksheet 1 you learned how to evalute a sum of the form
and return this value
without calculating the sum!
The main characteristic of this first ``real'' Fortran code that you will
write is that it will be an unstructured program--there will be no modules
or procedures. For this assignment, you should read sections 1.1-1.4,1.6-1.7
(exclude 1.6.4) in the FORTRAN 77 part of the manual and sections 2.1-2.3
(exclude 2.2.3) and 2.5 in the Fortran 90 manual. Please make sure you
have read through these carefully before coming to lab--examples can be
found there and will not be given to you unless they have new information in
them.
You will receive more information on editing and compiling programs with a
new Fortran 90 compiler that we just obtained, as well as some UNIX basics
in class. You will be expected to use the more modern Fortran 90 syntax when
applicable.
In worksheet 1 you learned how to evalute a sum of the form
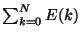 ,
where E(k) is some expression depending on k, using
Fortran:
,
where E(k) is some expression depending on k, using
Fortran:
sum=E(0)
DO k=1,N
sum=sum+E(k)
END DO
The only difference between this worksheet and the previous one is that the
expression to sum is more complicated. Complication comes because of the
presence of a factorial, which is not a built in function in Fortran.
However, even if there were a factorial function in Fortran, the best way to
evaluate E(k) is not to directly compute
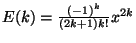 .
Rather, you can use the following recursive
relation (which is very easy to derive from eq.
.
Rather, you can use the following recursive
relation (which is very easy to derive from eq.![[*]](/misc/icons.gif/cross_ref_motif.gif) ) giving the ratio <tex2htmlcommentmark>
R(k) of two consecutive terms in the power series:
) giving the ratio <tex2htmlcommentmark>
R(k) of two consecutive terms in the power series:
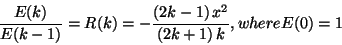 |
(4) |
Therefore, one can compute the expression E(k) with the following
simple loop:
expression=E(0)
DO k=1,N
expression=expression*R(k)
END DO
Notice that we already needed the same loop to do the summation. So in fact
we can merge the two DO loops into one loop from k=1 to k=N. Do
not forget to initialize the sum to the zeroth-order term
sum=E(0)=1. Look
through the formulas given above to see what equations you need to put in
the loop for calculating E(0) and R(k).
One issue was saliently forgotten in the discussion above. What should the
value of N be? You might say 100 terms should be enough to calculate the
sum with sufficient accuracy. Try this for different values of x.
But the efficient and preferred approach is to calculate at each step of the
DO loop an estimation of the truncation error as the value of the
first discarded value, given in equation ![[*]](/misc/icons.gif/cross_ref_motif.gif) . To do this, use an
infinite DO loop (section 2.5.2) of the manual and at each
iteration calculate the absolute value of the next term to be added,
. To do this, use an
infinite DO loop (section 2.5.2) of the manual and at each
iteration calculate the absolute value of the next term to be added,
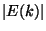 .
EXIT the loop if this value is smaller than a
certain precision
.
EXIT the loop if this value is smaller than a
certain precision
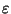 .
Most programs like this also should contain a guard against runaway endless
loops. If the number of iterations becomes larger than a certain maximal
number of iterations, you should exit the loop and print an error message.
For example:
.
Most programs like this also should contain a guard against runaway endless
loops. If the number of iterations becomes larger than a certain maximal
number of iterations, you should exit the loop and print an error message.
For example:
INTEGER, PARAMETER :: max_iterations=100 ! Max # of iterations
REAL(KIND=wp) :: epsilon ! Error allowed
...
k=0
Summation: DO
k=k+1
... ! Calculate E(k)
IF( ABS(E(k)) < epsilon ) THEN
WRITE(UNIT=*,FMT=*) ''Convergence was achieved!''
EXIT Summation
ELSE IF( k >= max_iterations ) THEN
WRITE(UNIT=*,FMT=*) ''Convergence not achieved!''
STOP ! Or EXIT if you can figure out how?
ELSE
... ! Calculate the sum here
END IF
END DO
Let the user enter the value of x and and print the result on the screen.
Compare the answer to what Mathematica gives.You will find
information on how to write algebraic expressions in Fortran in section 1.4.
Sections 1.3 and 2.2.1 on variables are essential to understand as well
since everything in Fortran is about variables. You will also need to
understand in detail DO and IF constructs, described in
sections 1.7.1, 1.7.2 and 2.5.2. The function ABS gives the
absolute value (modulus) of a number.
Also, look in section 2.2.2 to see how you can easily and efficiently
declare the precision--single (4 bytes, 7 digits) or double precision (8
bytes, 15 digits) for your REAL or COMPLEX variables using
parametrized kind values. We expect to see a KIND=wp attribute in
all declarations of floating-point numbers. Then it is very easy to change
the precision of the program variables by simply changing the value of the
kind integer wp. Fortran works with complex numbers in the exact
same way as with real numbers, so you shouldn't need to change anything in
your program but switch REAL to COMPLEX in the declaration
part. Save both versions of the program if you finish on time.
In the next worksheet we will significantly improve the design of this
program by packaging and structuring the program and we will also use the
program to actually plot the error function.
We now have a Fortran 90 educational compiler that you can use on
gauss.pa.msu.edu. Please use this compiler only for this class and
work related to it! This compiler is envoked in the same way as g77
, and is called f90-vast. Suffix your files with the extension
.f90, and preferably your executables with .x. For example:
> f90-vast YourProgram.f90 -o YourProgram.x
This compiler translates Fortran 90 programs into g77 programs.
Remember that Fortran 90 has free-form syntax, so you do not need to worry
about counting columns and spaces.
Compiled executables for worksheets can be found in the public directory
/classes/phy201/ for our class on gauss. All solutions, examples
and libraries will be put in this location, so explore it every now and
then! Also, remember to ask your instructor or TA when you need help.



Next: About this document ...
Up: Numerical Calculation of
Previous: Numerical Calculation of
Aleksandar Donev
2000-12-12