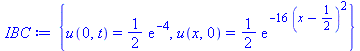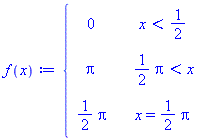Numerical Solutions of PDEs using PDEtools in Maple 

Aleksandar Donev, Courant Institute 

This is largely based on examples in the excellent Maple documentation 

Shock formation in Burger's equation  

>	PDE := diff(u(x, t), t) + (diff(u(x, t), x))*u(x, t) = 0;

 

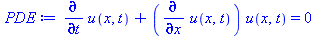(1)

 

>	IBC := {u(0, t) = (1/2)*exp(-4), u(x, 0) = (1/2)*exp(-16*(x-1/2)^2)};

 

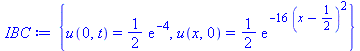(2)

 

>	pds := pdsolve(PDE, IBC, numeric, time = t, range = 0 .. 2, spacestep = 1/256, timestep = 1/60);

 

(3)

 

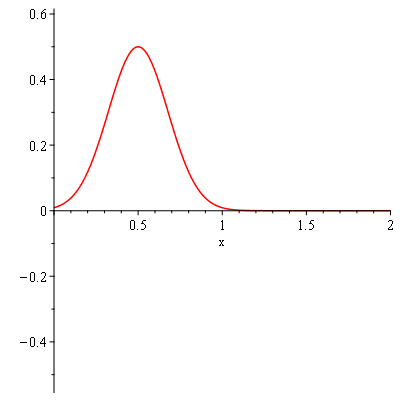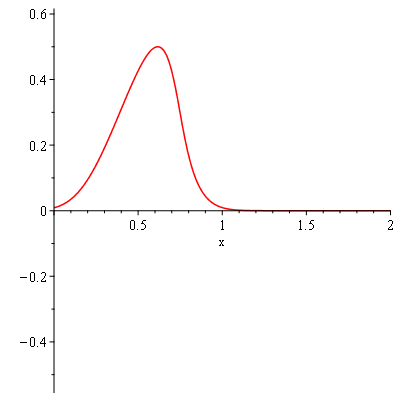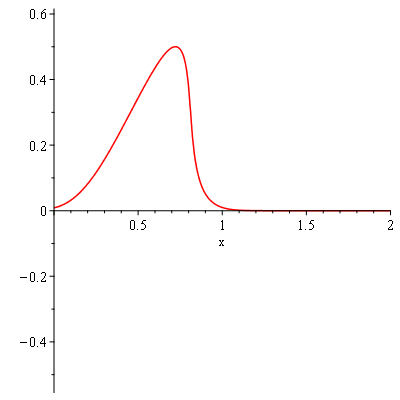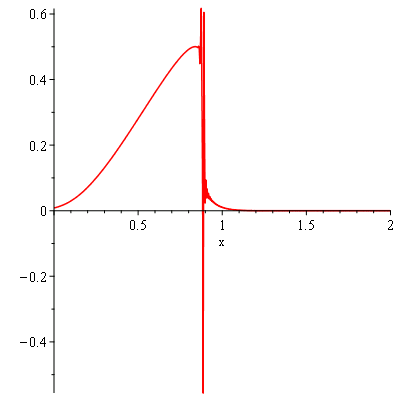
>	pds:-animate(t = 0..0.70, frames = 31); # Shock forms around t~0.68

 

 

Warning, could not compute solution for t>.683333333333335: Newton iteration is not converging

 

>

 

Heat equation in 1D with homogeneous Dirichlet BCs 

>	restart: with(PDEtools):

 

>

k:=1:

 

>	PDE:=diff(u(x, t), t) = k*diff(u(x, t), x, x);

 

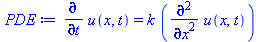(4)

 

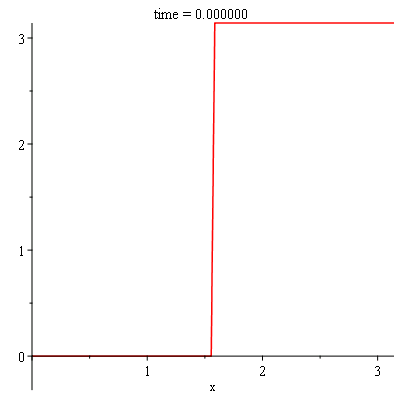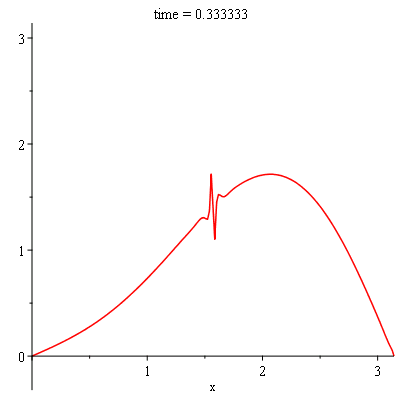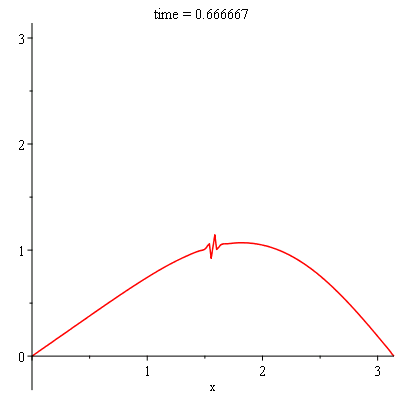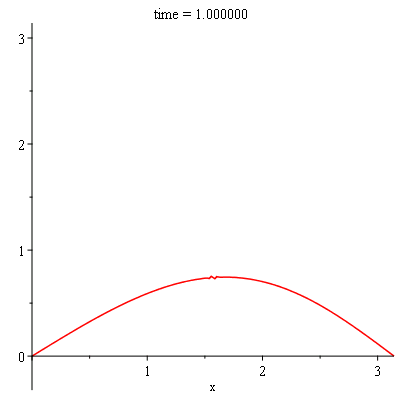
>	ICs:={u(0, t) = 0, u(Pi, t) = 0, u(x,0) = f(x)};

 

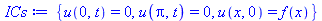(5)

 

>	f(x):=piecewise(x<1/2,0,x>Pi/2,Pi,x=Pi/2,Pi/2);

 

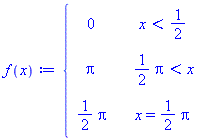(6)

 

>	sol:=pdsolve(PDE, ICs, numeric, time = t, range=0..Pi):

 

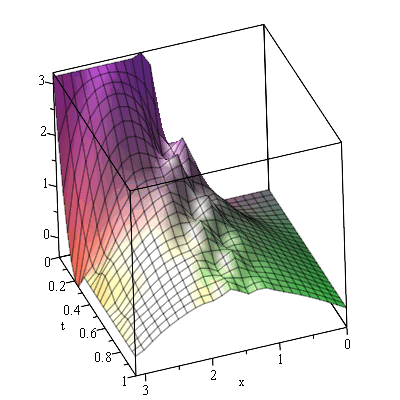
By default Maple uses too few points in the x direction and we get a rough solution that is not correct 

>	sol:-plot3d(t = 0 .. 1, x = 0 .. Pi, axes = boxed);

 

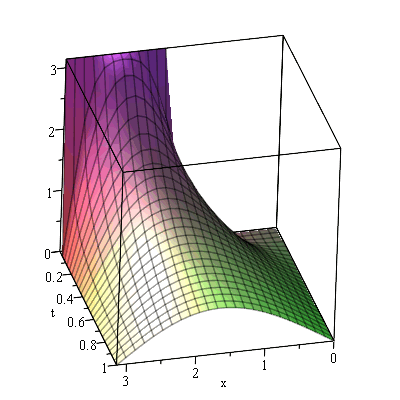
So let's increase the number of points manually 

>	sol:=pdsolve(PDE, ICs, numeric, time = t, range=0..Pi,'spacestep'=Pi/200);

 

(7)

 

>	sol:-plot3d(t = 0 .. 1, x = 0 .. Pi, axes = boxed);

 

>	sol:-animate(t = 0..1, frames = 100, title = "time = %f");

 

In order to get a non-oscillatory and physically-sensible solution we need to decrease both the space and time step size: 

>	sol:=pdsolve(PDE, ICs, numeric, time = t, range=0..Pi,'spacestep'=Pi/100, 'timestep'=0.002);

 

(8)

 

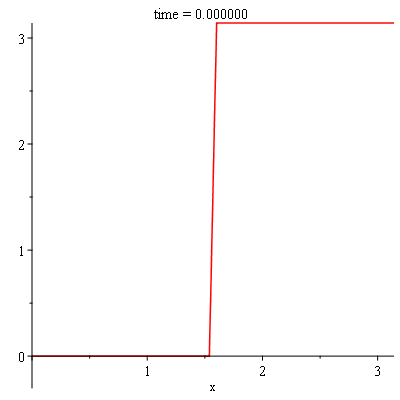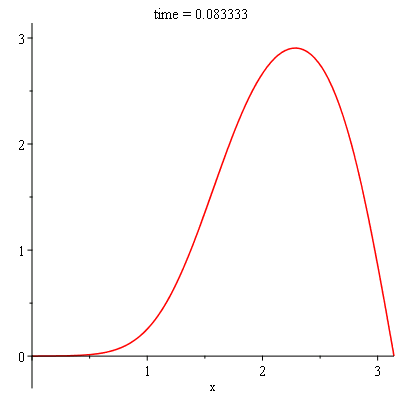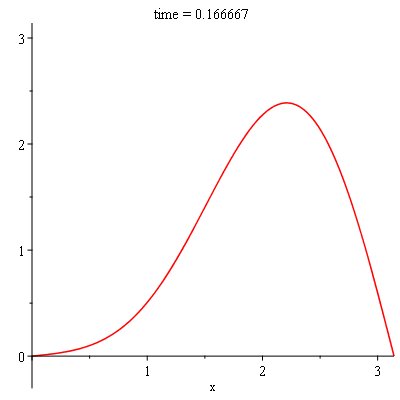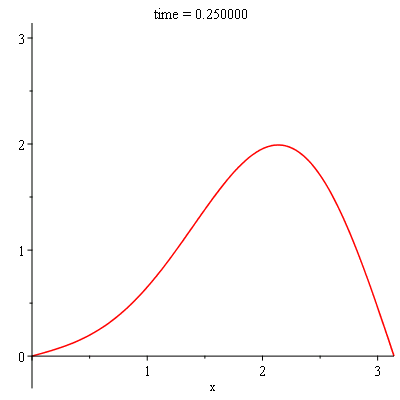
>	sol:-animate(t = 0..0.25, frames = 100, title = "time = %f");

 

Solitons in the KdV equation 

>	restart: with(PDEtools):

 

>	KdV:= diff(u(x,t),t) + u(x,t)*diff(u(x,t),x) + delta^2*diff(u(x,t),x$3) = 0;

 

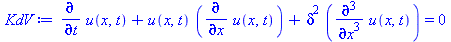(9)

 

>	delta:=0.022:

 

We impose periodic BCs on the domain [0..L=10] 

>	bc:={u(L,t)=u(0,t), D[1](u)(L,t)=D[1](u)(0,t), D[1$2](u)(L,t)=D[1$2](u)(0,t)};

 

(10)

 

>

L:=2:

 

>	ic:={u(x,0)=exp(-9*(x-1/2)^2)}:

 

>	sol_new:=pdsolve(KdV, bc union ic, numeric, spacestep=0.01, timestep=0.01);

 

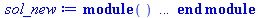(11)

 

>	sol_new:-animate(u(x,t), t=0..2, frames=100,color=blue,thickness=3,gridlines=true,title=`Emergence of solitons`,axes=boxed);

 

Error, (in pdsolve/numeric/animate) unable to compute solution for t>HFloat(0.0): Newton iteration is not converging

 

Apparently in some previous version of Maple this worked and produced the animation 

>

 

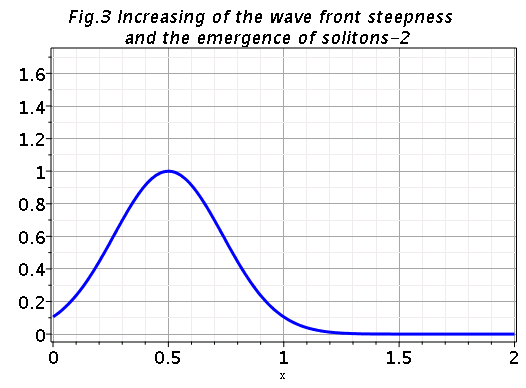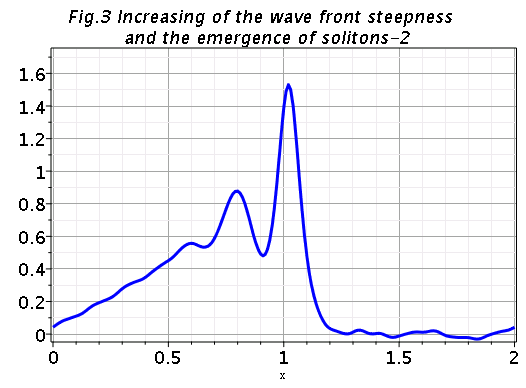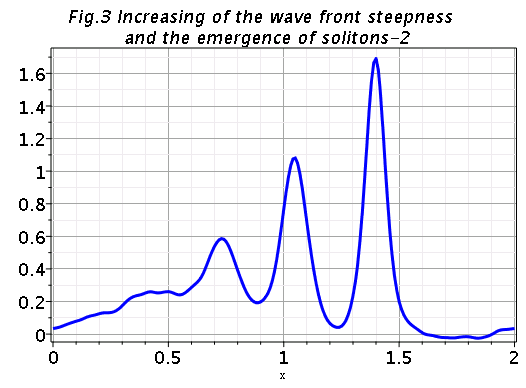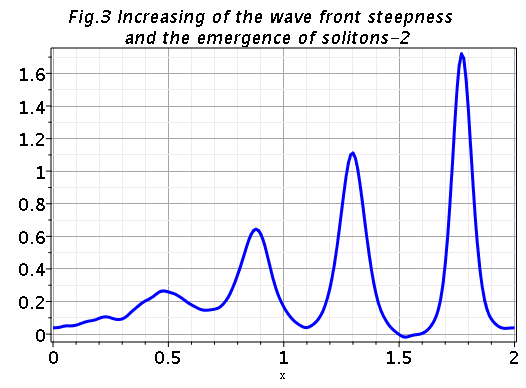What we are finding is that numerical solutions are quite tricky and sensitive and we better first understand what the methods do and try to solve these equations ourselves...let's switch to Matlab for that and do some theory first.