


Next: About this document ...
Up: No Title
Previous: Solution in Mathematica
Subsections
The Fortran solution to this problem will of course take some more efford.
You should write a program or better yet a procedure that uses the Euler
method to integrate a first order IVP of the form ![[*]](/misc/icons.gif/cross_ref_motif.gif) . Assume that
the function
. Assume that
the function 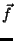 already exists and will be passed as an argument
along with number of unknowns n_unknowns in the dependent variable
already exists and will be passed as an argument
along with number of unknowns n_unknowns in the dependent variable
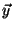 (in our case this is 6--3 coordinates and 3 velocities), the
number of time steps n_points to take and output the solution at,
the initial conditions x0 and y0, as well as the step size
dx:
(in our case this is 6--3 coordinates and 3 velocities), the
number of time steps n_points to take and output the solution at,
the initial conditions x0 and y0, as well as the step size
dx:
MODULE IVPSolve
USE Precision
...
SUBROUTINE Euler(f,y,n_unknowns,n_points,dx,x0,y0)
! The function f is passed as an argument:
INTERFACE
SUBROUTINE f(x,y,y_prime,n_unknowns)
USE Precision
INTEGER n_points
REAL(KIND=wp) :: x
REAL(KIND=wp), DIMENSION(n_unknowns) :: y, y_prime
END SUBROUTINE f
END INTERFACE
INTEGER :: n_unknowns,n_points
! Upon exit, this array should contain the solution
REAL(KIND=wp), DIMENSION(n_unknowns,n_points) :: y
REAL(KIND=wp) :: dx, x0 ! Step size and initial x
REAL(KIND=wp), DIMENSION(n_unknowns) :: y0 ! Initial y
...
...Declare any needed local variables here...
...Initialize variables for the DO loop...
DO i=1,n_points-1
...Calculate x here in steps of dx starting at x0...
CALL f(x,y(:,i),y_prime,n_unknowns)
y(:,i+1)=y(:,i)+y_prime*dx ! Euler's method
...
END DO
...
END SUBROUTINE Euler
END MODULE IVPSolve
Feel free to use any other approach. There is ample room for improvement in
the above scheme. For example, why output the solution at every time step,
and not every desired n_output steps? This will save on storage,
especially if n_points is very large. Also, those that feel up to
it can try coding a more sophisticated algorithm, such as Runge-Kutta and
ask for assistance if needed (you can use the file RK4.f90 as a
template).
It may be wise to first test your Euler routine on a simple case,
such as a simple harmonic oscillator,
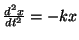 ,
by
printing (or plotting) your solution to verify correctness. It will then be
one more step to modify the function
,
by
printing (or plotting) your solution to verify correctness. It will then be
one more step to modify the function 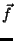 to reflect the problem of the
motion of a particle in an electromagnetic field. The strategy is the same
as usual. Make a separate module in which you will place
to reflect the problem of the
motion of a particle in an electromagnetic field. The strategy is the same
as usual. Make a separate module in which you will place 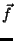 ,
and make
any physical parameters it may use, such as E0 and B0, public
module variables, so that the main program can set their values later on. We
leave it up to your ingenuity to code the vector expressions appearing in
eq.
,
and make
any physical parameters it may use, such as E0 and B0, public
module variables, so that the main program can set their values later on. We
leave it up to your ingenuity to code the vector expressions appearing in
eq. ![[*]](/misc/icons.gif/cross_ref_motif.gif) as you wish. We recommend using Mathematica to help you
in simplifying the expressions before coding them in Fortran.
Your main program should as usual first set the values of the physical
parameters in the problem. Simply choose one of the cases you analyzed in
Mathematica. Then call the integration routine Euler to
obtain the approximate solution.
The module SimpleGraphics has been supplemented with a rouine for
plotting points in 3D, Plot3D. The documentation in,
http://computation.pa.msu.edu/phy201/SimpleGraphics.html
contains the calling interface and an example. So a simple,
as you wish. We recommend using Mathematica to help you
in simplifying the expressions before coding them in Fortran.
Your main program should as usual first set the values of the physical
parameters in the problem. Simply choose one of the cases you analyzed in
Mathematica. Then call the integration routine Euler to
obtain the approximate solution.
The module SimpleGraphics has been supplemented with a rouine for
plotting points in 3D, Plot3D. The documentation in,
http://computation.pa.msu.edu/phy201/SimpleGraphics.html
contains the calling interface and an example. So a simple,
CALL Plot3D(x=y(4,:),y=y(5,:),z=y(6,:),...)
will plot the orbit of the particle in Cartesian space. The executable
solution to this assignment is in our class directory. Look at it!
There are many publicly available sophisticated Fortran libraries for
solving IVP's. In Fortran 90, such a library is RKSUITE90, which
implements adaptive Runge-Kutta methods. This library, or its FORTRAN 77
counterpart RKSUITE, are by no means easy to use, so we have again
made a wrapper routine, ODESolve in the module ODE, found
in our class directory. The interface for the routine is:
subroutine ODESolve(f,n_eq,x_range,n_points,y0,x,y,relerr,abserr)
interface
subroutine f(x,y,dy)
integer, parameter :: wp=kind(0.0D0)
real(kind=wp), intent(in) :: x
real(kind=wp), dimension(*), intent(in) :: y
real(kind=wp), dimension(*), intent(out) :: dy
end subroutine f
end interface
integer, intent(in) :: n_eq ! Number of unknowns
! The range of values to solve in (as in NDSolve)
! Thus x_range(1)=x0
real(kind=wp), dimension(2), intent(in) :: x_range
integer, intent(in) :: n_points ! Number of output points
real(kind=wp), dimension(n_eq), intent(in) :: y0 ! Initial y
! If you need them (for plotting), you can get the
! values of x for which the solution was outputed.
! But note that x=(/(x0+(i-1)*dx,i=1,n_points)/) always:
real(kind=wp), dimension(n_eq), intent(out), optional :: x
real(kind=wp), dimension(n_eq,n_points) :: y ! The solution
real(kind=wp), intent(in) :: relerr ! Desired relative error
! The absolute error is optional:
real(kind=wp), dimension(n_eq), intent(in), optional :: abserr
end subroutine ODESolve
Looks complicated? Not at all. Take a look at the example
Harmonic.f90 in our class directory. To compile programs that use this
module, first do a (not neccessary if your PC has been recently restarted),
# source /classes/phy201/ODE.init
and then append a $ODEvf90 to your compilation line. Notice that
this routine requires using double precision numbers, while the plotting
routines require single-precision values. Conversion will be neccessary!



Next: About this document ...
Up: No Title
Previous: Solution in Mathematica
Aleksandar Donev
2000-12-12