Is $0 \in \mathbb{N}$? Are constant functions increasing? How do you pronounce LaTeX? What the **** is a tensor?
From basic arithmetic to advanced real analysis, we mathematicians can't seem to agree on anything. The Mathematical Conventions Survey (MCS) aimed to highlight this while simultaneously both entertaining and pissing everyone off at the same time.
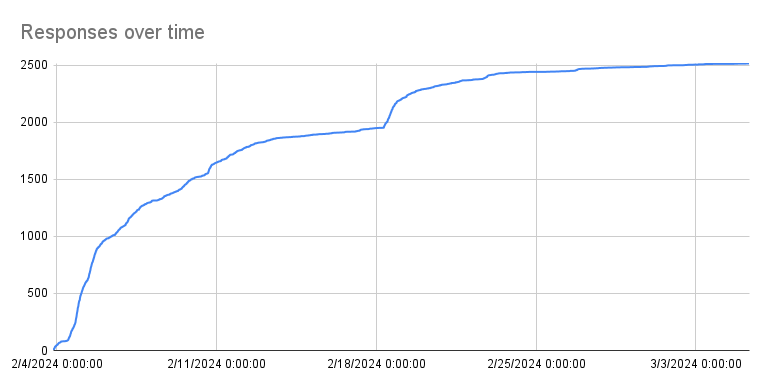
I never expected this to get so popular, and with the MCS now having over 2500 responses at the time of writing, I do feel some obligation to make good use of the data. I hope you find great joy and/or seething rage in looking through the results. If nothing else, I believe that the survey's results can help expose math enthusiasts around the world to popular mathematican notations or conventions that may be unknown to them. For example, numerous respondents were surprised that $0$ could be natural, or that there was any debate whatsoever on whether $f(x) = 1/x$ is continuous.
If you have about 5 minutes of spare time and energy, I'd highly recommend checking out the questions before seeing the results!
Some Credits:
This isn't really that important so you can just skip to results if you want.
Oh wow, you're still reading. I'm flattered.
Ok, here's some background. The survey opened up on February 3rd, 2024, 20:20:11 EST. The results on this page include all responses submitted up to March 5th, 2024, 8:33:24 EST, totalling exactly 2500 non-empty responses.

This project was supposed to be a joke, so I did not have high standards of scientific rigor in mind when conducting this survey. Nevertheless, there are a few semi-important kinks concerning the survey. First, there were actually two different copies of the survey sent out!
If you wrote down a university affiliation, or if I was able to confidently guess your university affiliation, then I marked you down as a university-affiliated respondent.
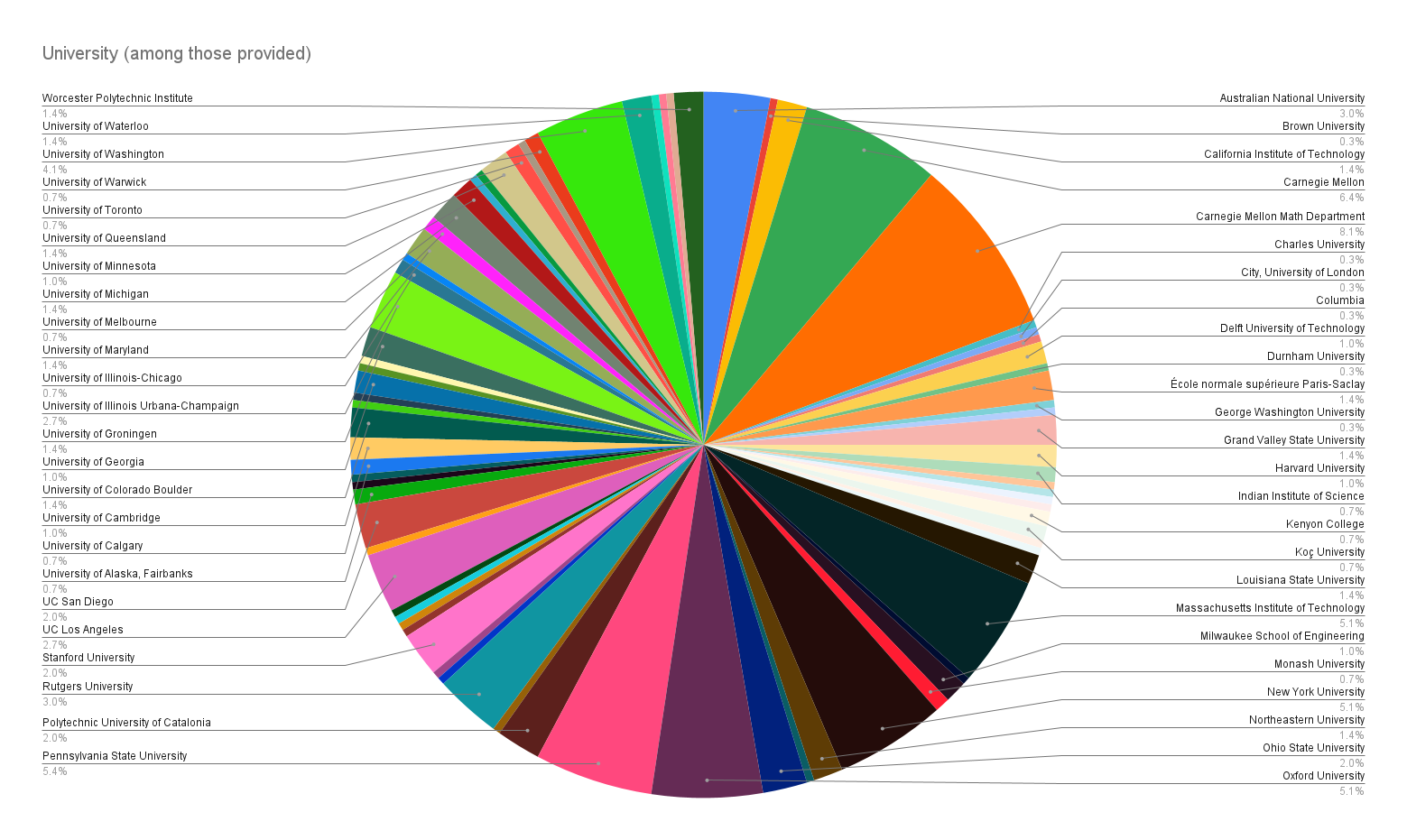
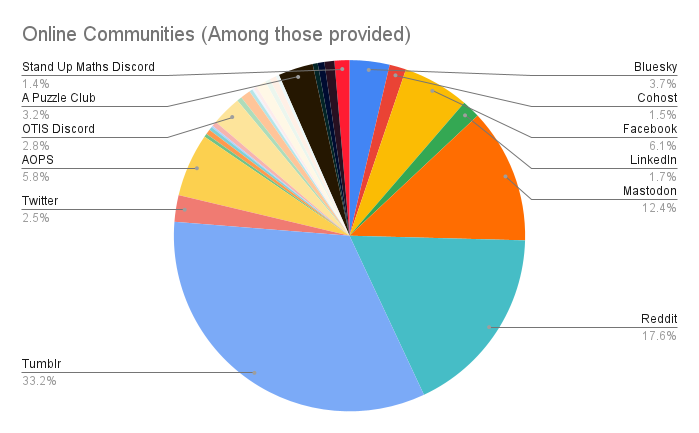
The above chart shows most of the universities. For the full list, please see the data sheet. Also included on the data sheet include a collection of some of the online communities and social media platforms that the survey reached.
A few more details and design decisions:
Possible sources of error include:
Without further ado, here are the results!
Navigation
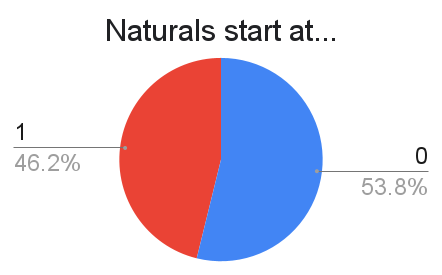
A slight majority for 0!
There was a notable difference between the surveys: In Form A, there were 24% more 0'ers than 1'ers, whereas in Form B there was a tie (!), with no significant difference. If we restrict to university-affiliated respondents, there were 72% more 0'ers than 1'ers, compared to only 13% among the other respondents. It's an interesting discrepancy!
This is the first and last time I'll mention any discrepancies between groups since it's gonna take more effort than I signed up for to repeat this analysis for every question. Most of the work is done for you in the data sheet though, so do check that out if you want to analyze the data yourself!

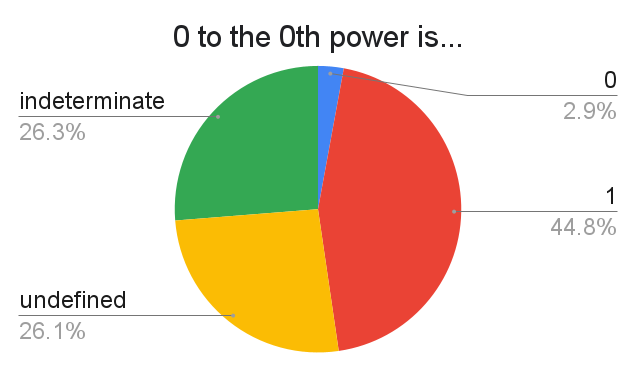
Chaos! A great $\approx 50\%$ majority adopts $0^0 = 1$, with "indeterminate" and "undefined" each taking about a quarter of the pie.
Interesting responses include:
The argument for $0^0 = 1$ is typically that adopting this value makes a bunch of formulas much nicer, especially in discrete settings. For example, it allows us to write the Binomial Theorem without worrying over $0$ as a special case.
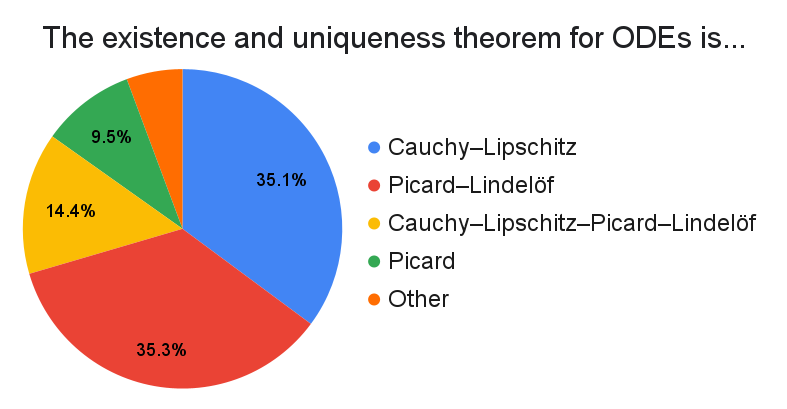
Those that say that $0^0$ is indeterminate are typically interpreting each "$0$" as a limiting value. That is to say, the information $\lim_{x \to x_0} f(x) = \lim_{x \to x_0} g(x) = 0$ is insufficient for determining $\lim_{x \to x_0} f(x)^{g(x)}$. To my knowledge, this is mostly discussed in Calculus courses.
As I understand it, the case for taking $0^0$ to be undefined is that there is no natural value for it in the realm of continuous mathematics. Indeed, I do not think there is a natural way to justify assigning a value to $0^0$ when constructing the real exponential. It could also be the case that $0^0$ is undefined because it corresponds to an indeterminate form.
I am not aware of any compelling argument for $0^0 = 0$.
Naturally, there is a Wikipedia on this issue: https://en.wikipedia.org/wiki/Zero_to_the_power_of_zero (Check out the talk page for some "entertainment"...)
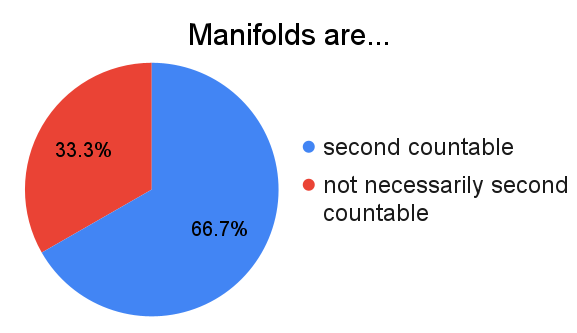
The rationale for second-countability is largely to ensure that manifolds are paracompact, which allows for the usage of useful tools such as partitions of unity. Requiring second-countability excludes objects such as the long line from being considered manifolds. As Topospaces puts it, "the long line fails to satisfy only the second condition for a manifold; it is simply too long."
One respondent commented that in their definition, manifolds are paracompact but not necessarily second-countable. As far as I'm aware, this doesn't really break much.
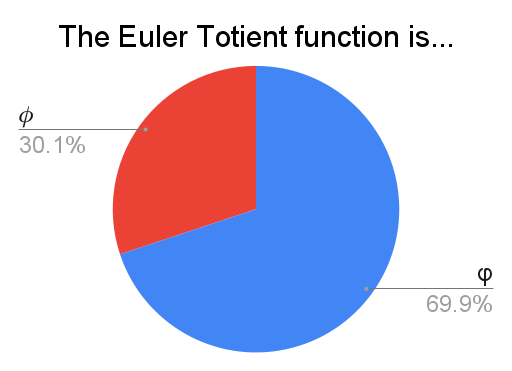
The curlier $\varphi$ wins over $\phi$ by a significant margin.
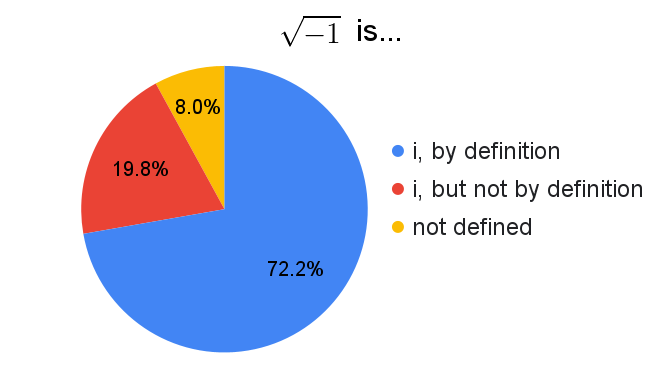
Unfortunately this question was potentially a bit vague. Let me explain the options and their intended meanings:
Other responses include:
I offer my insincere apologies to the engineers that would have preferred $j$.
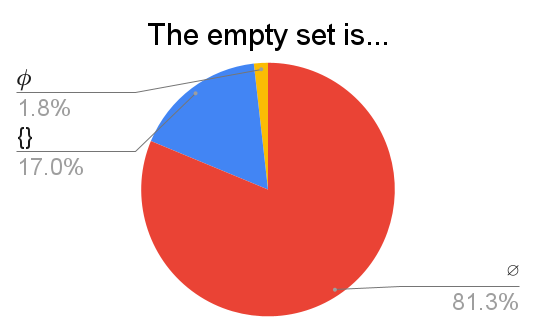
A few dozen respondents were fine with either $\{\}$ or $\emptyset$. I am aware that $\emptyset$ and $\varnothing$ are distinct, and it's unfortunate that this slipped my mind. Unicode can't tell the difference between them, so let's consider them the same for this question.
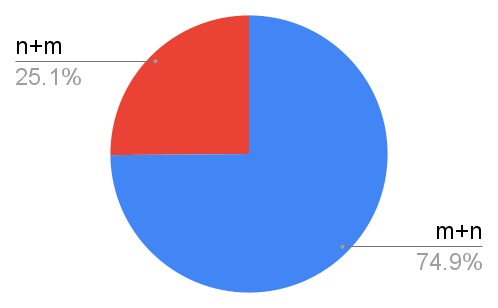
After years of writing $n+m$, my reality was shattered when I realized that $n$ does not, in fact, come before $m$ in the alphabet.
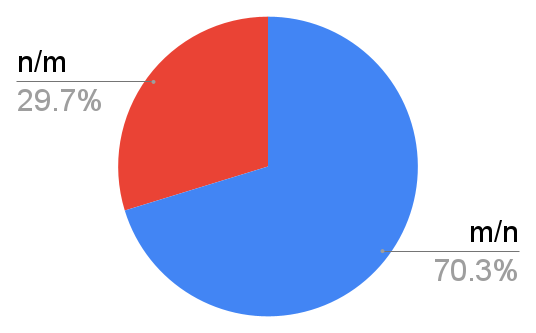
The previous two charts differ slightly. Naturally this demands further analysis. Here's a chart of how people responded to both questions, among all those respondents that answered both questions.
$N = 2271$
| $m/n$ | $n/m$ | |
| $m+n$ | 64% (1456) | 11% (247) |
| $n+m$ | 6% (141) | 19% (427) |
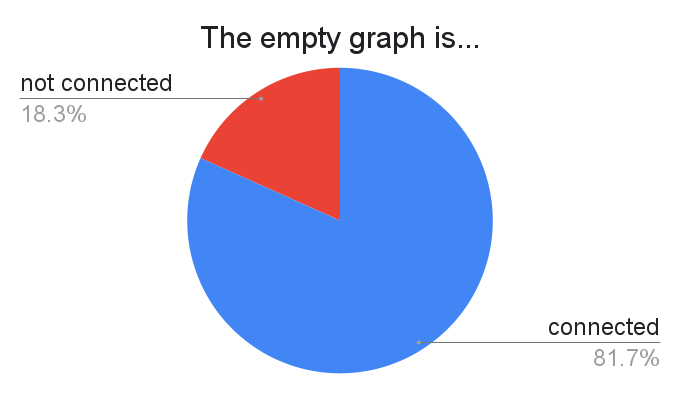
This question can be the subject of very long arguments. At first glance, it may be obvious that the empty graph is connected because it is vacuously true that any pair of points in the empty graph can be connected by a path. But there are also rather compelling arguments for adopting the convention that the empty graph is not connected! Some of these include:
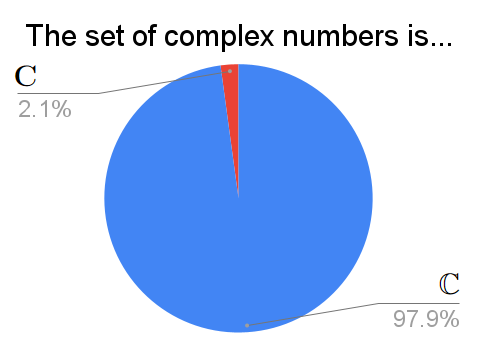
A largely unsurprisingly result, and there were no significantly common write-ins.
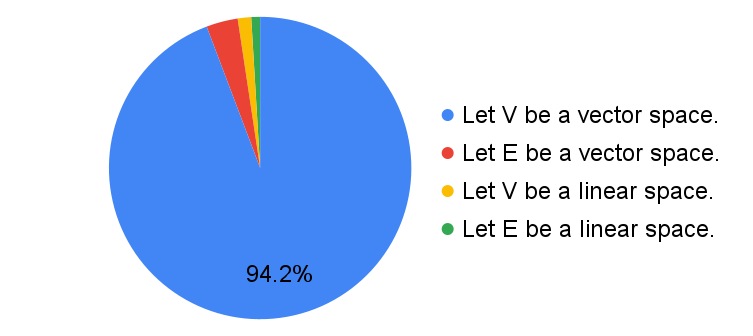
According to Wolfram MathWorld, the term "linear space" is most commonly seen in functional analysis. The preference of $E$ over $V$ for vector spaces is also prominent in this field, from what I can tell. (See e.g. Functional Analysis, Sobolev Spaces, and Partial Differential Equations by H. Brezis.)
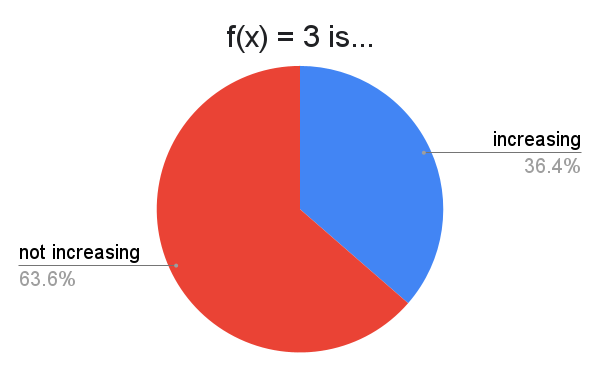
Proponents of "increasing" are using the definition that a function $f$ is increasing if $f(x) \leq f(y)$ whenever $x \lt y$. If instead $f(x) \lt f(y)$ for all such $x,y$, then $f$ is "strictly increasing".
Those who instead take the latter $f(x) \lt f(y)$ definition to mean "increasing" may characterize the former $f(x) \leq f(y)$ definition as "non-decreasing".

The bra-ket notation $\langle v | w\rangle$ was very prominent in the write-in responses, so it is included in the chart. Other responses include:
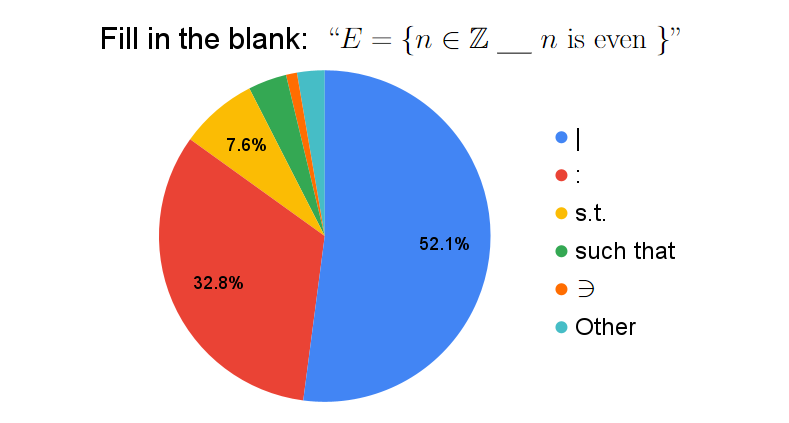
I got a few comments preferring notation such as $E = \{n | n \in \mathbb{Z}, \text{$n$ is even}\}$. Common write-ins include indecision between $|$ and $:$, and fierce hatred towards $|$.
As jarring as it may be, $\ni$ is apparently a real symbol used by real people.
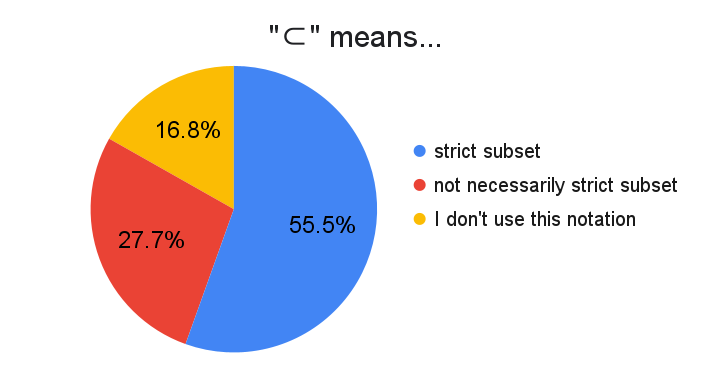
This data sugests that we may want to avoid writing $\subset$ if the difference between "subset" and "strict subset" is important. To dodge the ambiguity of $\subset$, I believe it is common to write $\subsetneq$ or $\subsetneqq$ to denote a strict subset.
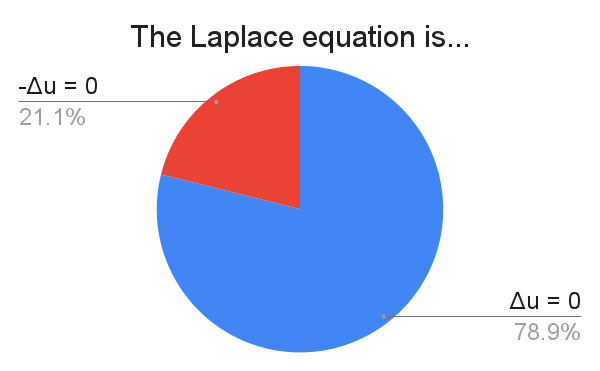
The rationale for $-\Delta u = 0$ is that $-\Delta$ is somehow a more "natural" operator than $\Delta$. In particular, integration by parts shows that $\int_\Omega F \cdot \nabla u\,dx = \int_\Omega (-\operatorname{div} F)u\,dx$ for $u,F$ compactly supported, so the adjoint of the gradient operator is $\nabla^* = -\operatorname{div}$, and now $\nabla^*\nabla = -\operatorname{div}\nabla = -\Delta$. Also, $u$ is subharmonic iff $\Delta u \geq 0$, which is easier to remember as $-\Delta u \leq 0$.
I received at least one comment that takes this philosophy to the extreme, defining $\Delta$ to be $-\operatorname{div}\nabla$. Several respondents would have liked to see $\nabla^2$ instead of $\Delta$.
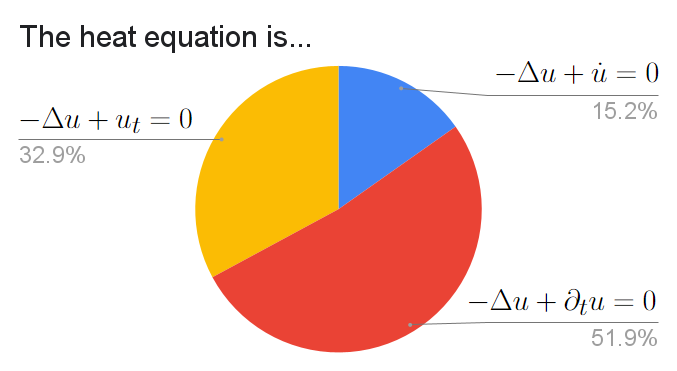
This was just a matter of how you denote time derivatives in PDEs. It would appear that $\partial_tu$ is the majority favorite, with the "dot" notation losing favor.
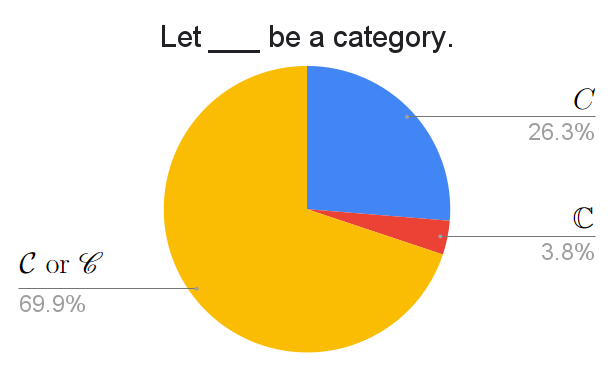
My category theory professor should steer clear of Respondent #859.
Mathematical philosophy is fun! But I am absolutely not an authority in the field, so I'll instead direct you to the Stanford Encyclopedia of Philosophy. See e.g. Platonism and Fictionalism.
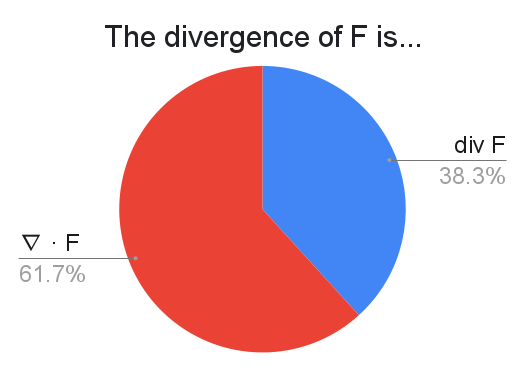
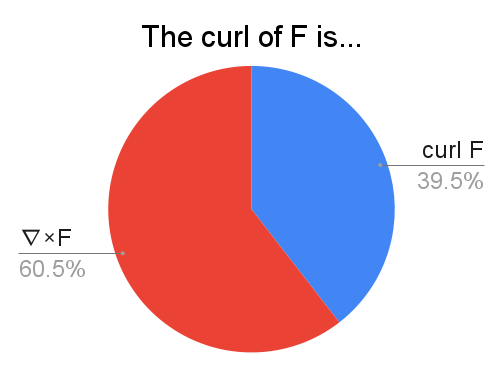
It's time for another table! How many people chose each possible combination for denoting divergence and curl?
$N = 1815$
| $\operatorname{curl} F$ | $\nabla \times F$ | |
| $\operatorname{div} F$ | 35% (642) | 3% (51) |
| $\nabla \cdot F$ | 4% (73) | 58% (1049) |

$(+,+,+)$ was not an option since it's hard to imagine how it could be anything other than the 1st octant. Anyways, here are two alternative visualizations of the data, depending on whether you think up is $y$ or $z$.
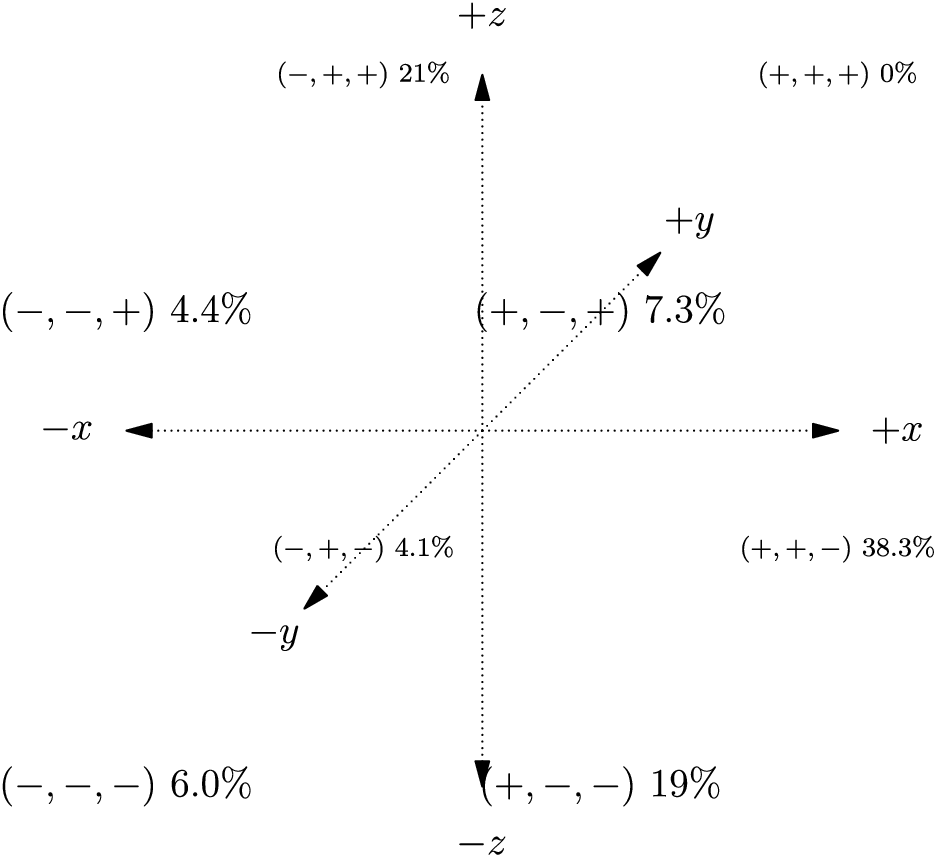
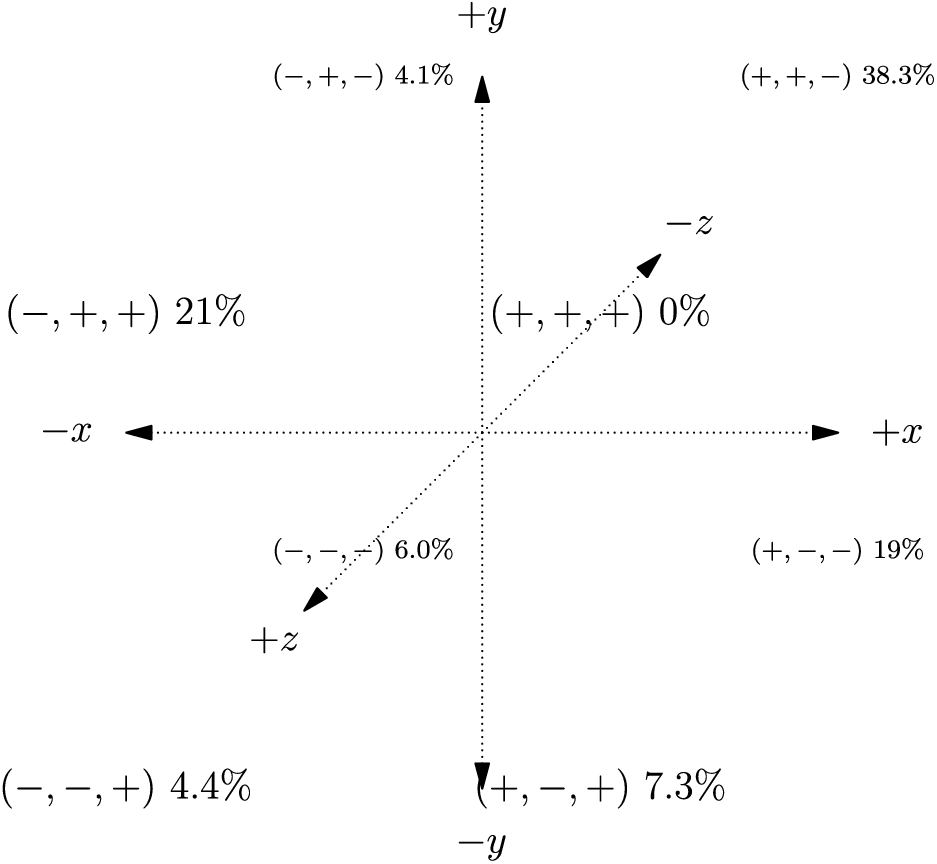

Many respondents were indecisive.
Several respondents stated that $\mathbb{Z}_p$ should be the "localization of the integers at $p$". I don't know what that means and I'm too afraid to ask.
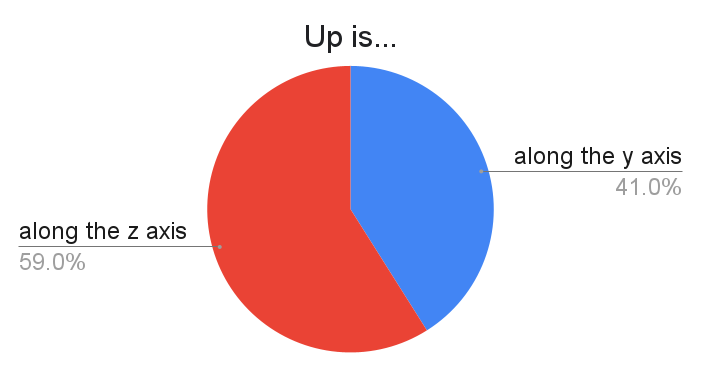
The axes should comply with the right-hand rule, but besides that, there seem to be a bunch of different ways that people like to orient the axes. Having "up" be the positive $y$-axis is quite common in 3D videogames, with the view that "the third axis ($z$) adds depth to the 'right/up' plane". Having "up" be the positive $z$-axis is from the view that "the third axis adds height to the flat horizontal/vertical plane".
Apparently, some people that fly airplanes take "up" to be the negative $z$-axis.
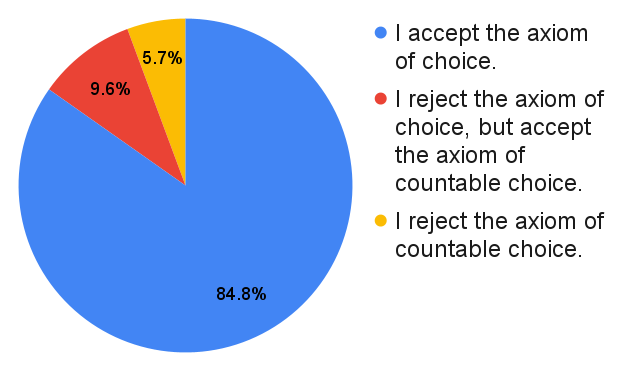
Several angry set theorists have remarked that I should have put down "dependent choice" instead of "countable choice". Whoops.
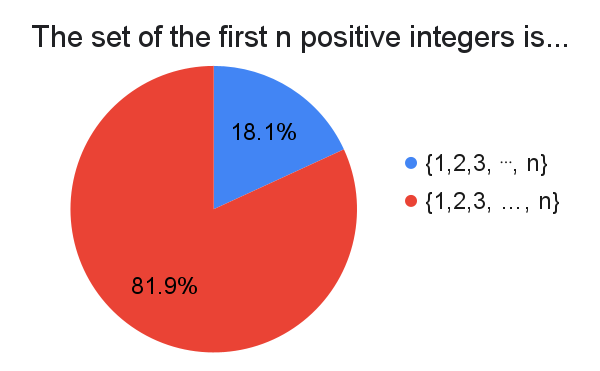
This question was about where you like to align the dots. Should they be centered ($\cdots$) or lowered ($\ldots$)? The overwhelming consensus appears to be lowered.
A number of respondents complained that neither answer was correct because $0$ is positive. I forgot that people do that.

Once again, the curlier option is superior!
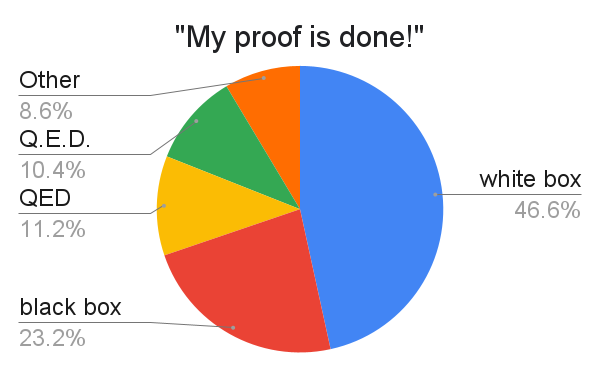
Total chaos! The "Other" responses include:
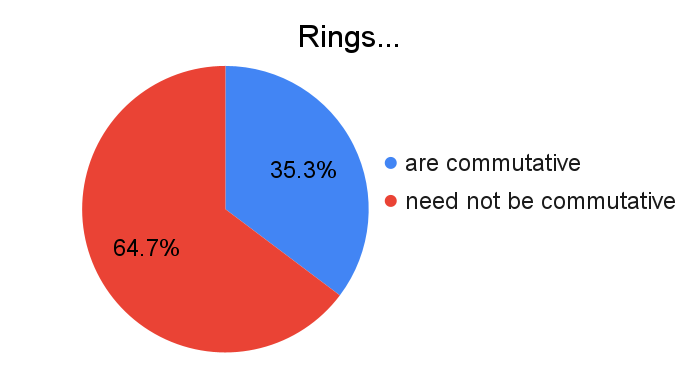
The majority rules that rings do not necessarily satisfy $ab=ba$ for all elements $a$ and $b$...
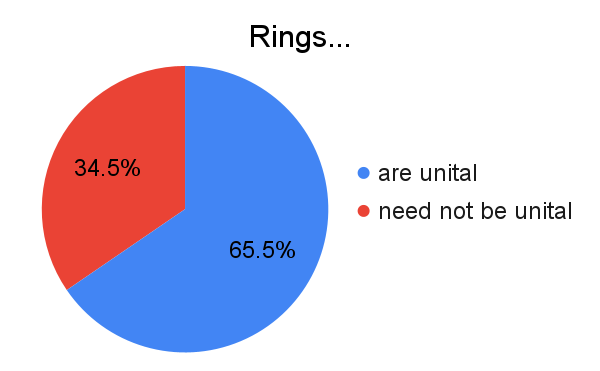
...but are assumed to have an identity element.
Chart time!
$N = 1515$
| Rings are... | unital | not necessarily unital |
| commutative | 27% (406) | 7% (101) |
| not necessarily commutative | 38% (580) | 28% (428) |
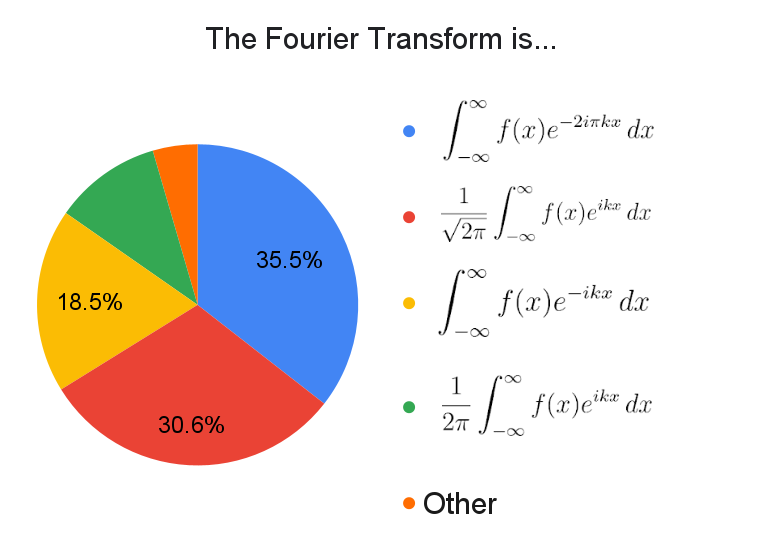
I pulled these four options from the Mathematica documentation for the Fourier Transform (See "Details and Options", where the page explains FourierParameters). But there are still a bunch of different variants not listed.
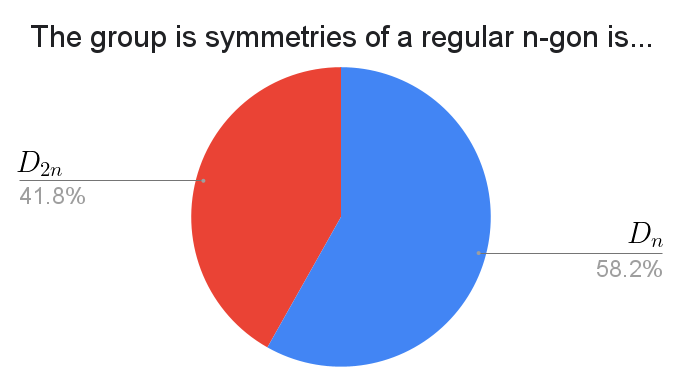
The rationale for $D_n$ is that $n$ is just the number of sides, whereas the rationale for $D_{2n}$ is that the number of elements in the group is $2n$.
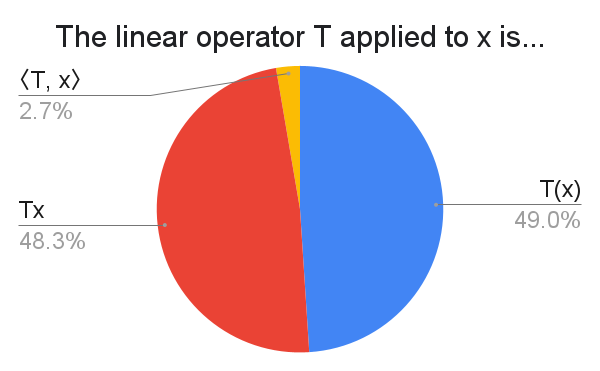
The possibly jarring $\langle T, x\rangle$ notation is seen in functional analysis. It's interesting to see the "rebellious" $Tx$ being so evenly matched with $T(x)$.

Some have no such mnemonic, since this is country-dependent. I believe PEMDAS is US-centric whereas BODMAS is used at least in the UK and India.
Apparently there are numerous other mnemonics. The write-ins include:
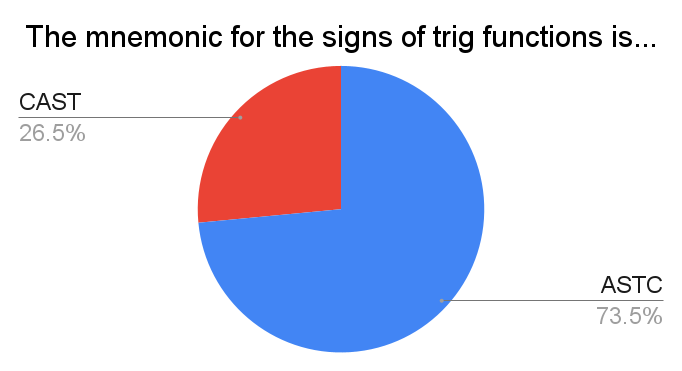
This is again quite country-dependent, and in particular such trigonometric mnemonics are probably heavily US-centric.
The idea is that these letters, when placed on the four quadrants of the unit circle, outline which of the three trig functions $\sin(x),\cos(x),\tan(x)$ are positive on each quadrant. For instance, the second letter of ASTC is S, indicating that on the second quadrant $\pi/2 \lt x \lt \pi$, only $\sin(x)$ is positive. "ASTC" is memorized with funny phrases such as "All Students Take Calculus" or "All Students Try Cheating". Though, I sense that the latter may be in bad taste...
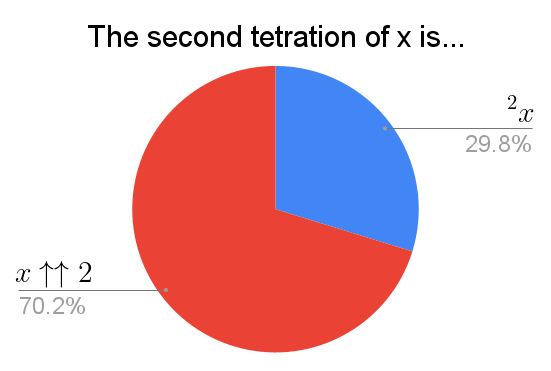
"Up-arrow" notation wins!
The $n$th tetration of $x$ is essentially the value of the "power tower" formed by $n$ $x$'s. So the second tetration of $x$ is just $x^x$. Wikipedia lists some other notations for tetration.
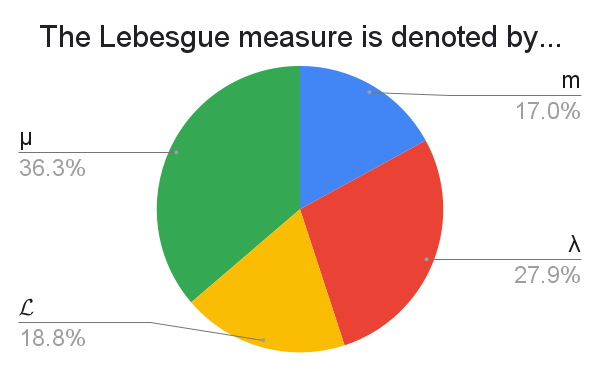
$\mu$ seems to have the edge, but there is no clear consensus. Write-ins include:
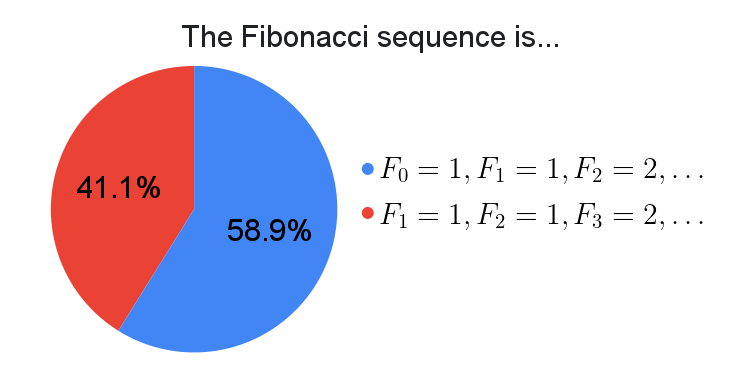
A dozen or so respondents complained that the second option should have a zeroeth term, $F_0 = 0$. They have a good point, my bad.
A nice thing to note about the second option $F_1=1,F_2=1,F_3=2,\ldots$ is that it gives the aesthetic identity $\gcd(F_m,F_n) = F_{\gcd(m,n)}$. This property is also consistent with $F_0 = 0$.
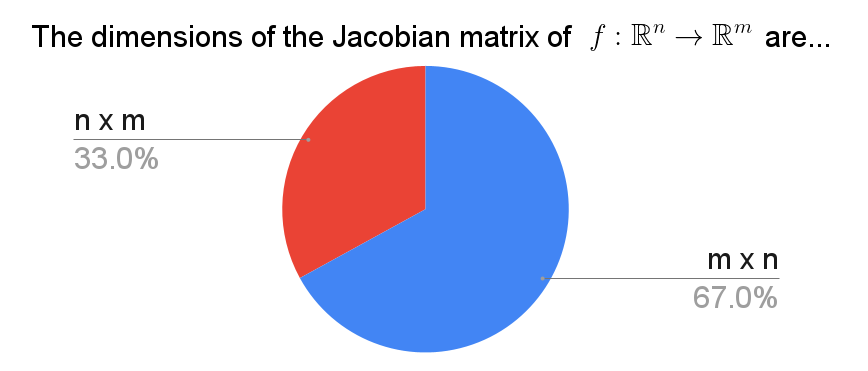
I am not familiar for reasons to take the Jacobian to be $n \times m$.
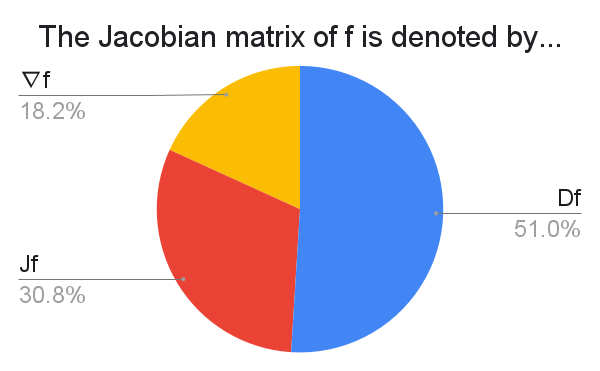
Other responses include:
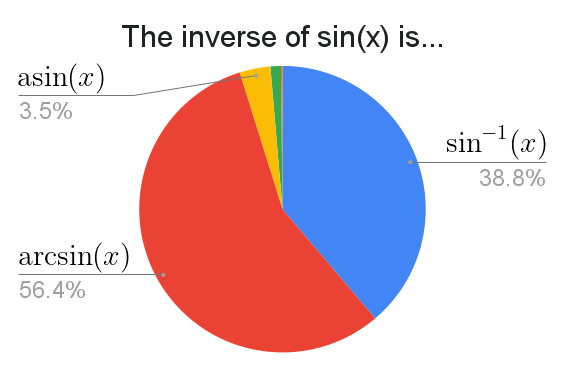
The unpopular, unlabeled slices of the pie are $\operatorname{Arcsin}(x)$ (in green) and $\operatorname{Asin}(x)$ (in orange).
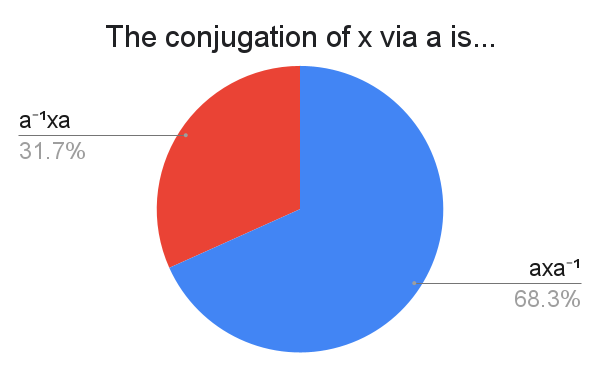
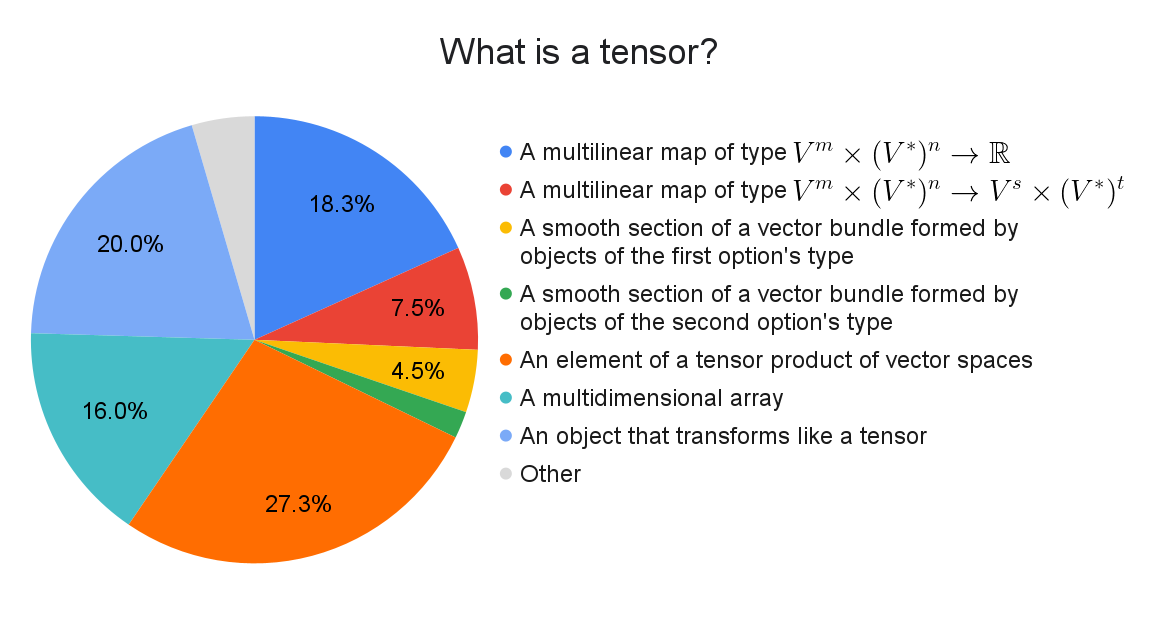
This survey has confirmed what we all knew: nobody actually knows what a tensor is.
Other responses include:
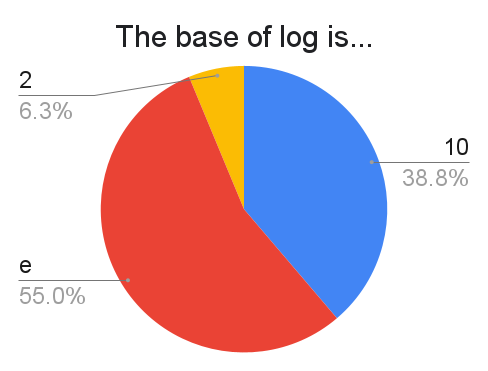
Taking the base to be $e$ becomes more prevelant upon pursuing a math degree. Taking the base to be $2$ is favored by some computer scientists.
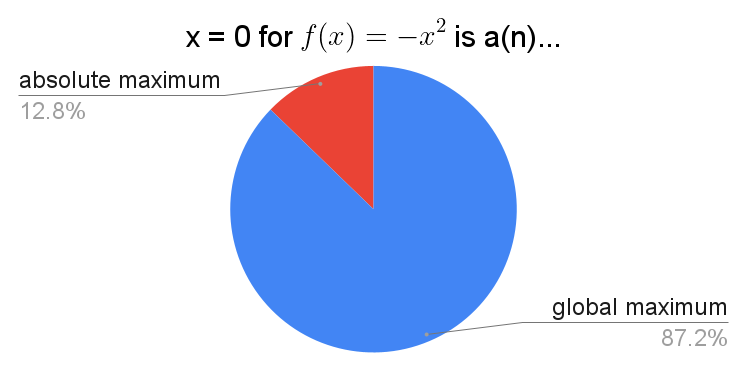
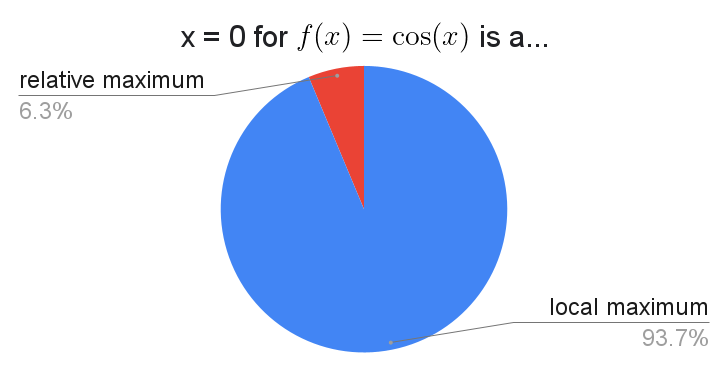
Time for another chart!
$N = 2117$
| local | relative | |
| global | 85% (1800) | 2% (50) |
| absolute | 9% (186) | 4% (81) |
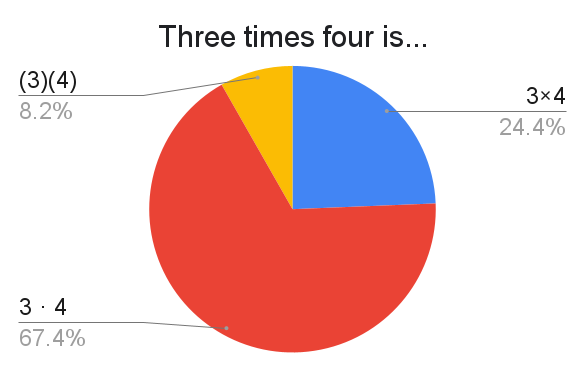
There were several respondents that preferred $3(4)$ over $(3)(4)$. That probably would've been a good option.
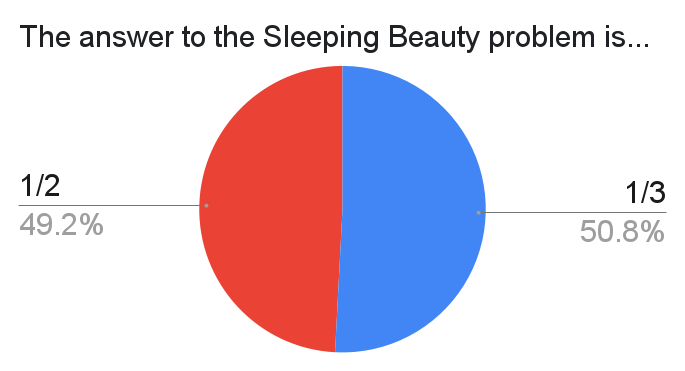
For those unfamiliar, see Wikipedia. It's quite the conundrum! The survey confirms that the problem's answer is highly contested with pretty much no consensus.
A dozen or so respondents say that the problem is not well-defined.
The question was worded slightly differently in the survey ("In the Sleeping Beauty problem, what is the probability that the coin flipped heads?"), causing a few respondents to harp on the lack of conditioning on the event of being woken up. I think that's a bit pedantic --- the intent of the question should be obvious.
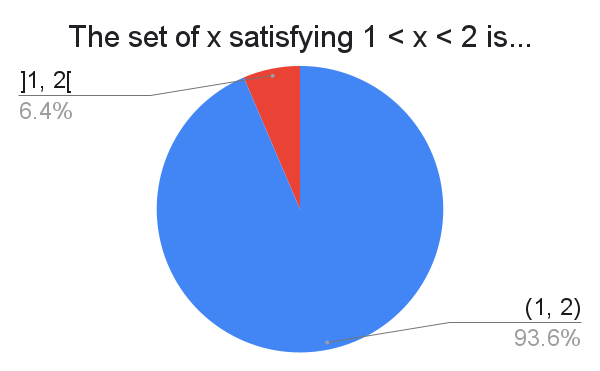
For those that are mortified at "$]1,2[$", I believe this is a convention that is seen in France (and maybe other countries?).
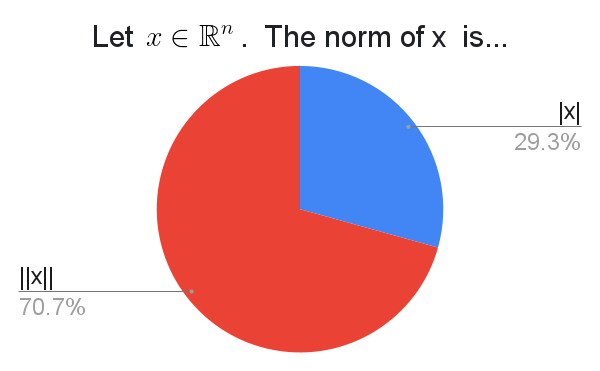
While $\|\cdot\|$ is the standard notation for a norm, it is not uncommon to write the "shortcut" $|\cdot|$ when in Euclidean space.
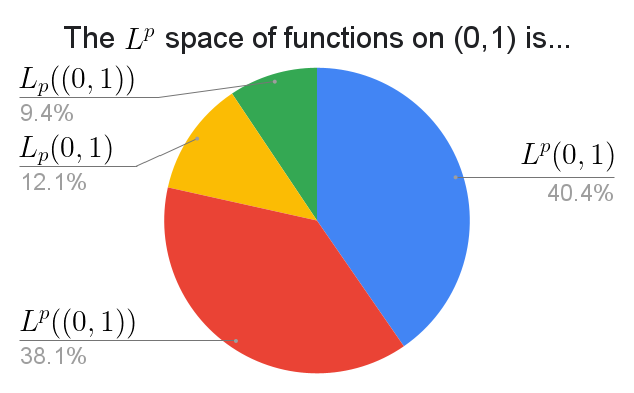
This was a question about two different conventions:
There were some write-ins, but they varied quite a bit.
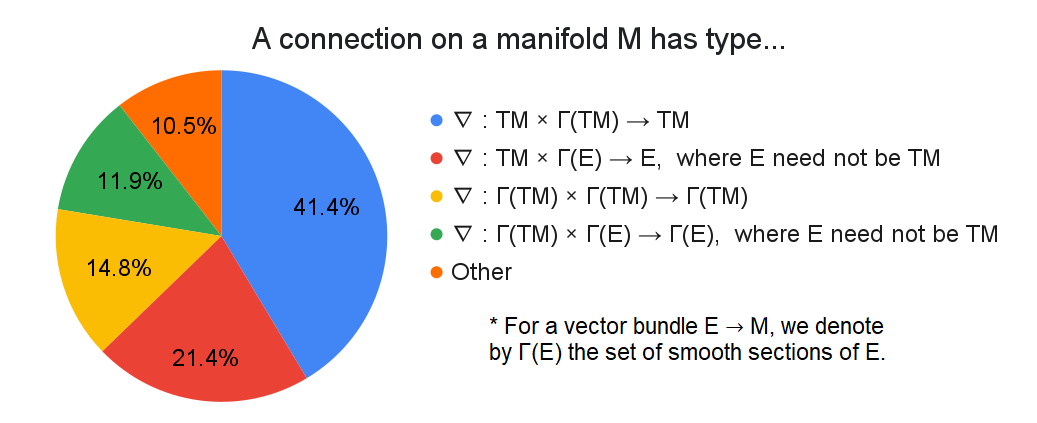
I included this question for purely selfish reasons. I struggled for an eternity last semester trying to understand what a connection is since there was seemingly a ton of conflicting definitions. One reason for this is because there are like a billion different types of connections. At least as it pertains to smooth manifolds, a general sort of connection is this thing, which can be used on vector bundles other than the tangent bundle. Then there's the affine connection, where the $X$ and $Y$ in $\nabla_XY$ both need to be vector fields. Then there's the covariant derivative which I'm pretty sure is just the same bloody thing as an affine connection except in "local form". Speaking of which, you can define a connection in either a "global" or "local" sense (see here). AAAAAAAAAAAAAAAA.
Anyways, figuring this out was painful and I wanted to know if there was any consensus. It would appear that the "local form" for the affine connection, or perhaps the "covariant derivative", with type $\nabla:TM \times \Gamma(TM) \to TM$, is the clear winner. Yay!
Other resposnes include:
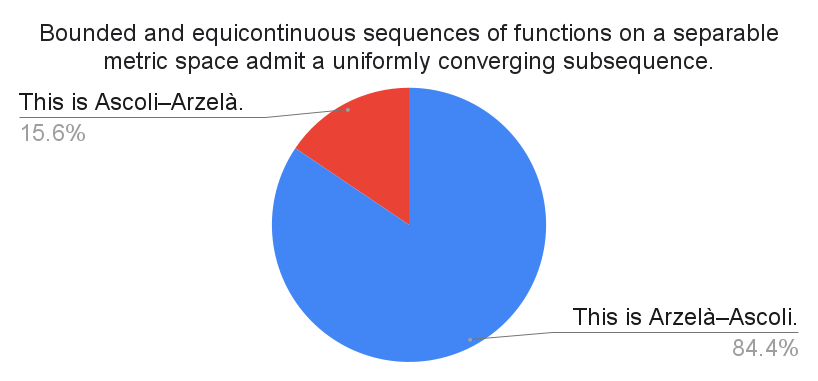
My Italian advisor has always written "Ascoli–Arzelà" and I refuse to change.
Other languages that put Ascoli before Arzelà include Ukrainian, Japanese, and Russian. Interestingly, the French exclude Arzelà's name from the theorem, whereas Kazakhstan excludes Ascoli.
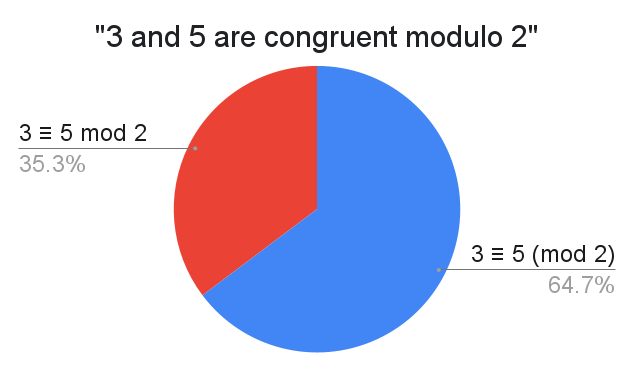
Among the write-ins, variants in where the "2" is placed include:
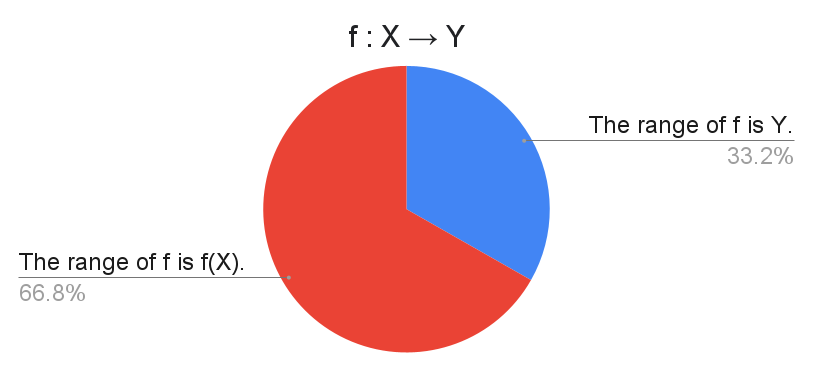
Both definitions for the range are widely taught. Neither option seems necessarily superior: If the range is $f(X)$, then $Y$ can be called the codomain, and if the range is $Y$, then $f(X)$ can be called the image.
In the current century, defining the range to be $f(X)$ is said to be more popular, as the survey shows. It also makes the name of the Closed range theorem sensible. It's certainly not an overwhelming majority though, so it should be good practice to clarify the meaning of "range" if we ever choose to use the term.
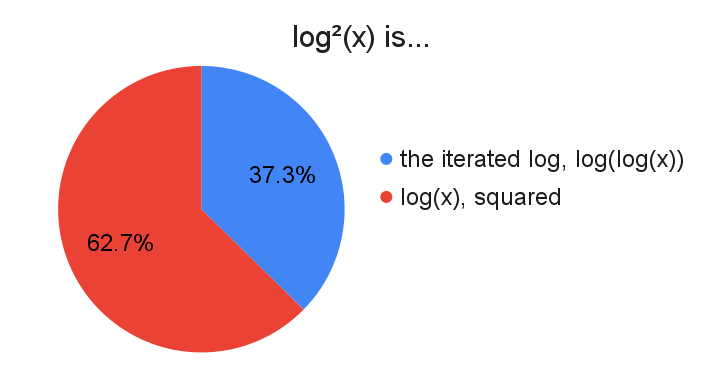
Ambiguous superscripts bring endless joy.
You've made it more than halfway! Here's a joke: What do mathematicians burn in their fireplaces?
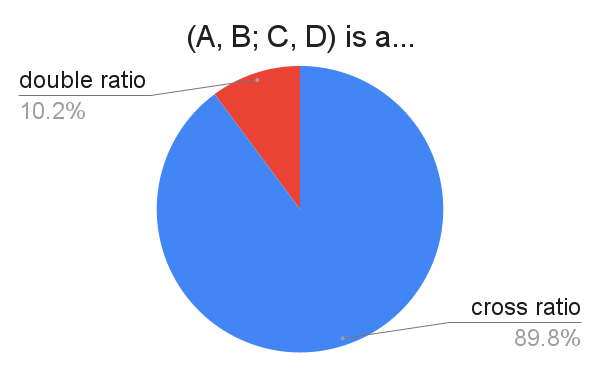
This is a fundamental quantity in projective geometry. Essentially, when $A$, $B$, $C$, and $D$ are on the same line in 3D space, then the value of $\frac{CA}{CB} \div \frac{DA}{DB}$ stays the same no matter where you "view" the points, which lets you compute some lengths in photographs. I recall this technique being helpful in tracking down Osama bin Laden, but I'm unable to procure a source for this.
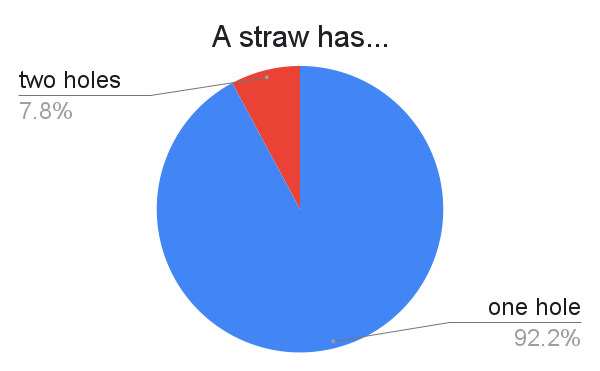
This is a popular controversial question. At last, we have the authoritative mathematical consensus: A straw has one hole!
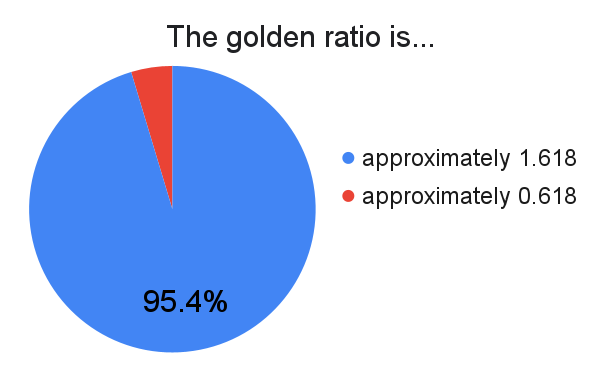
Namely, is it $\frac{1+\sqrt{5}}{2} \approx 1.618$ or $\frac{\sqrt{5}-1}{2} \approx 0.618$? The question may seem pointlessly obvious, but it was inspired by a news story about a decade ago which was caused by differences in the exact definition of the golden ratio. See here for a news article. Essentially, the fuss is that both $\frac{1+\sqrt{5}}{2}$ and $\frac{\sqrt{5}-1}{2}$ have the same idea, being reciprocals of each other. It's just a matter of whether you want the bigger number in the numerator or the denominator.
Well, we've now confirmed that $\varphi = \frac{1+\sqrt{5}}{2}$ is the overwhelming consensus.
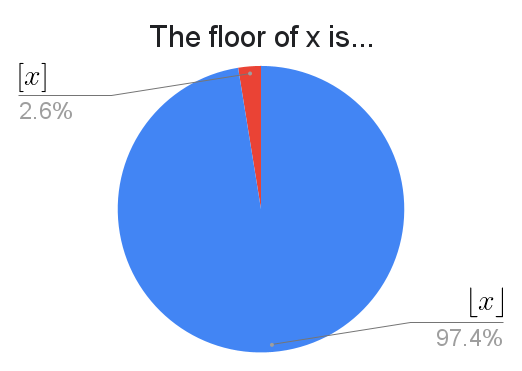
My current probability professor writes $[x]$. It exists. Fear it.
I wonder what $[x]$ users write for the ceiling?
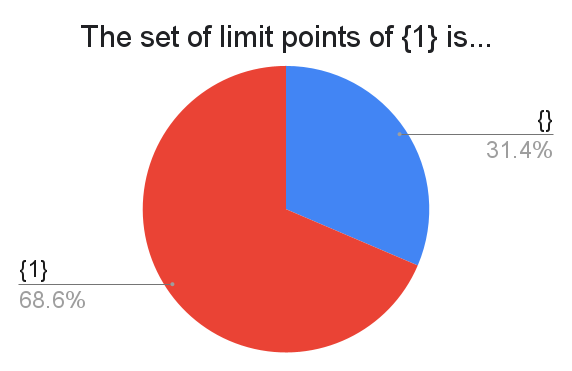
The definition of a limit point is not universally agreed upon (though I admit that I had to do some digging for that link). The less ambiguous terms in question are accumulation point (every neighborhood of $x$ has a point in the set different from $x$) and adherent point (every neighborhood of $x$ has a point in the set, and it could be $x$). So does "limit point" mean accumulation point or adherent point? If you thought "accumulation point", then you chose $\{\}$. If you thought "adherent point", then you chose $\{1\}$.
It appears that a decent majority chose $\{1\}$, allowing to take the point itself in the definition of a limit point, which disagrees with Wikipedia, Wolfram Mathworld, Proof Wiki, and many MSE posts. Fascinating.
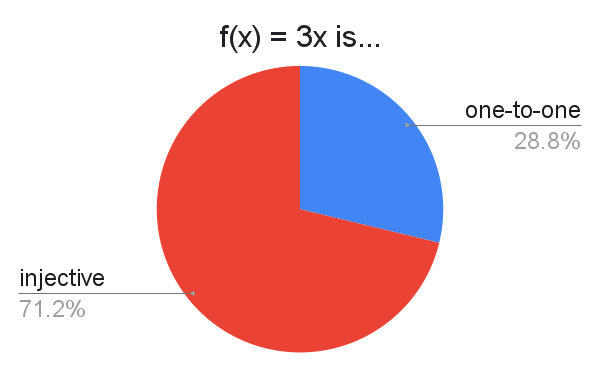
Every time someone says "one-to-one", I cry a little.
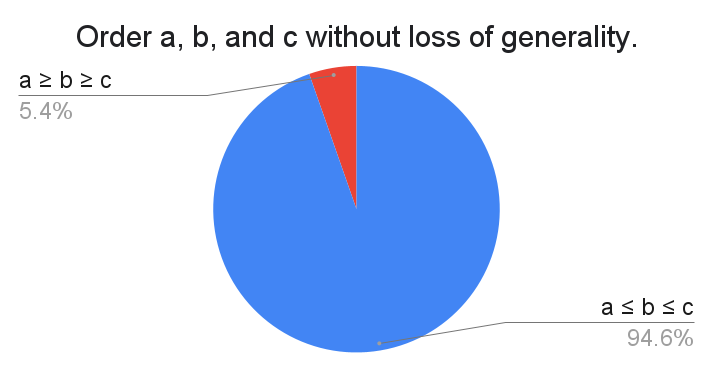
Essentially, suppose you have a question like "Prove that $\frac{a+b+c}{3} \geq \sqrt[3]{abc}$ for all $a,b,c \geq 0$", where the roles of each of the variables $a$, $b$, and $c$ are symmetric. Then you can assume some order on them. Is it aesthetically preferable to assume $a \leq b \leq c$ or $a \geq b \geq c$? A very strong majority has chosen the former.
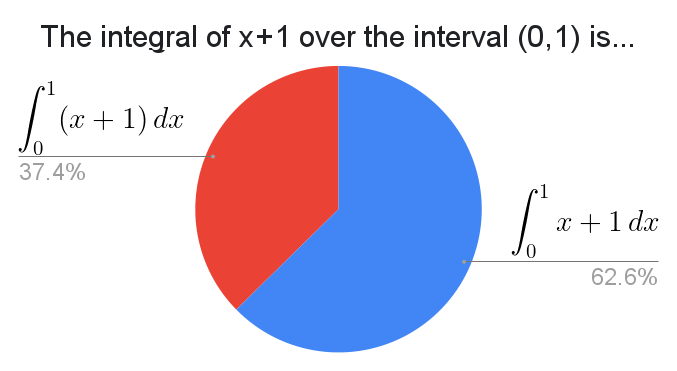
A number of physicists wanted to have $dx$ before the integrand, as in $\int_0^1 dx\,(x+1)$, but for this question I only cared about whether or not you enclose the integrand in brackets when the integrand has multiple terms.
I believe the rationale behind brackets is that the integrand is being multiplied by the differential, so writing $\int_0^1 x+1\,dx$ wouldn't mean what you want it to mean because the order of operations dictates that the product $1\,dx$ happens before you add $x$. But it would appear that a majority either don't care or don't think that way.
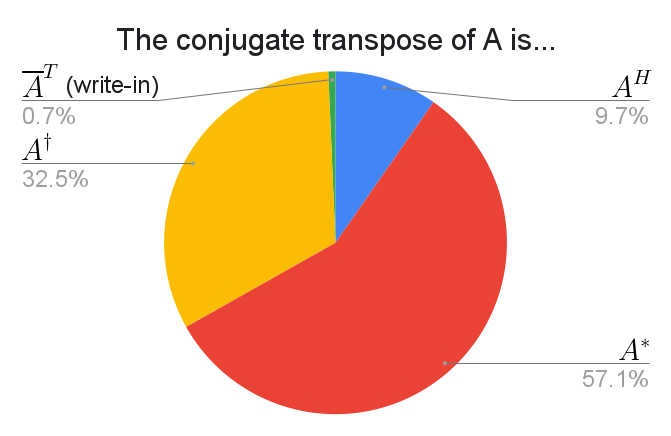
$A^\dagger$ was not originally among the default choices, which was quite clearly a major blunder on my part.
The $H$ in $A^H$ stands for Hermitian, which is a synonym for the conjugate transpose.
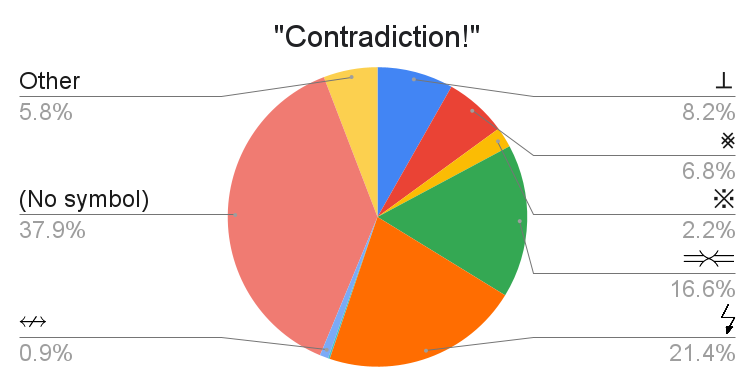
Most do not have a symbol, with the lightning bold and the "clashing implication arrows" being popular options among those that use a symbol. Other responses include:
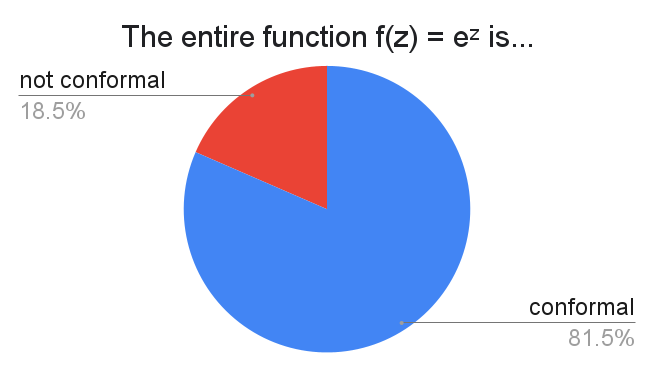
The clash here stems from the fact that there are two non-equivalent definitions of a conformal map. Most commonly (as suggested by the survey), a holomorphic $f:U \to \mathbb{C}$ is said to be conformal if its derivative $f'(z)$ never vanishes. In this case, $e^z$ is conformal. However, some say that $f$ is conformal if it is holomorphic and injective. This is a stronger property due to complex analysis shenanigans, and under this definition $e^z$ is not conformal because it is not injective.
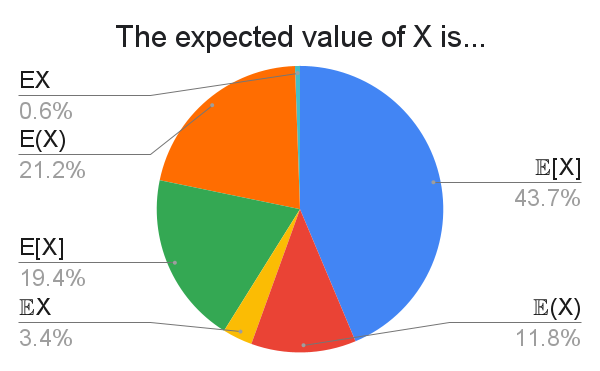
It's interesting to see $E(X)$ and $E[X]$ both being more popular than $\mathbb{E}(X)$.
Other responses include:
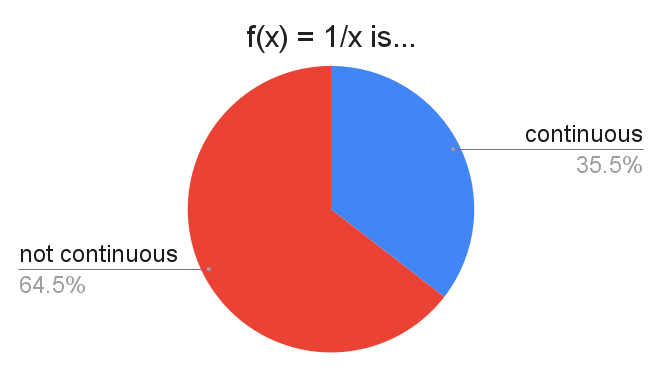
Many people are understandably flabbergasted that there is any debate here. $\frac1x$ obviously "jumps" at $0$. How could it be continuous?
The motto for the "$\frac1x$ is continuous" camp is "since $0$ isn't in the domain, it can't cause issues for continuity". Indeed, the standard definition for a function $f$ being continuous is that $f$ is continuous at every point in its domain, and this cannot be denied for $f(x) = 1/x$.
In certain parts of math, you might not consider $1/x$ to be continuous because $\{0\}$ is a null set, so $1/x$ is essentially a function $\mathbb{R} \to \mathbb{R}$ with no continuous representative.
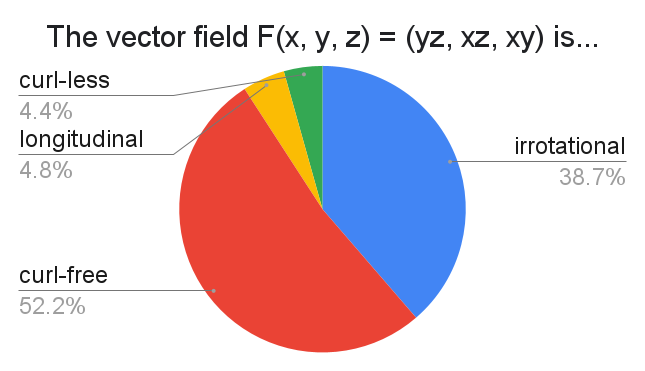
The popularity of "irrotational" is not too far off from that of "curl-free"!
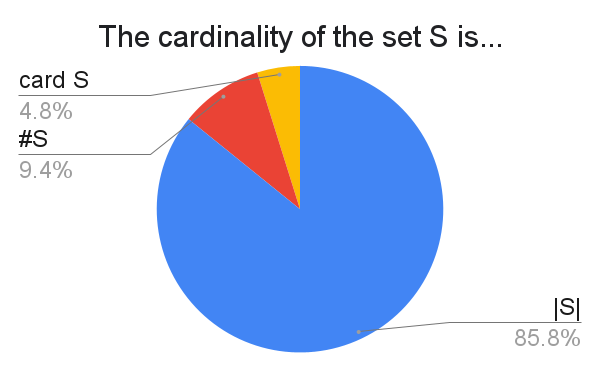
Some respondents said they use different notations depending on context. The write-ins were otherwise not very noteworthy.
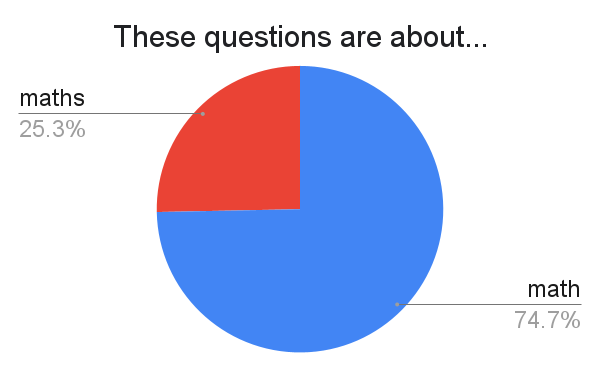
"How American are you?"
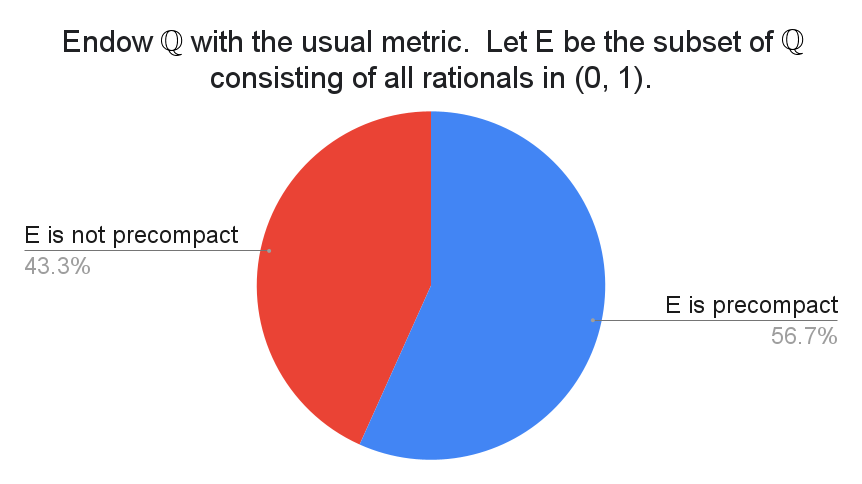
Intuitively, precompctness is the property of being well-approximated by finite sets. Unfortunately, "precompactness" refers to two different definitions.
Precompactness could mean relatively compact, meaning that the closure is compact. The closure of $E$ is $\mathbb{Q} \cap [0,1]$, which is not compact because given an enumeration $\{q_n\}_n$ of $\mathbb{Q} \cap [0,1]$ we may construct the open cover $\bigcup_{n=1}^\infty \left(q_n - \frac{1}{100^n}, q_n+\frac{1}{100^n}\right)$ which has no finite subcover. So $E$ is not precompact under this definition. It is important to note that the closure is not $[0,1]$ because the ambient metric space is $\mathbb{Q}$.
Precompactness could also mean totally bounded, meaning that for every $\varepsilon > 0$ there exist a finite number of balls of radius $\varepsilon$ that cover the set. It is not hard to show that $E$ is totally bounded, so $E$ is precompact under this definition.
The survey suggests that there is no clear consensus on what "precompact" means. Fortunately, the two definitions are equivalent in any complete metric space. So, for instance, Ascoli–Arzelà can be phrased in terms of precompactness without any ambiguity.
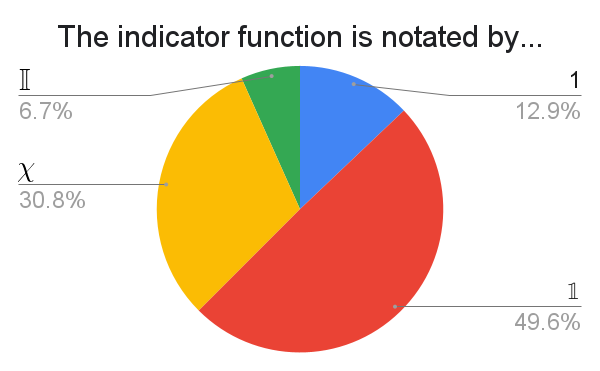
Standards may differ depending on exactly which field of math you're using indicator functions in. $\chi$ stands for "characteristic", and the other three notations have clear motivations. Other responses include:
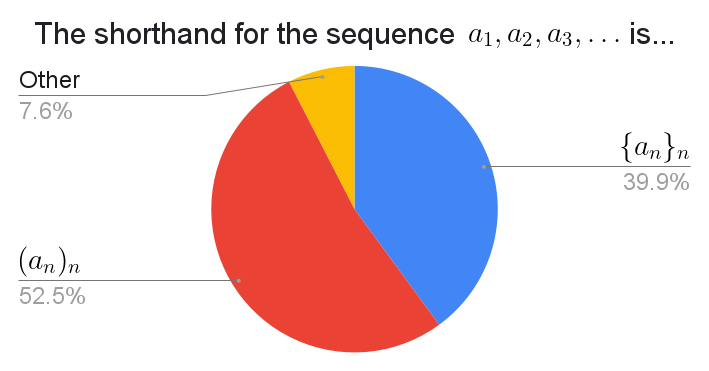
The write-ins were total chaos. Many respondents expressed a preference for multiple options, and if so then I assigned $0.5$ for every such choice, even if there were more than two. I combined different forms if they were essentially the same. With all that in mind, the top "Other" choices include:
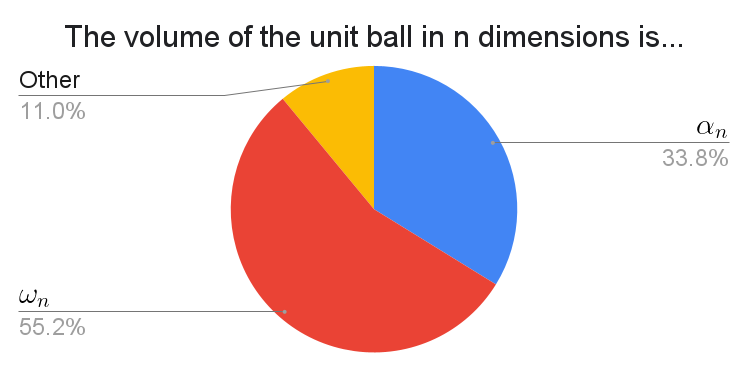
Among the write-ins, a few suggested "$V_n$", but most said they had no notation for this.
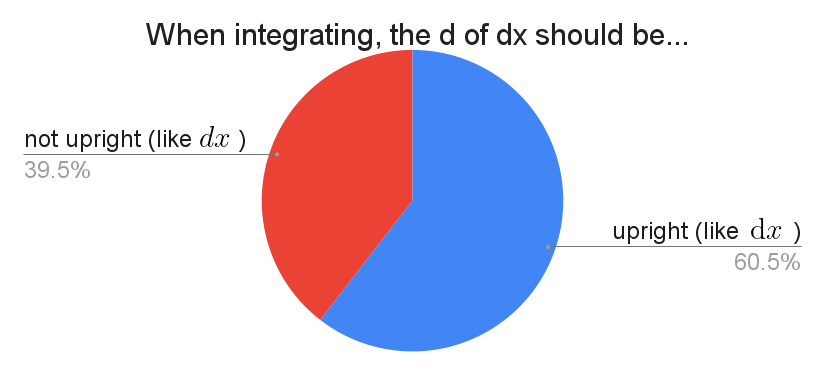
Someone should make a follow-up survey about how much space is included between the integrand and $dx$.
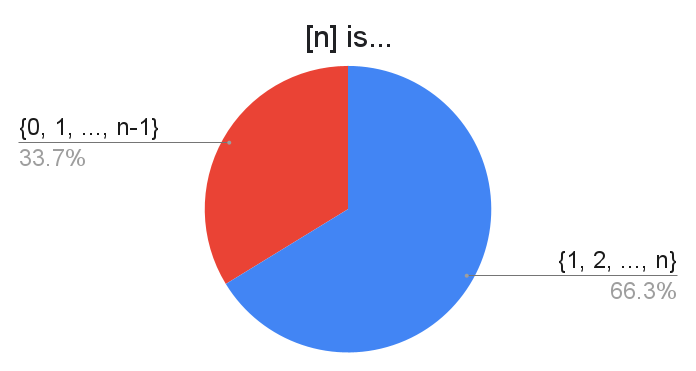
A popular complaint was the lack of the option $\{0,1,\ldots,n\}$. The motivation for this comes from the study of simplices, perhaps in algebraic topology. In the simplex category, $[n]$ refers to the object corresponding to the totally-ordered set $\{0,1,\ldots,n\}$. See also simplicial set. At a basic level, I believe the idea is that you want to be able to label the vertices of an $n$-simplex with the set $[n]$. For example, a 3-simplex is a tetredron with 4 vertices, which we can label as $0,1,2,3$.
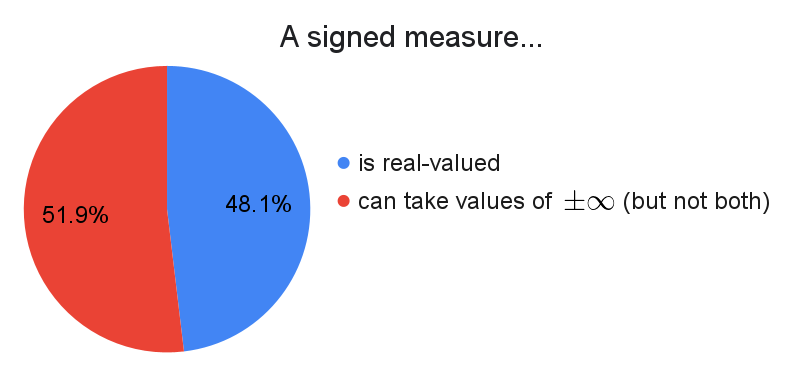
If we allow a signed measure $\mu$ to take values $\pm\infty$, then it can only take on one of them, otherwise there will be a set with measure $+\infty-\infty$, which is quite bad.
As per the survey, we apparently can't decide whether or not to let signed measures be infinite. As far as I can tell, the choice does not matter too much. The main results for signed measures, such as Hahn and Jordan decomposition, all hold for signed measures that can take values $\pm \infty$. So they also hold for real-valued signed measures, since this is a smaller class of measures.
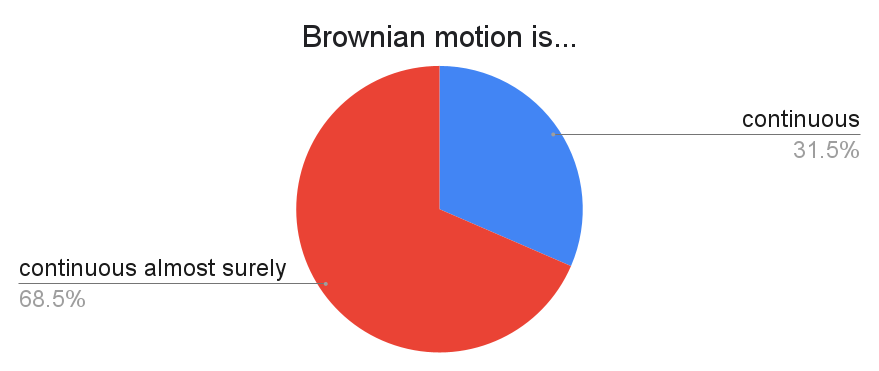
Brownian motion is basically that super duper zig-zaggy thing you see at the stock market. Essentially, if you were to choose a random such zigzaggy path, must you always get a continuous trajectory? Or will this trajectory only be continuous with probability 1? Survey says most people say the latter. As usual, this choice is quite inconsequential.
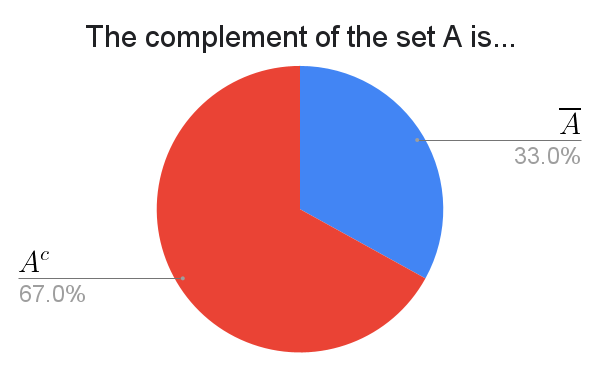
According to Wikipedia, "$A^\complement$" is the standard notation for the complement of $A$.
Sorry but this is the one time I'm going to explicitly voice an opinion on this results page. The reason why $A^c$ is written in the above chart instead of $A^\complement$ is because I think $A^\complement$ is a horrid abominiation that needs to be nuked from orbit. $\complement$ is a visually appalling manifestation of the devil. It is absolutely mortifying to exist in the same plane of reality as the hideous "$\complement$". Just look at it. It has no idea what it wants to be. Its vertical elongation is absolutely jarring. It looks completely different from the letter styles of everything else in LaTeX. $c$, $C$, $\mathcal{C}$, $\mathbb{C}$, $\mathbf{C}$, $\mathsf{C}$, $\mathscr{C}$, and $\mathfrak{C}$ are all beautiful. What the hell is $\complement$??? I'll tell you what it is: It's an atrocity. It's a war crime. It is NOT welcome in the math typesetting family and needs to be exiled to the black hole from whence it came. I yearn for the day when $\complement$ will be abolished. With your help, we can make it happen.
Other responses include:
There are more interesting notations listed here.
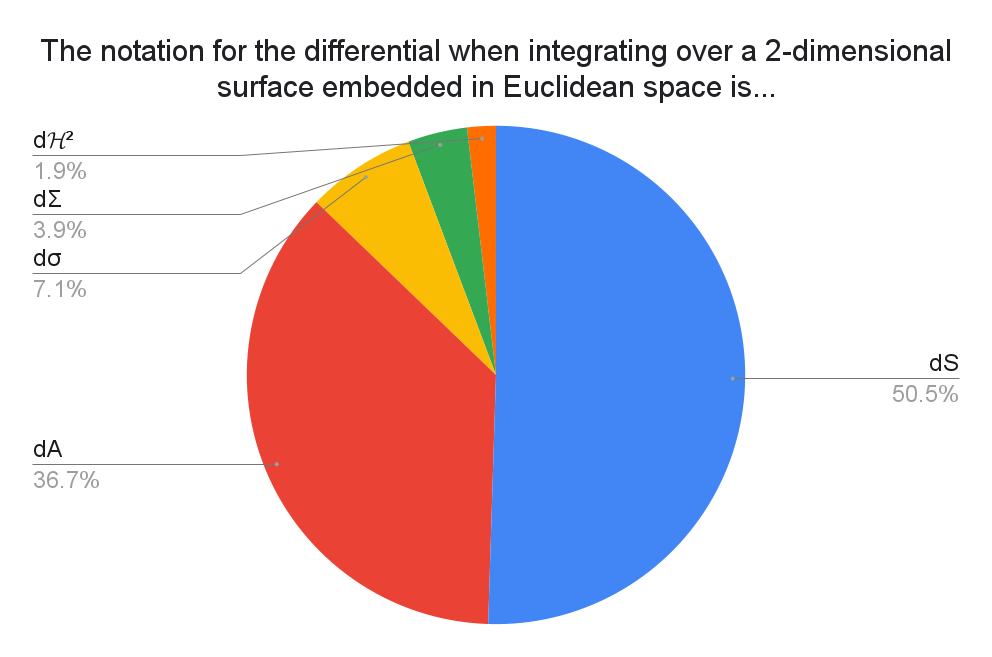
A brief explanation of where the options come from: $dS$, $d\sigma$, $d\Sigma$ likely stem from "Surface", $dA$ surely stems from "Area", and $d\mathcal{H}^2$ indicates the 2-dimensional Hausdorff measure. It would appear that this is mainly a fight between $dS$ and $dA$.
Other responses include:
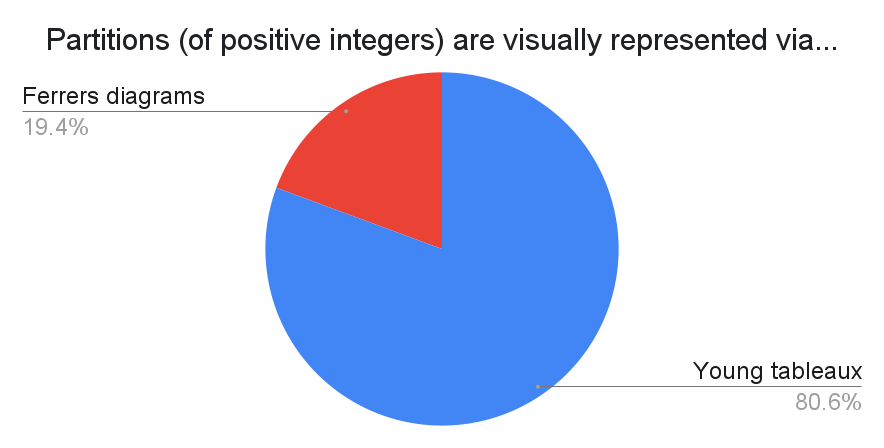
A popular complaint is that it should be Young diagrams, not tableaux. That's my bad. Technically "Young tableaux" are what you get when you fill in the boxes of Young diagrams with numbers or other objects.
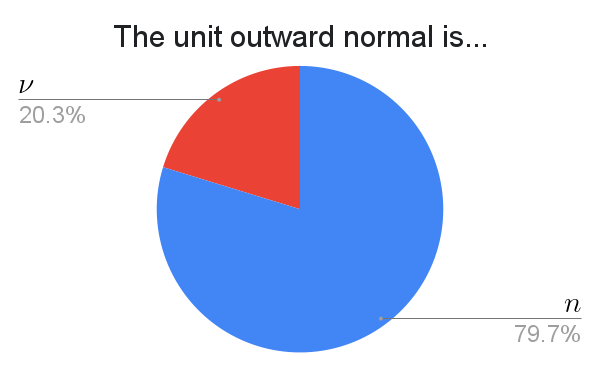
$n$ wins over the Greek $\nu$. Other responses include:
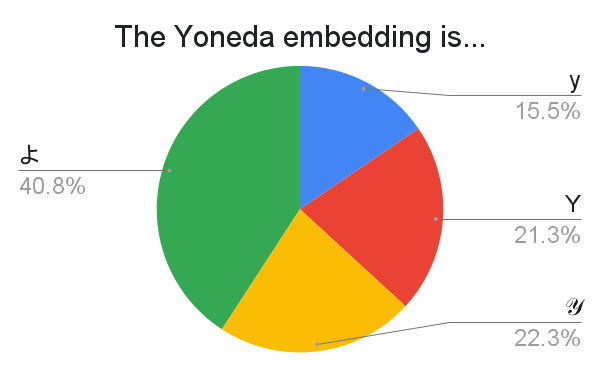
None of the choices are considerably unpopular, but the Japanese hiragana よ is the clear winner! The undergrads reading should consider taking a course in category theory if only because it's the only time where you get a very good excuse to use a Japanese character for a variable name.
Two respondents wrote "$h$". That's interesting.
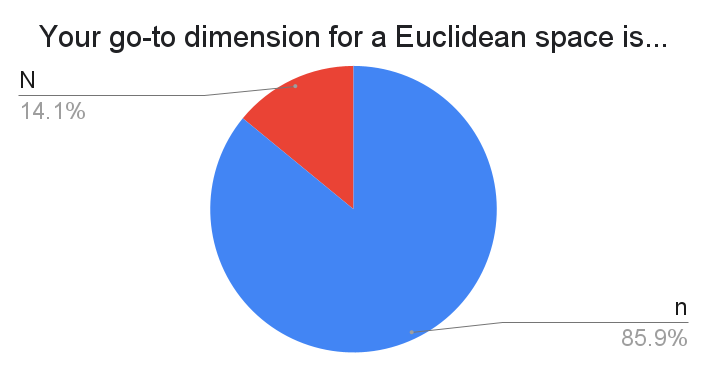
I think one reason for $N$ is so that $n$ is freed up for indices. Four respondents preferred $d$.
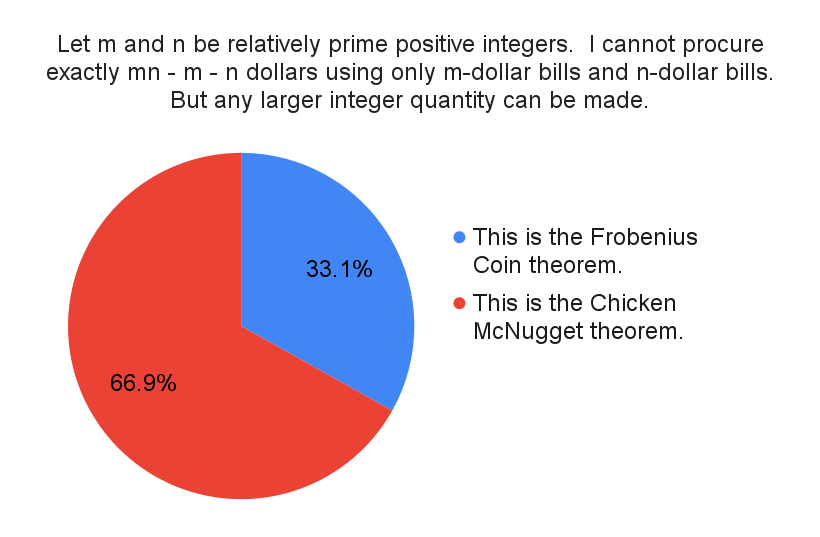
I'm not aware of any one person responsible for popularizing the name "Chicken McNugget". It originated from a time when McDonalds sold their nuggets in boxes of either $9$ nuggets or $20$ nuggets. Using number theory, this means that the largest number of chicken nuggets that you cannot buy is $(9)(20) - 9 - 20 = 151$.
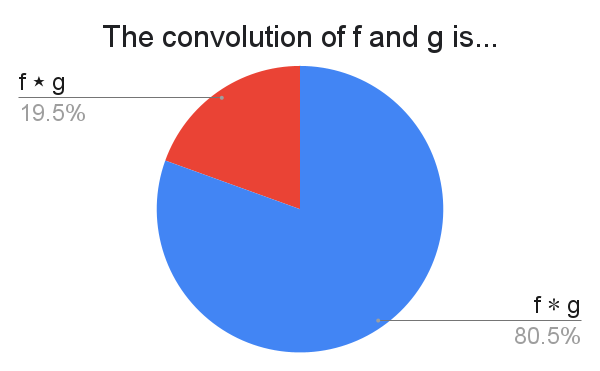
Apparently, as noted by one respondent, there exist people that write $f \times g$. If you don't believe me, look at page 228 of $C^*$ Algebras and their Automorphism Groups by G. K. Pedersen. Quoting Pedersen on that page, "We use $\times$ for convolution instead of the usual $\ast$ to avoid confusion with the adjoint operation." (Yes, I scrolled through a textbook in a subject I know nothing about for half an hour just for this bit. You're welcome.)
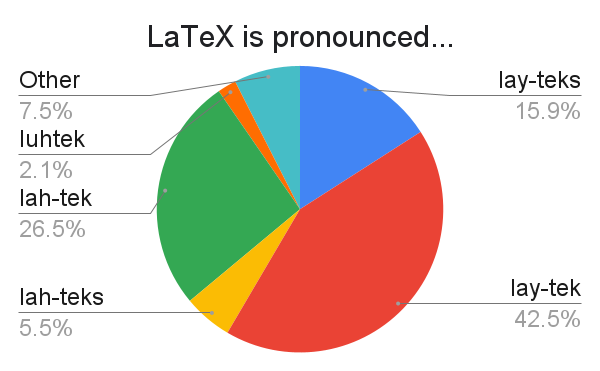
I didn't write these in IPA because I can't read IPA (and I imagine a bunch of respondents wouldn't have bothered to figure it out on the spot either; I wanted to maximize accessibility). So I hope these approximations were clear enough in intent. It appears that the popular choices are "lay-tek", "lah-tek", and "lay-teks", in that order.
Several respondents wrote something about an "unvoiced velar fricative". Several mention a "German -ch". A few respondents pronounce the "TeX" part as "-tesh".
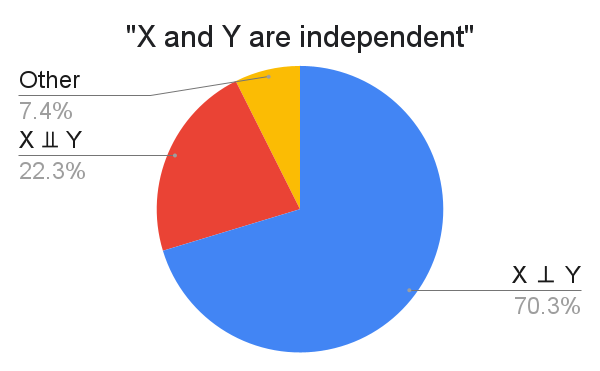
Most of the "Other" responses stated they did not have a symbol, and several were quite passionate that there should be no symbol.
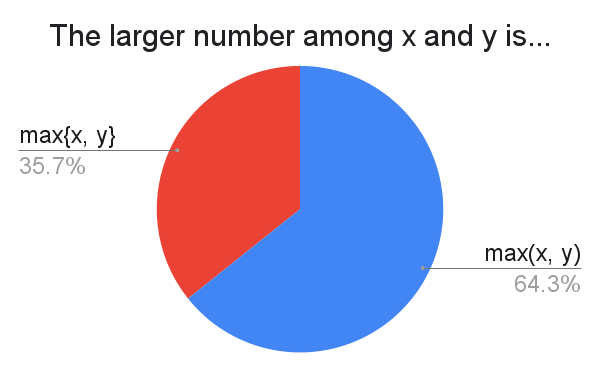
A few people preferred to use $x \lor y$. $\land$ and $\lor$ for min and max might be more common in probability, since it makes the stopped process $X_{n \land \tau}$ (for $\tau$ a stopping time) neater to write.
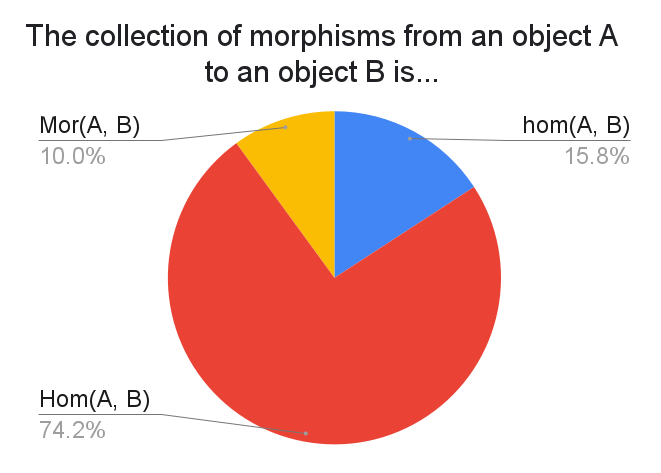
About a dozen preferred $C(A,B)$ where $C$ is the name of the category in question.
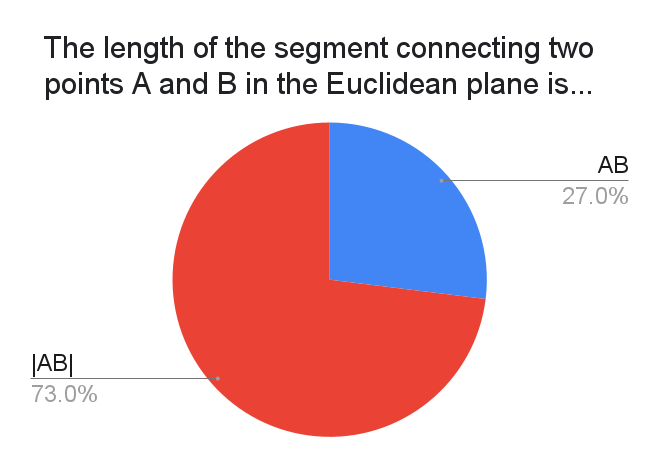
I specified the Euclidean plane because I intended for this to be an elementary geometry question, not a "normed space" question. So I did not consider write-ins such as $\|A-B\|$.
The write-ins bore interesting fruit nevertheless. A couple dozen respondents wrote $\overline{AB}$ and about a dozen wrote $|\overline{AB}|$. I believe $\overline{AB}$ may be quite vomit-inducing to many Americans, that define $\overline{AB}$ to be the segment itself rather than its length. See e.g. Math Open Reference.

In my experience, I see $f(x,-)$ more often in algebraic-flavored fields, whereas I see $f(x,\cdot)$ more among the analysts. I don't know if this generalizes.
Other responses include:
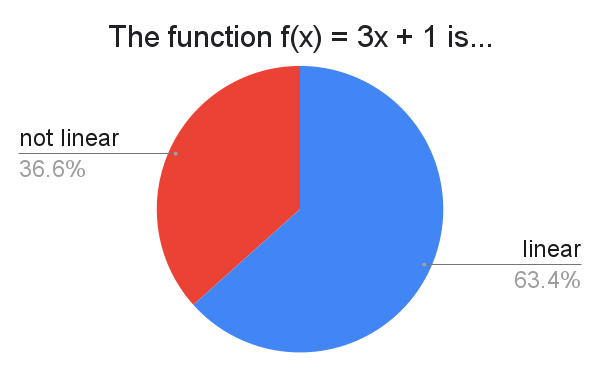
In grade school, it is widely taught that "linear functions" are functions of the form $f(x) = mx+b$. So it is no surprise that the majority says $3x+1$ is linear.
What may surprise quite a lot of people is that a significant fraction of the voters say that $3x+1$ is not linear. Why? This is because in a wide array of contexts in higher math, a linear function or map refers to a function $f$ that satisfies the linearity condition $f(sx+ty) = sf(x)+tf(y)$ for all $x$ and $y$ and for all scalars $s$ and $t$. The first time this comes up is usually in linear algebra, where the (finite dimensional) linear maps are essentially what matrices are. In this view, the only linear functions $f:\mathbb{R} \to \mathbb{R}$ are those that take the form $f(x) = ax$ for some $a \in \mathbb{R}$. Functions such as $3x+1$ are then called affine instead.
Or maybe you knew all of that and answered "linear" anyway, which is totally reasonable. After all, the real villain here is the word "linear" itself, which really shouldn't be the sort of term with contradictory definitions... and yet here we are!
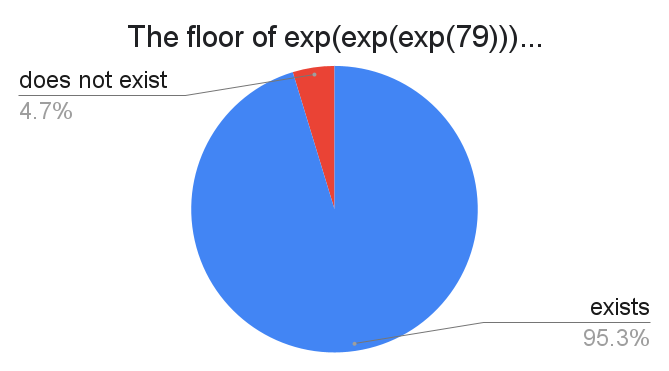
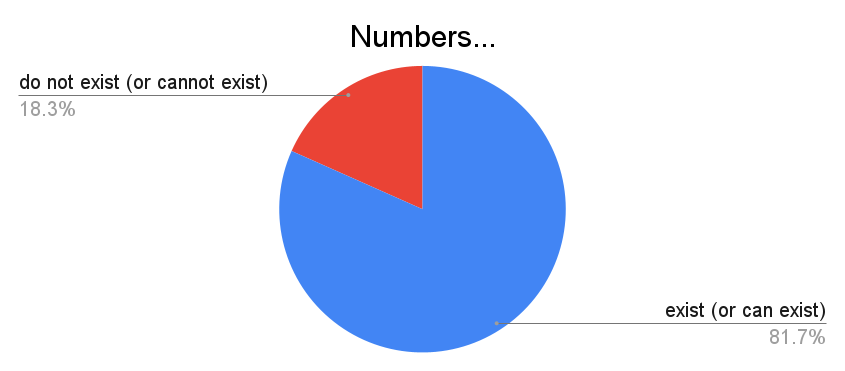
This may seem like a pointless question, with the obvious answer being "yes". You may be surprised to find that not everyone agrees!
The question was about ultrafinitism, which is a matter of mathematical philosophy. Numbers such as $3$ and $4$ exist because they can be represented in the real world --- say, by having 3 apples or 4 grains of sand. But is a number such as $\left\lfloor e^{e^{e^{79}}}\right\rfloor$ too big to exist?
It's difficult to quantify precisely what fraction of respondents were actually ultrafinitists due to sources of error. Nevertheless, the results and comments do seem to suggest that there exist a few ultrafinitists among the respondents. A few respondents commented that $\left\lfloor e^{e^{e^{79}}}\right\rfloor$ exists, but with some... caveats? *shrug*
(A reader pointed out an odd observation when Q20 and Q99 are compared: There are clearly people that chose both "numbers do not exist" and "$\left\lfloor e^{e^{e^{79}}}\right\rfloor$ exists". My guess is that this is because such people interpreted the words "exists" differently in each question (philosophically in the former, mathematically in the latter). You can find a breakdown table in the 91-100 page of the data sheet.)
Thanks for reading!