[1]   Bharat Adsul, Jugal Garg, Ruta Mehta, and Milind Sohoni: Rank-1 bimatrix games: A homeomorphism and a polynomial time algorithm. In Proc. 43rd STOC, pp. 195–204. ACM Press, 2011. [doi:10.1145/1993636.1993664, arXiv:1010.3083]

[2]   Michele Aghassi and Dimitris Bertsimas: Robust game theory. Math. Program., 107(1-2):231–273, 2006. [doi:10.1007/s10107-005-0686-0]

[3]   Haris Angelidakis, Konstantin Makarychev, and Yury Makarychev: Algorithms for stable and perturbation-resilient problems. In Proc. 49th STOC, pp. 438–451. ACM Press, 2017. [doi:10.1145/3055399.3055487]

[4]   Pranjal Awasthi and Maria-Florina Balcan: Center based clustering: A foundational perspective. In Hennig, Meila, Murtagh, and Rocci, editors, Handbook of Cluster Analysis. CRC Press, 2015. Available from CMU.

[5]   Pranjal Awasthi, Maria-Florina Balcan, Avrim Blum, Or Sheffet, and Santosh Vempala: On Nash-equilibria of approximation-stable games. In Proc. 3rd Internat. Symp. Algorithmic Game Theory (SAGT’10), pp. 78–89, 2010. [doi:10.1007/978-3-642-16170-4_8]

[6]   Pranjal Awasthi, Maria-Florina Balcan, Avrim Blum, Or Sheffet, and Santosh Vempala: On Nash-equilibria of approximation-stable games. Current Science J., 103(9):1014–1020, 2012. Available at JSTOR. Preliminary version in SAGT’10.

[7]   Pranjal Awasthi, Avrim Blum, and Or Sheffet: Center-based clustering under perturbation stability. Inform. Process. Lett., 112(1-2):49–54, 2012. [doi:10.1016/j.ipl.2011.10.006, arXiv:1009.3594]

[8]   Maria-Florina Balcan, Avrim Blum, and Anupam Gupta: Approximate clustering without the approximation. In Proc. 20th Ann. ACM-SIAM Symp. on Discrete Algorithms (SODA’09), pp. 1068–1077. ACM Press, 2009. [doi:10.1137/1.9781611973068.116]

[9]   Maria-Florina Balcan, Avrim Blum, and Anupam Gupta: Clustering under approximation stability. J. ACM, 60(2):8:1–8:34, 2013. [doi:10.1145/2450142.2450144]

[10]   Maria-Florina Balcan, Nika Haghtalab, and Colin White: k-center clustering under perturbation resilience. In Proc. 43rd Internat. Colloq. on Automata, Languages and Programming (ICALP’16), volume 55 of LIPIcs, pp. 68:1–68:14. Schloss Dagstuhl, 2016. [doi:10.4230/LIPIcs.ICALP.2016.68, arXiv:1505.03924]

[11]   Maria-Florina Balcan and Yingyu Liang: Clustering under perturbation resilience. SIAM J. Comput., 45(1):102–155, 2016. Preliminary version in ICALP’12. [doi:10.1137/140981575, arXiv:1112.0826]

[12]   Imre Bárány, Santosh Vempala, and Adrian Vetta: Nash equilibria in random games. Random Struct. Algorithms, 31(4):391–405, 2007. Preliminary version in FOCS’05. [doi:10.1002/rsa.20199]

[13]   Yonatan Bilu and Nathan Linial: Are stable instances easy? Combinatorics, Probab. Comput., 21(5):643–660, 2012. Preliminary version appeared in ICS 2010. [doi:10.1017/S0963548312000193, arXiv:0906.3162]

[14]   Hartwig Bosse, Jaroslaw Byrka, and Evangelos Markakis: New algorithms for approximate Nash equilibria in bimatrix games. Theor. Comput. Sci., 411(1):164–173, 2010. Preliminary version in WINE’07. [doi:10.1016/j.tcs.2009.09.023]

[15]   Xi Chen and Xiaotie Deng: Settling the complexity of two-player Nash equilibrium. In Proc. 47th FOCS, pp. 261–272. IEEE Comp. Soc. Press, 2006. [doi:10.1109/FOCS.2006.69, arXiv:0704.1678]

[16]   Xi Chen, Xiaotie Deng, and Shang-Hua Teng: Settling the complexity of computing two-player Nash equilibria. J. ACM, 56(3):14:1–14:57, 2009. [doi:10.1145/1516512.1516516, arXiv:0704.1678]

[17]   Constantinos Daskalakis: On the complexity of approximating a Nash equilibrium. ACM Trans. Algorithms, 9(3):23:1–23:35, 2013. Preliminary version in SODA’11. [doi:10.1145/2483699.2483703]

[18]   Constantinos Daskalakis, Paul W. Goldberg, and Christos H. Papadimitriou: The complexity of computing a Nash equilibrium. SIAM J. Comput., 39(1):195–259, 2009. Preliminary version in STOC’06. [doi:10.1137/070699652]

[19]   Constantinos Daskalakis, Aranyak Mehta, and Christos H. Papadimitriou: Progress in approximate Nash equilibria. In Proc. 8th ACM Conf. on Electronic Commerce (EC’07), pp. 355–358, 2007. [doi:10.1145/1250910.1250962]

[20]   Constantinos Daskalakis, Aranyak Mehta, and Christos H. Papadimitriou: A note on approximate Nash equilibria. Theoret. Comput. Sci., 410(17):1581–1588, 2009. Preliminary version in WINE’06. [doi:10.1016/j.tcs.2008.12.031]

[21]   Luc Devroye, László Gy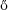rfi, and Gábor Lugosi: A Probabilistic Theory of Pattern Recognition. Springer, 1996. [doi:10.1007/978-1-4612-0711-5]

[22]   Steven N. Durlauf and Lawrence E. Blume: Game Theory. Palgrave Macmillan, 2008. [doi:10.1057/9780230280847]

[23]   Tomás Feder, Hamid Nazerzadeh, and Amin Saberi: Approximating Nash equilibria using small-support strategies. In Proc. 8th ACM Conf. on Electronic Commerce (EC’07), pp. 352–354. ACM, 2007. [doi:10.1145/1250910.1250961]

[24]   Rishi Gupta, Tim Roughgarden, and C. Seshadhri: Decompositions of triangle-dense graphs. SIAM J. Comput., 45(2):197–215, 2016. Preliminary version in ITCS’14. [doi:10.1137/140955331, arXiv:1309.7440]

[25]   Ravi Kannan and Thorsten Theobald: Games of fixed rank: A hierarchy of bimatrix games. Economic Theory, 42(1):157–173, 2010. Preliminary version in SODA’07. [doi:10.1007/s00199-009-0436-2, arXiv:cs/0511021]

[26]   Spyros C. Kontogiannis, Panagiota N. Panagopoulou, and Paul G. Spirakis: Polynomial algorithms for approximating Nash equilibria of bimatrix games. Theor. Comput. Sci., 410(17):1599–1606, 2009. Preliminary version in WINE’06. [doi:10.1016/j.tcs.2008.12.033]

[27]   Spyros C. Kontogiannis and Paul G. Spirakis: On mutual concavity and strategically-zero-sum bimatrix games. Theor. Comput. Sci., 432:64–76, 2012. Preliminary version in APPROX’10. [doi:10.1016/j.tcs.2012.01.016]

[28]   Richard J. Lipton, Evangelos Markakis, and Aranyak Mehta: Playing large games using simple strategies. In Proc. 4th ACM Conf. on Electronic Commerce (EC’03), pp. 36–41. ACM, 2003. [doi:10.1145/779928.779933]

[29]   Richard J. Lipton, Evangelos Markakis, and Aranyak Mehta: On stability properties of economic solution concepts. Manuscript, 2006.

[30]   Hervé Moulin and Jean-Philippe Vial: Strategically zero-sum games: The class of games whose completely mixed equilibria cannot be improved upon. Internat. J. Game Theory, 7(3–4):201–221, 1978. [doi:10.1007/BF01769190]

[31]   John F. Nash: Non-cooperative games. Ann. of Math., 54(2):286–295, 1951. [doi:10.2307/1969529]

[32]   Aviad Rubinstein: Settling the complexity of computing approximate two-player Nash equilibria. ACM SIGecom Exchanges, 15(2):45–49, 2017. Preliminary version in FOCS’16. [doi:10.1145/3055589.3055596, arXiv:1606.04550]

[33]    Haralampos Tsaknakis and Paul G. Spirakis: An optimization approach for approximate Nash equilibria. Internet Mathematics, 5(4):365–382, 2007. Preliminary version in WINE’07. [doi:10.1080/15427951.2008.10129172]

[34]   Konstantin Voevodski, Maria-Florina Balcan, Heiko Röglin, Shang-Hua Teng, and Yu Xia: Efficient clustering with limited distance information. In Proc. 26th Ann. Conf. on Uncertainty in Artificial Intelligence (UAI’10), pp. 632–640. AUAI Press, 2010. Available from AUAI Press. [arXiv:1408.2045]

[35]   John von Neumann and Oskar Morgenstern: Theory of Games and Economic Behavior (60th-Anniversary Edition). Princeton Univ. Press, 2007. [http://press.princeton.edu/titles/7802.html]