[1]   Manindra Agrawal: Proving lower bounds via pseudo-random generators. In Proc. 25th Internat. Conf. on Foundation of Software Tech. and Theoret. Comput. Sci. (FSTTCS’05), volume 3821 of LNCS, pp. 92–105. Springer, 2005. [doi:10.1007/11590156_6]

[2]   Manindra Agrawal, Rohit Gurjar, Arpita Korwar, and Nitin Saxena: Hitting-sets for ROABP and sum of set-multilinear circuits. SIAM J. Comput., 44(3):669–697, 2015. [doi:10.1137/140975103, arXiv:1406.7535]

[3]   Manindra Agrawal, Chandan Saha, and Nitin Saxena: Quasi-polynomial hitting-set for set-depth-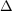 formulas. In Proc. 45th STOC, pp. 321–330. ACM Press, 2013. [doi:10.1145/2488608.2488649, arXiv:1209.2333]

[4]   Matthew Anderson, Michael A. Forbes, Ramprasad Saptharishi, Amir Shpilka, and Ben Lee Volk: Identity testing and lower bounds for read-k oblivious algebraic branching programs. In Proc. 31st IEEE Conf. on Computational Complexity (CCC’16), pp. 30:1–30:25. IEEE Comp. Soc. Press, 2016. [doi:10.4230/LIPIcs.CCC.2016.30, arXiv:1511.07136]

[5]   Sanjeev Arora and Boaz Barak: Computational Complexity: A Modern Approach. Cambridge Univ. Press, 1st edition, 2009. [doi:10.1017/CBO9780511804090]

[6]   Michael Ben-Or and Richard Cleve: Computing algebraic formulas using a constant number of registers. SIAM J. Comput., 21(1):54–58, 1992. Preliminary version in STOC’88. [doi:10.1137/0221006]

[7]   Stuart J. Berkowitz: On computing the determinant in small parallel time using a small number of processors. Inform. Process. Lett., 18(3):147–150, 1984. [doi:10.1016/0020-0190(84)90018-8]

[8]   Andrej Bogdanov, Zeev Dvir, Elad Verbin, and Amir Yehudayoff: Pseudorandomness for width-2 branching programs. Theory of Computing, 9(7):283–293, 2013. [doi:10.4086/toc.2013.v009a007]

[9]   Mark Braverman, Anup Rao, Ran Raz, and Amir Yehudayoff: Pseudorandom generators for regular branching programs. SIAM J. Comput., 43(3):973–986, 2014. Preliminary version in FOCS’10. [doi:10.1137/120875673]

[10]   Joshua Brody and Elad Verbin: The coin problem and pseudorandomness for branching programs. In Proc. 51st FOCS, pp. 30–39. IEEE Comp. Soc. Press, 2010. [doi:10.1109/FOCS.2010.10]

[11]   Anindya De: Pseudorandomness for permutation and regular branching programs. In Proc. 26th IEEE Conf. on Computational Complexity (CCC’11), pp. 221–231. IEEE Comp. Soc. Press, 2011. [doi:10.1109/CCC.2011.23]

[12]   Rafael Mendes de Oliveira, Amir Shpilka, and Ben Lee Volk: Subexponential size hitting sets for bounded depth multilinear formulas. Comput. Complexity, 25(2):455–505, 2016. Preliminary version in CCC’15. [doi:10.1007/s00037-016-0131-1, arXiv:1411.7492]

[13]   Richard A. Demillo and Richard J. Lipton: A probabilistic remark on algebraic program testing. Inform. Process. Lett., 7(4):193 – 195, 1978. [doi:10.1016/0020-0190(78)90067-4]

[14]   Michael A. Forbes, Ramprasad Saptharishi, and Amir Shpilka: Hitting sets for multilinear read-once algebraic branching programs, in any order. In Proc. 46th STOC, pp. 867–875. ACM Press, 2014. [doi:10.1145/2591796.2591816]

[15]   Michael A. Forbes and Amir Shpilka: Quasipolynomial-time identity testing of non-commutative and read-once oblivious algebraic branching programs. In Proc. 54th FOCS, pp. 243–252. IEEE Comp. Soc. Press, 2013. [doi:10.1109/FOCS.2013.34, arXiv:1209.2408]

[16]   Rohit Gurjar, Arpita Korwar, and Nitin Saxena: Identity testing for constant-width, and commutative, read-once oblivious ABPs. In Proc. 31st IEEE Conf. on Computational Complexity (CCC’16), pp. 29:1–29:16. IEEE Comp. Soc. Press, 2016. [doi:10.4230/LIPIcs.CCC.2016.29, arXiv:1601.08031]

[17]   Rohit Gurjar, Arpita Korwar, Nitin Saxena, and Thomas Thierauf: Deterministic identity testing for sum of read-once oblivious arithmetic branching programs. Comput. Complexity, pp. 1–46, 2016. Preliminary version in CCC’15. [doi:10.1007/s00037-016-0141-z, arXiv:1411.7341]

[18]   Joos Heintz and Claus P. Schnorr: Testing polynomials which are easy to compute (extended abstract). In Proc. 12th STOC, pp. 262–272. ACM Press, 1980. [doi:10.1145/800141.804674]

[19]   Russell Impagliazzo, Raghu Meka, and David Zuckerman: Pseudorandomness from shrinkage. In Proc. 53rd FOCS, pp. 111–119. IEEE Comp. Soc. Press, 2012. Preliminary version in ECCC. [doi:10.1109/FOCS.2012.78]

[20]   Russell Impagliazzo, Noam Nisan, and Avi Wigderson: Pseudorandomness for network algorithms. In Proc. 26th STOC, pp. 356–364. ACM Press, 1994. [doi:10.1145/195058.195190]

[21]   Valentine Kabanets and Russell Impagliazzo: Derandomizing polynomial identity tests means proving circuit lower bounds. Comput. Complexity, 13(1):1–46, 2004. Preliminary version in STOC’03. [doi:10.1007/s00037-004-0182-6]

[22]   Neeraj Kayal, Vineet Nair, and Chandan Saha: Separation between read-once oblivious algebraic branching programs (ROABPs) and multilinear depth three circuits. In Proc. 33rd Symp. Theoretical Aspects of Comp. Sci. (STACS’16), pp. 46:1–46:15. Schloss Dagstuhl, 2016. Preliminary version in ECCC. [doi:10.4230/LIPIcs.STACS.2016.46]

[23]   Pascal Koiran: Arithmetic circuits: The chasm at depth four gets wider. Theoret. Comput. Sci., 448:56–65, 2012. [doi:10.1016/j.tcs.2012.03.041, arXiv:1006.4700]

[24]    Michal Koucký, Prajakta Nimbhorkar, and Pavel Pudlák: Pseudorandom generators for group products: extended abstract. In Proc. 43rd STOC, pp. 263–272. ACM Press, 2011. [doi:10.1145/1993636.1993672]

[25]   Noam Nisan: Lower bounds for non-commutative computation (extended abstract). In Proc. 23rd STOC, pp. 410–418. ACM Press, 1991. [doi:10.1145/103418.103462]

[26]   Noam Nisan: Pseudorandom generators for space-bounded computation. Combinatorica, 12(4):449–461, 1992. Preliminary version in STOC’90. [doi:10.1007/BF01305237]

[27]   Ran Raz and Omer Reingold: On recycling the randomness of states in space bounded computation. In Proc. 31st STOC, pp. 159–168. ACM Press, 1999. [doi:10.1145/301250.301294]

[28]   Ran Raz and Amir Shpilka: Deterministic polynomial identity testing in non-commutative models. Comput. Complexity, 14(1):1–19, 2005. Preliminary version in CCC’04. [doi:10.1007/s00037-005-0188-8]

[29]   Jacob T. Schwartz: Fast probabilistic algorithms for verification of polynomial identities. J. ACM, 27(4):701–717, 1980. Preliminary version in EUROSAM’79. [doi:10.1145/322217.322225]

[30]   Thomas Steinke: Pseudorandomness for permutation branching programs without the group theory. Electron. Colloq. on Comput. Complexity (ECCC), 19(83), 2012. Available at ECCC.

[31]   Leslie G. Valiant: Completeness classes in algebra. In Proc. 11th STOC, pp. 249–261. ACM Press, 1979. [doi:10.1145/800135.804419]

[32]   Leslie G. Valiant, Sven Skyum, Stuart J. Berkowitz, and Charles Rackoff: Fast parallel computation of polynomials using few processors. SIAM J. Comput., 12(4):641–644, 1983. Preliminary version in MFCS’81. [doi:10.1137/0212043]

[33]   Richard Zippel: Probabilistic algorithms for sparse polynomials. In Proc. Internat. Symp. Symbolic and Algebraic Comput. (EUROSAM’79), pp. 216–226. Springer, 1979. [doi:10.1007/3-540-09519-5_73]