[1]   Scott Aaronson: Quantum lower bound for the collision problem. In Proc. 34th STOC, pp. 635–642. ACM Press, 2002. [doi:10.1145/509907.509999]

[2]   Scott Aaronson: The polynomial method in quantum and classical computing. In Proc. 49th FOCS, p. 3. IEEE Comp. Soc. Press, 2008. [doi:10.1109/FOCS.2008.91]

[3]   Scott Aaronson: The collision problem: Notes for lecture 13 of MIT course 6.845: Quantum complexity theory, 2010. Available at MIT OCW.

[4]   Scott Aaronson: The collision lower bound after 12 years, 2013. Available on author’s website.

[5]   Scott Aaronson and Yaoyun Shi: Quantum lower bounds for the collision and the element distinctness problems. J. ACM, 51(4):595–605, 2004. [doi:10.1145/1008731.1008735]

[6]   Andris Ambainis: Quantum lower bounds by quantum arguments. J. Comput. System Sci., 64(4):750–767, 2002. Preliminary version in STOC’00. [doi:10.1006/jcss.2002.1826, arXiv:quant-ph/0002066]

[7]   Andris Ambainis: Polynomial degree and lower bounds in quantum complexity: Collision and element distinctness with small range. Theory of Computing, 1(3):37–46, 2005. [doi:10.4086/toc.2005.v001a003, arXiv:quant-ph/0305179]

[8]   Andris Ambainis: Polynomial degree vs. quantum query complexity. J. Comput. System Sci., 72(2):220–238, 2006. Preliminary version in FOCS’03. [doi:10.1016/j.jcss.2005.06.006, arXiv:quant-ph/0305028]

[9]   Andris Ambainis: Quantum walk algorithm for element distinctness. SIAM J. Comput., 37(1):210–239, 2007. Preliminary version in FOCS’04. [doi:10.1137/S0097539705447311, arXiv:quant-ph/0311001]

[10]   Howard Barnum, Michael E. Saks, and Mario Szegedy: Quantum query complexity and semi-definite programming. In Proc. 18th IEEE Conf. on Computational Complexity (CCC’03), pp. 179–193. IEEE Comp. Soc. Press, 2003. [doi:10.1109/CCC.2003.1214419]

[11]   Robert Beals, Harry Buhrman, Richard Cleve, Michele Mosca, and Ronald de Wolf: Quantum lower bounds by polynomials. J. ACM, 48(4):778–797, 2001. Preliminary version in FOCS’98. [doi:10.1145/502090.502097, arXiv:quant-ph/9802049]

[12]   Richard Beigel: The polynomial method in circuit complexity. In Proc. 8th IEEE Conf. on Structure in Complexity Theory (SCT’93), pp. 82–95. IEEE Comp. Soc. Press, 1993. [doi:10.1109/SCT.1993.336538]

[13]   Richard Beigel: Perceptrons, PP, and the polynomial hierarchy. Comput. Complexity, 4(4):339–349, 1994. Preliminary version in SCT’92. [doi:10.1007/BF01263422]

[14]   Aleksandrs Belovs and Ansis Rosmanis: Adversary lower bounds for the collision and the set equality problems, 2013. [arXiv:1310.5185]

[15]   Aleksandrs Belovs and Robert Špalek: Adversary lower bound for the k-sum problem. In Proc. 4th Conf. on Innovations in Theoret. Comput. Sci. (ITCS’13), pp. 323–328. ACM Press, 2013. [doi:10.1145/2422436.2422474, arXiv:1206.6528]

[16]   Andrej Bogdanov, Yuval Ishai, Emanuele Viola, and Christopher Williamson: Bounded indistinguishability and the complexity of recovering secrets. In Proc. of 36th Internat. Cryptology Conf. (CRYPTO’16), volume 9816 of LNCS, pp. 593–618. Springer, 2016. Available at ECCC. [doi:10.1007/978-3-662-53015-3_21]

[17]   Gilles Brassard, Peter Høyer, and Alain Tapp: Quantum algorithm for the collision problem. In Encyclopedia of Algorithms, pp. 1–99. Springer, 2008. Preliminary version in ACM SIGACT News. [doi:10.1007/978-0-387-30162-4_304, arXiv:quant-ph/9705002]

[18]   Harry Buhrman, Nikolai K. Vereshchagin, and Ronald de Wolf: On computation and communication with small bias. In Proc. 22nd IEEE Conf. on Computational Complexity (CCC’07), pp. 24–32. IEEE Comp. Soc. Press, 2007. [doi:10.1109/CCC.2007.18]

[19]   Mark Bun and Justin Thaler: Dual lower bounds for approximate degree and Markov-Bernstein inequalities. Inform. and Comput., 243:2–25, 2015. Preliminary version in ICALP’13. [doi:10.1016/j.ic.2014.12.003, arXiv:1302.6191]

[20]   Mark Bun and Justin Thaler: Hardness amplification and the approximate degree of constant-depth circuits. In Proc. 42nd Internat. Colloq. on Automata, Languages and Programming (ICALP’15), volume 9134 of LNCS, pp. 268–280. Springer, 2015. [doi:10.1007/978-3-662-47672-7_22, arXiv:1311.1616]

[21]   Karthekeyan Chandrasekaran, Justin Thaler, Jonathan Ullman, and Andrew Wan: Faster private release of marginals on small databases. In Proc. 5th Conf. on Innovations in Theoret. Comput. Sci. (ITCS’14), pp. 387–402. ACM Press, 2014. [doi:10.1145/2554797.2554833, arXiv:1304.3754]

[22]   Peter Høyer, Troy Lee, and Robert Spalek: Negative weights make adversaries stronger. In Proc. 39th STOC, pp. 526–535. ACM Press, 2007. [doi:10.1145/1250790.1250867, arXiv:quant-ph/0611054]

[23]   Peter Høyer, Michele Mosca, and Ronald de Wolf: Quantum search on bounded-error inputs. In Proc. 30th Internat. Colloq. on Automata, Languages and Programming (ICALP’03), volume 2719 of LNCS, pp. 291–299. Springer, 2003. [doi:10.1007/3-540-45061-0_25, arXiv:quant-ph/0304052]

[24]   Adam Tauman Kalai, Adam R. Klivans, Yishay Mansour, and Rocco A. Servedio: Agnostically learning halfspaces. SIAM J. Comput., 37(6):1777–1805, 2008. Preliminary version in FOCS’05. [doi:10.1137/060649057]

[25]   Varun Kanade and Justin Thaler: Distribution-independent reliable learning. In Proc. 27th Ann. Conf. on Learning Theory (COLT’14), pp. 3–24, 2014. JMLR. [arXiv:1402.5164]

[26]   Adam R. Klivans and Rocco A. Servedio: Learning DNF in time 2^Õ(n1∕3) . J. Comput. System Sci., 68(2):303–318, 2004. Preliminary version in STOC’01. [doi:10.1016/j.jcss.2003.07.007]

[27]   Adam R. Klivans and Rocco A. Servedio: Toward attribute efficient learning of decision lists and parities. J. Machine Learning Res., 7:587–602, 2006. JMLR. Preliminary version in COLT’04.

[28]   Samuel Kutin: Quantum lower bound for the collision problem with small range. Theory of Computing, 1(2):29–36, 2005. [doi:10.4086/toc.2005.v001a002]

[29]   Loïck Magnin and Jérémie Roland: Explicit relation between all lower bound techniques for quantum query complexity. Internat. J. Quantum Inform., 13(4):1350059, 2015. Preliminary versions in STACS’13 and ECCC. [doi:10.1142/S0219749913500597, arXiv:1209.2713]

[30]   Noam Nisan and Mario Szegedy: On the degree of boolean functions as real polynomials. Comput. Complexity, 4(4):301–313, 1994. Preliminary version in STOC’92. [doi:10.1007/BF01263419]

[31]   Ryan O’Donnell and Rocco A. Servedio: New degree bounds for polynomial threshold functions. Combinatorica, 30(3):327–358, 2010. Preliminary version in STOC’03. [doi:10.1007/s00493-010-2173-3]

[32]   Ramamohan Paturi: On the degree of polynomials that approximate symmetric boolean functions (preliminary version). In Proc. 24th STOC, pp. 468–474. ACM Press, 1992. [doi:10.1145/129712.129758]

[33]   Ben W. Reichardt: Span programs and quantum query complexity: The general adversary bound is nearly tight for every boolean function. In Proc. 50th FOCS, pp. 544–551. IEEE Comp. Soc. Press, 2009. [doi:10.1109/FOCS.2009.55, arXiv:0904.2759]

[34]   Ben W. Reichardt: Reflections for quantum query algorithms. In Proc. 22nd Ann. ACM-SIAM Symp. on Discrete Algorithms (SODA’11), pp. 560–569. ACM Press, 2011. [doi:10.1137/1.9781611973082.44, arXiv:1005.1601]

[35]   Rocco A. Servedio, Li-Yang Tan, and Justin Thaler: Attribute-efficient learning and weight-degree tradeoffs for polynomial threshold functions. In Proc. 25th Ann. Conf. on Learning Theory (COLT’12), volume 23, pp. 14.1–14.19, 2012. JMLR.

[36]   Alexander A. Sherstov: Communication lower bounds using dual polynomials. Bulletin of the EATCS, 95:59–93, 2008. Available at EATCS. [arXiv:0805.2135]

[37]   Alexander A. Sherstov: Separating AC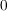 from depth-2 majority circuits. SIAM J. Comput., 38(6):2113–2129, 2009. Preliminary version in STOC’07. [doi:10.1137/08071421X]

[38]   Alexander A. Sherstov: The pattern matrix method. SIAM J. Comput., 40(6):1969–2000, 2011. Preliminary version in STOC’08. [doi:10.1137/080733644, arXiv:0906.4291]

[39]   Alexander A. Sherstov: Strong direct product theorems for quantum communication and query complexity. SIAM J. Comput., 41(5):1122–1165, 2011. Preliminary version in STOC’11. [doi:10.1137/110842661, arXiv:1011.4935]

[40]   Alexander A. Sherstov: Approximating the AND-OR tree. Theory of Computing, 9(20):653–663, 2013. Preliminary version in ECCC. [doi:10.4086/toc.2013.v009a020]

[41]   Alexander A. Sherstov: The intersection of two halfspaces has high threshold degree. SIAM J. Comput., 42(6):2329–2374, 2013. Preliminary versions in FOCS’09 and ECCC. [doi:10.1137/100785260, arXiv:0910.1862]

[42]   Alexander A. Sherstov: Breaking the Minsky-Papert barrier for constant-depth circuits. In Proc. 46th STOC, pp. 223–232. ACM Press, 2014. Also available at ECCC. [doi:10.1145/2591796.2591871]

[43]   Alexander A. Sherstov: The power of asymmetry in constant-depth circuits. In Proc. 56th FOCS, pp. 431–450. IEEE Comp. Soc. Press, 2015. Also available at ECCC. [doi:10.1109/FOCS.2015.34]

[44]   Yaoyun Shi: Quantum lower bounds for the collision and the element distinctness problems. In Proc. 43rd FOCS, pp. 513–519. IEEE Comp. Soc. Press, 2002. [doi:10.1109/SFCS.2002.1181975, arXiv:quant-ph/0112086]

[45]   Yaoyun Shi and Yufan Zhu: Quantum communication complexity of block-composed functions. Quantum Inf. Comput., 9(5):444–460, 2009. ACM DL. [arXiv:0710.0095]

[46]   Robert Špalek: A dual polynomial for OR, 2008. [arXiv:0803.4516]

[47]   Robert Špalek and Mario Szegedy: All quantum adversary methods are equivalent. Theory of Computing, 2(1):1–18, 2006. Preliminary version in ICALP’05. [doi:10.4086/toc.2006.v002a001]

[48]   Justin Thaler: Lower bounds for the approximate degree of block-composed functions. Electron. Colloq. on Comput. Complexity (ECCC), 21(150), 2014. ECCC.

[49]   Justin Thaler, Jonathan Ullman, and Salil P. Vadhan: Faster algorithms for privately releasing marginals. In Proc. 39th Internat. Colloq. on Automata, Languages and Programming (ICALP’12), volume 7391 of LNCS, pp. 810–821. Springer, 2012. [doi:10.1007/978-3-642-31594-7_68, arXiv:1205.1758]

[50]   Henry Yuen: A quantum lower bound for distinguishing random functions from random permutations. Quantum Inf. Comput., 14(13-14):1089–1097, 2014. ACM DL. [arXiv:1310.2885]

[51]   Mark Zhandry: A note on the quantum collision and set equality problems. Quantum Inf. Comput., 15(7-8):557–567, 2015. ACM DL. [arXiv:1312.1027]

[52]   Shengyu Zhang: On the power of Ambainis lower bounds. Theoret. Comput. Sci., 339(2-3):241–256, 2005. Preliminary version in ICALP’04. [doi:10.1016/j.tcs.2005.01.019, arXiv:quant-ph/0311060]