[1]   Noga Alon, Baruch Awerbuch, Yossi Azar, Niv Buchbinder, and Joseph (Seffi) Naor: The online set cover problem. SIAM J. Comput., 39(2):361–370, 2009. Preliminary version in STOC’03. [doi:10.1137/060661946]

[2]   Noga Alon and Joel H. Spencer: The Probabilistic Method. John Wiley, 1992. [doi:10.1002/9780470277331]

[3]   Sanjeev Arora, Elad Hazan, and Satyen Kale: Fast algorithms for approximate semidefinite programming using the multiplicative weights update method. In Proc. 46th FOCS, pp. 339–348. IEEE Comp. Soc. Press, 2005. [doi:10.1109/SFCS.2005.35]

[4]   Sanjeev Arora, Elad Hazan, and Satyen Kale: O(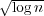) approximation to SPARSEST CUT in Õ(n²) time. SIAM J. Comput., 39:1748–1771, 2010. Preliminary version in FOCS’04. [doi:10.1137/080731049]

[5]   Sanjeev Arora and Satyen Kale: A combinatorial, primal-dual approach to semidefinite programs. In Proc. 39th STOC, pp. 227–236. ACM Press, 2007. [doi:10.1145/1250790.1250823]

[6]   Sanjeev Arora, James R. Lee, and Assaf Naor: Euclidean distortion and the sparsest cut. J. Amer. Math. Soc., 21:1–21, 2008. Preliminary version in STOC’05. [doi:10.1090/S0894-0347-07-00573-5]

[7]   Sanjeev Arora, Satish Rao, and Umesh Vazirani: Expander flows, geometric embeddings, and graph partitioning. J. ACM, 56(2):5:1–5:37, 2009. Preliminary version in 36th STOC (2004). [doi:10.1145/1502793.1502794]

[8]   Boaz Barak, Moritz Hardt, and Satyen Kale: The uniform hardcore lemma via approximate Bregman projections. In Proc. 20th Ann. ACM-SIAM Symp. on Discrete Algorithms (SODA’09), pp. 1193–1200. ACM Press, 2009. [ACM DL] [SIAM PDF].

[9]   András A. Benczúr and David R. Karger: Approximating s - t minimum cuts in Õ(n²) time. In Proc. 28th STOC, pp. 47–55. ACM Press, 1996. [doi:10.1145/237814.237827]

[10]   Avrim Blum: On-line algorithms in machine learning. In A. Fiat and G. Woeginger, editors, Online Algorithms: The State of the Art, pp. 306–325. LNCS 1442, 1998. [doi:10.1007/BFb0029575]

[11]   H. Brönnimann and M.T. Goodrich: Almost optimal set covers in finite VC-dimension. Discrete Comput. Geom., 14:463–479, 1995. Preliminary version in 10th Ann. Symp. Comp. Geom. (SCG’94). [doi:10.1007/BF02570718]

[12]   George W. Brown: Iterative solution of games by fictitious play. In T. C. Koopmans, editor, Analysis of Production and Allocation, pp. 374–376. Wiley, 1951.

[13]   George W. Brown and John von Neumann: Solutions of games by differential equations. Annals of Mathematics Studies, 24:73–79, 1950.

[14]   Niv Buchbinder and Joseph (Seffi) Naor: The design of competitive online algorithms via a primal-dual approach. Foundations and Trends in Theoretical Computer Science, 3(2-3):93–263, 2009. [doi:10.1561/0400000024]

[15]   Niv Buchbinder and Joseph (Seffi) Naor: Online primal-dual algorithms for covering and packing. Math. Oper. Res., 34(2):270–286, 2009. [doi:10.1287/moor.1080.0363]

[16]    Nicolò Cesa-Bianchi and Gábor Lugosi: Prediction, Learning, and Games. Cambridge University Press, 2006. [doi:10.1017/CBO9780511546921]

[17]   Nicolò Cesa-Bianchi, Yishay Mansour, and Gilles Stoltz: Improved second-order bounds for prediction with expert advice. Machine Learning, 66(2-3):321–352, 2007. [doi:10.1007/s10994-006-5001-7]

[18]   Suchi Chawla, Anupam Gupta, and Harald Räcke: Embeddings of negative-type metrics and an improved approximation to generalized sparsest cut. ACM Trans. Algorithms, 4:22:1–22:18, 2008. Preliminary version in SODA’05. [doi:10.1145/1361192.1361199]

[19]   Bernard Chazelle: The Discrepancy Method—Randomness and Complexity. Cambridge University Press, Cambridge, 2000. [doi:10.1007/3-540-49381-6_1]

[20]   Kenneth L. Clarkson: A Las Vegas algorithm for linear programming when the dimension is small. In Proc. 29th FOCS, pp. 452–456. IEEE Comp. Soc. Press, 1988. [doi:10.1109/SFCS.1988.21961]

[21]   Kenneth L. Clarkson: A Las Vegas algorithm for linear and integer programming when the dimension is small. J. ACM, 42:488–499, 1995. [doi:10.1145/201019.201036]

[22]   Thomas M. Cover: Universal data compression and portfolio selection. In Proc. 37th FOCS, pp. 534–538. IEEE Comp. Soc. Press, 1996. [doi:10.1109/SFCS.1996.548512]

[23]   Uriel Feige: A threshold of lnn for approximating set cover. J. ACM, 45(4):634–652, July 1998. [doi:10.1145/285055.285059]

[24]   Lisa K. Fleischer: Approximating fractional multicommodity flow independent of the number of commodities. SIAM Journal of Discrete Mathematics, 13(4):505–520, 2000. Preliminary version in FOCS’99. [doi:10.1137/S0895480199355754]

[25]   Dean P. Foster and Rakesh Vohra: Regret in the on-line decision problem. Games and Economic Behaviour, 29:7–35, 1999. [doi:10.1006/game.1999.0740]

[26]    Yoav Freund and Robert E. Schapire: A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. System Sci., 55(1):119–139, 1997. [doi:10.1006/jcss.1997.1504]

[27]   Yoav Freund and Robert E. Schapire: Adaptive game playing using multiplicative weights. Games and Economic Behavior, 29:79–103, 1999. [doi:10.1006/game.1999.0738]

[28]   Naveen Garg and Rohit Khandekar: Fractional covering with upper bounds on the variables: Solving LPs with negative entries. In Proc. 12th Ann. Europ. Symp. on Algorithms (ESA’04), pp. 371–382, 2004. [doi:10.1007/978-3-540-30140-0_34]

[29]   Naveen Garg and Jochen Könemann: Faster and simpler algorithms for multicommodity flow and other fractional packing problems. In Proc. 39th FOCS, pp. 300–309. IEEE Comp. Soc. Press, 1998. [doi:10.1109/SFCS.1998.743463]

[30]   Naveen Garg and Jochen Könemann: Faster and simpler algorithms for multicommodity flow and other fractional packing problems. SIAM J. Comput., 37:630–652, 2007. [doi:10.1137/S0097539704446232]

[31]   Michel X. Goemans and David P. Williamson: Improved approximation algorithms for maximum cut and satisfiability problems using semidefinite programming. J. ACM, 42(6):1115–1145, 1995. [doi:10.1145/227683.227684]

[32]   Sidney Golden: Lower Bounds for the Helmholtz Function. Physical Review, 137:1127–1128, February 1965. [doi:10.1103/PhysRev.137.B1127]

[33]   Michael D. Grigoriadis and Leonid G. Khachiyan: A sublinear-time randomized approximation algorithm for matrix games. Operations Research Letters, 18:53–58, 1995. [doi:10.1016/0167-6377(95)00032-0]

[34]   James Hannan: Approximation to Bayes risk in repeated plays. In M. Dresher, A. W. Tucker, and P. Wolfe, editors, Contributions to the Theory of Games, volume 3, pp. 97–139. Princeton University Press, 1957.

[35]   Elad Hazan: Efficient Algorithms for Online Convex Optimization and their Applications. PhD thesis, Princeton University, 2006. Technical Report TR-766-06.

[36]   Elad Hazan: Sparse approximate solutions to semidefinite programs. In Proc. 8th Latin Amer. Symp. on Theoretical Informatics (LATIN’08), pp. 306–316, 2008. [doi:10.1007/978-3-540-78773-0_27]

[37]   Elad Hazan, A. Agarwal, and Satyen Kale: Logarithmic regret algorithms for online convex optimization. Machine Learning, 69(2-3):169–192, 2007. [doi:10.1007/s10994-007-5016-8]

[38]   David P. Helmbold, Robert E. Schapire, Yoram Singer, and Manfred K. Warmuth: On-line portfolio selection using multiplicative updates. Mathematical Finance, 8:325–347, 1998. Preliminary version in 13th Int. Conf. on Machine Learning (ICML’96). [doi:10.1111/1467-9965.00058]

[39]   Mark Herbster and Manfred K. Warmuth: Tracking the best expert. Machine Learning, 32(2):151–178, 1998. [doi:10.1023/A:1007424614876]

[40]   Russell Impagliazzo: Hard-core distributions for somewhat hard problems. In Proc. 36th FOCS, pp. 538–545. IEEE Comp. Soc. Press, 1995. [doi:10.1109/SFCS.1995.492584]

[41]   Rahul Jain, Zhengfeng Ji, Sarvagya Upadhyay, and John Watrous: QIP = PSPACE. J. ACM, 58:30:1–30:27, 2011. Preliminary version in STOC’10. [doi:10.1145/2049697.2049704]

[42]   Adam Kalai: Personal communication with Manfred Warmuth, 2009.

[43]   Adam Kalai and Santosh Vempala: Efficient algorithms for online decision problems. J. Comput. System Sci., 71:291–307, 2005. Preliminary version in 16th COLT (2003). [doi:10.1016/j.jcss.2004.10.016]

[44]   Satyen Kale: Efficient Algorithms Using The Multiplicative Weights Update Method. PhD thesis, Princeton University, 2006. Technical Report TR-804-07.

[45]   Satyen Kale: Boosting and hard-core set constructions: A simplified approach. Technical Report TR07-131, Electron. Colloq. on Comput. Complexity (ECCC), 2007. [ECCC:TR07-131]

[46]   Rohit Khandekar: Lagrangian Relaxation based Algorithms for Convex Programming Problems. PhD thesis, Indian Institute of Technology, Delhi, 2004.

[47]   Philip N. Klein and Hsueh-I Lu: Efficient approximation algorithms for semidefinite programs arising from MAX CUT and COLORING. In Proc. 28th STOC, pp. 338–347. ACM Press, 1996. [doi:10.1145/237814.237980]

[48]   Philip N. Klein and Neal Young: On the number of iterations for Dantzig-Wolfe optimization and packing-covering approximation algorithms. In Proc. 7th Conf. on Integer Programming and Combinatorial Optimization (IPCO’99), LNCS 1610, pp. 320–327. Springer, 1999. [ACM DL].

[49]   Adam R. Klivans and Rocco A. Servedio: Boosting and hard-core set construction. Machine Learning, 51(3):217–238, 2003. [doi:10.1023/A:1022949332276]

[50]   Nick Littlestone: Learning quickly when irrelevant attributes abound: A new linear-threshold algorithm. Machine Learning, 2(4):285–318, 1987. Preliminary version in FOCS’87. [doi:10.1007/BF00116827]

[51]   Nick Littlestone: Mistake bounds and logarithmic linear-threshold learning algorithms. PhD thesis, University of California at Santa Cruz, Santa Cruz, CA, USA, 1989.

[52]   Nick Littlestone and Manfred K. Warmuth: The weighted majority algorithm. Inform. and Comput., 108(2):212–261, 1994. [doi:10.1006/inco.1994.1009]

[53]   Michael Luby and Noam Nisan: A parallel approximation algorithm for positive linear programming. In Proc. 25th STOC, pp. 448–457. ACM Press, 1993. [doi:10.1145/167088.167211]

[54]   Jiři Matoušek and Jan Vondrak: The probabilistic method, 2008. Lecture notes at Charles University.

[55]   M. Minsky and S. Papert: Perceptrons. MIT Press, 1969.

[56]   Serge A. Plotkin, David B. Shmoys, and Éva Tardos: Fast approximation algorithm for fractional packing and covering problems. Math. Oper. Res., 20:257–301, 1995. Preliminary version in FOCS’91. [doi:10.1287/moor.20.2.257]

[57]   Prabhakar Raghavan: Probabilistic construction of deterministic algorithms: Approximating packing integer programs. J. Comput. System Sci., 37:130–143, 1988. Preliminary version in FOCS’86. [doi:10.1016/0022-0000(88)90003-7]

[58]   Prabhakar Raghavan and Clark D. Thompson: Randomized rounding: A technique for provably good algorithms and algorithmic proofs. Combinatorica, 7(4):365–374, 1987. [doi:10.1007/BF02579324]

[59]   Julia Robinson: An iterative method of solving a game. Annals of Mathematics, 54:296–301, 1951. [doi:10.2307/1969530]

[60]   Robert E. Schapire: The strength of weak learnability. Machine Learning, 5:197–227, 1990. [doi:10.1007/BF00116037]

[61]   Colin J. Thompson: Inequality with applications in statistical mechanics. J. Math. Phys., 6(11):1812–1823, 1965. [doi:10.1063/1.1704727]

[62]   Koji Tsuda, Gunnar Rätsch, and Manfred K. Warmuth: Matrix exponentiated gradient updates for on-line learning and Bregman projection. J. Machine Learning Research (JMLR), 6:995–1018, 2005. [JMLR PDF] .

[63]   Manfred K. Warmuth and Dima Kuzmin: Online variance minimization. Machine Learning, 87:1–32, 2012. Preliminary version in COLT’06. [doi:10.1007/s10994-011-5269-0]

[64]   Andrew C. Yao: Theory and applications of trapdoor functions (extended abstract). In Proc. 23rd FOCS, pp. 80–91. IEEE Comp. Soc. Press, 1982. [doi:10.1109/SFCS.1982.88]

[65]   Neal E. Young: Randomized rounding without solving the linear program. In Proc. 6th Ann. ACM-SIAM Symp. on Discrete Algorithms (SODA’95), pp. 170–178. ACM Press, 1995. [ACM DL].

[66]   Martin Zinkevich: Online convex programming and generalized infinitesimal gradient ascent. In Proc. 20th Int. Conf. on Machine Learning (ICML’03), pp. 928–936, 2003.