[1]   Donald Aingworth, Chandra Chekuri, Piotr Indyk, and Rajeev Motwani: Fast estimation of diameter and shortest paths (without matrix multiplication). SIAM J. Comput., 28(4):1167–1181, 1999. Preliminary version in SODA’96. [doi:10.1137/S0097539796303421]

[2]   Martin Albrecht, Gregory Bard, and William Hart: Algorithm 898: Efficient multiplication of dense matrices over GF(2). ACM Trans. Math. Softw., 37(1), 2010. [doi:10.1145/1644001.1644010]

[3]   Noga Alon, Richard A. Duke, Hanno Lefmann, Vojtech Rödl, and Raphael Yuster: The algorithmic aspects of the regularity lemma. J. Algorithms, 16(1):80–109, 1994. Preliminary version in FOCS’92. [doi:10.1006/jagm.1994.1005]

[4]   Noga Alon, Eldar Fischer, Michael Krivelevich, and Mario Szegedy: Efficient testing of large graphs. Combinatorica, 20(4):451–476, 2000. Preliminary version in FOCS’99. [doi:10.1007/s004930070001]

[5]   Noga Alon, Eldar Fischer, Ilan Newman, and Asaf Shapira: A combinatorial characterization of the testable graph properties: It’s all about regularity. SIAM J. Comput., 39(1):143–167, 2009. Preliminary version in STOC’06. [doi:10.1137/060667177]

[6]   Noga Alon and Assaf Naor: Approximating the cut-norm via Grothendieck’s inequality. SIAM J. Comput., 35(4):787–803, 2006. Preliminary version in STOC’04. [doi:10.1137/S0097539704441629]

[7]   Dana Angluin: The four Russians’ algorithm for Boolean matrix multiplication is optimal for its class. SIGACT News, 1:29–33, 1976. [doi:10.1145/1008591.1008593]

[8]   V. Z. Arlazarov, E. A. Dinic, M. A. Kronrod, and I. A. Faradzhev: On economical construction of the transitive closure of a directed graph. Soviet Mathematics Doklady, 11(5):1209–1210, 1970.

[9]   Michael D. Atkinson and Nicola Santoro: A practical algorithm for Boolean matrix multiplication. Inf. Process. Lett., 29:37–38, 1988. [doi:10.1016/0020-0190(88)90130-5]

[10]   Julien Basch, Sanjeev Khanna, and Rajeev Motwani: On diameter verification and Boolean matrix multiplication, 1995. Technical Report No. STAN-CS-95-1544, Department of Computer Science, Stanford University.

[11]   F. A. Behrend: On sets of integers which contain no three terms in arithmetic progression. Proc. Nat. Acad. Sci., 32(12):331–332, 1946.

[12]    Arnab Bhattacharyya, Victor Chen, Madhu Sudan, and Ning Xie: Testing linear-invariant non-linear properties. Theory of Computing, 7:75–99, 2011. Preliminary version in STACS’06. [doi:10.4086/toc.2011.v007a006]

[13]   Guy E. Blelloch, Virginia Vassilevska, and Ryan Williams: A new combinatorial approach for sparse graph problems. In Proc. 35th Internat. Colloq. on Automata, Languages and Programming (ICALP’08), pp. 108–120, 2008. [doi:10.1007/978-3-540-70575-8_10]

[14]   Avrim Blum: 2009. Personal communication.

[15]   Christian Borgs, Jennifer T. Chayes, László Lovász, Vera T. Sós, Balázs Szegedy, and Katalin Vesztergombi: Graph limits and parameter testing. In Proc. 38th STOC, pp. 261–270. ACM Press, 2006. [doi:10.1145/1132516.1132556]

[16]   Timothy M. Chan: More algorithms for all-pairs shortest paths in weighted graphs. In Proc. 39th STOC, pp. 590–598. ACM Press, 2007. [doi:10.1145/1250790.1250877]

[17]   Siddhartha Chatterjee, Alvin R. Lebeck, Praveen K. Patnala, and Mithuna Thottethodi: Recursive array layouts and fast matrix multiplication. IEEE Trans. on Parallel and Distributed Systems, 13:1105–1123, 2002. [doi:10.1109/TPDS.2002.1058095]

[18]   Henry Cohn, Robert D. Kleinberg, Balázs Szegedy, and Christopher Umans: Group-theoretic algorithms for matrix multiplication. In Proc. 46th FOCS, pp. 379–388. IEEE Comp. Soc. Press, 2005. [doi:10.1109/SFCS.2005.39]

[19]   Henry Cohn and Christopher Umans: A group-theoretic approach to fast matrix multiplication. In Proc. 44th FOCS, pp. 438–449. IEEE Comp. Soc. Press, 2003. [doi:10.1109/SFCS.2003.1238217]

[20]   Amin Coja-Oghlan, Colin Cooper, and Alan M. Frieze: An efficient sparse regularity concept. SIAM J. Discrete Math., 23(4):2000–2034, 2010. [doi:10.1137/080730160]

[21]   Dorit Dor, Shay Halperin, and Uri Zwick: All-pairs almost shortest paths. SIAM J. Comput., 29(5):1740–1759, 2000. Preliminary version in FOCS’96. [doi:10.1137/S0097539797327908]

[22]   Richard A. Duke, Hanno Lefmann, and Vojtech Rödl: A fast approximation algorithm for computing the frequencies of subgraphs in a given graph. SIAM J. Comput., 24(3):598–620, 1995. [doi:10.1137/S0097539793247634]

[23]   Michael Elkin: An improved construction of progression-free sets. In Proc. 21st Ann. ACM-SIAM Symp. on Discrete Algorithms (SODA’10), pp. 886–905, 2010.

[24]    Tomás Feder and Rajeev Motwani: Clique partitions, graph compression and speeding-up algorithms. J. Comput. System Sci., 51(2):261–272, 1995. Preliminary version in STOC’91. [doi:10.1006/jcss.1995.1065]

[25]   Michael J. Fischer and Albert R. Meyer: Boolean matrix multiplication and transitive closure. In Proc. 12th FOCS (SWAT’71), pp. 129–131. IEEE Comp. Soc. Press, 1971. [doi:10.1109/SWAT.1971.4]

[26]   Jacob Fox: A new proof of the graph removal lemma. Ann. of Math., 174(1):561–579, 2011. [doi:10.4007/annals.2011.174.1.17]

[27]   Alan Frieze and Ravi Kannan: A simple algorithm for constructing Szemerédi’s regularity partition. Electr. J. Comb., 6, 1999.

[28]   Alan M. Frieze and Ravi Kannan: The Regularity Lemma and approximation schemes for dense problems. In Proc. 37th FOCS, pp. 12–20. IEEE Comp. Soc. Press, 1996. [doi:10.1109/SFCS.1996.548459]

[29]   Alan M. Frieze and Ravi Kannan: Quick approximation to matrices and applications. Combinatorica, 19(2):175–220, 1999. [doi:10.1007/s004930050052]

[30]   Anka Gajentaan and Mark H. Overmars: On a class of o(n²) problems in computational geometry. Computational Geometry, 5:165–185, 1995. [doi:10.1016/0925-7721(95)00022-2]

[31]   Zvi Galil and Oded Margalit: All pairs shortest distances for graphs with small integer length edges. Inform. and Comput., 134:103–139, 1997. [doi:10.1006/inco.1997.2620]

[32]   W. T. Gowers: Lower bounds of tower type for Szemerédi’s uniformity lemma. Geom. and Funct. Anal., 7:322–337, 1997. [doi:10.1007/PL00001621]

[33]   Ben Green: A Szemerédi-type regularity lemma in abelian groups. Geom. and Funct. Anal., 15:340–376, 2005. [doi:10.1007/s00039-005-0509-8]

[34]   András Hajnal, Wolfgang Maass, and György Turán: On the communication complexity of graph properties. In Proc. 20th STOC, pp. 186–191. ACM Press, 1988. [doi:10.1145/62212.62228]

[35]   Alon Itai and Michael Rodeh: Finding a minimum circuit in a graph. SIAM J. Comput., 7(4):413–423, 1978. [doi:10.1137/0207033]

[36]   Y. Kohayakawa: Szemerédi’s regularity lemma for sparse graphs. In F. Cucker and M. Shub, editors, Foundations of Computational Mathematics, pp. 216–230. Springer, 1997.

[37]   Yoshiharu Kohayakawa, Vojtech Rödl, and Lubos Thoma: An optimal algorithm for checking regularity. SIAM J. Comput., 32(5):1210–1235, 2003. [doi:10.1137/S0097539702408223]

[38]   János Komlós and Miklós Simonovits: Szemerédi’s Regularity Lemma and its applications in graph theory. In Combinatorics, Paul Erd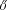s is Eighty, (D. Miklós et. al, eds.), Bolyai Society Mathematical Studies, volume 2, pp. 295–352, 1996.

[39]   Daniel Král, Oriol Serra, and Lluís Vena: A removal lemma for systems of linear equations over finite fields. Israel J. Math., 187(1):193–207, 2012. [doi:10.1007/s11856-011-0080-y]

[40]   Lillian Lee: Fast context-free grammar parsing requires fast Boolean matrix multiplication. J. ACM, 49:1–15, 2002. [doi:10.1145/505241.505242]

[41]   Andrzej Lingas: A geometric approach to Boolean matrix multiplication. In Proc. 13th Int. Symp. on Algorithms and Computation (ISAAC’02), pp. 501–510, 2002. [doi:10.1007/3-540-36136-7_44]

[42]   László Lovász and Balázs Szegedy: Szemerédi’s theorem for the analyst. Geom. and Funct. Anal., 17(1):252–270, 2007. [doi:10.1007/s00039-007-0599-6]

[43]   J. W. Moon and L. Moser: A matrix reduction problem. Mathematics of Computation, 20:328–330, 1966. [doi:10.1090/S0025-5718-66-99935-2]

[44]   Patrick E. O’Neil and Elizabeth J. O’Neil: A fast expected time algorithm for Boolean matrix multiplication and transitive closure matrices. Inf. Control, 22:132–138, 1973. [doi:10.1016/S0019-9958(73)90228-3]

[45]   Victor Y. Pan: How to Multiply Matrices Faster. Volume 179 of Lecture Notes in Computer Science. Springer, 1984.

[46]   Mihai Patrascu: Towards polynomial lower bounds for dynamic problems. In Proc. 42nd STOC, pp. 603–610. ACM Press, 2010. [doi:10.1145/1806689.1806772]

[47]   Liam Roditty and Uri Zwick: On dynamic shortest paths problems. Algorithmica, 61(2):389–401, 2010. Preliminary version in 12th Europ. Symp. Algor. (ESA’04). [doi:10.1007/s00453-010-9401-5]

[48]   Vojtěch Rödl and Mathias Schacht: Property testing in hypergraphs and the removal lemma. In Proc. 39th STOC, pp. 488–495. ACM Press, 2007. [doi:10.1145/1250790.1250862]

[49]   I. Z. Ruzsa and E. Szemerédi: Triple systems with no six points carrying three triangles. Colloquia Mathematica Societatis János Bolyai, 18:939–945, 1978.

[50]   Wojciech Rytter: Fast recognition of pushdown automaton and context-free languages. Inf. Control, 67:12–22, 1985. Preliminary version in MFCS’84. [doi:10.1016/S0019-9958(85)80024-3]

[51]   John E. Savage: An algorithm for the computation of linear forms. SIAM J. Comput., 3:150–158, 1974. [doi:10.1137/0203011]

[52]   C.-P. Schnorr and C. R. Subramanian: Almost optimal (on the average) combinatorial algorithms for Boolean matrix product witnesses, computing the diameter. In Proc. 2nd Intern. Workshop Random. and Approx. Tech. Comput. Sci. (RANDOM’98), pp. 218–231, 1998. [doi:10.1007/3-540-49543-6_18]

[53]   Raimund Seidel: On the all-pairs-shortest-path problem in unweighted undirected graphs. J. Comput. System Sci., 51(3):400–403, 1995. [doi:10.1006/jcss.1995.1078]

[54]   Asaf Shapira: Green’s conjecture and testing linear-invariant properties. In Proc. 41st STOC, pp. 159–166. ACM Press, 2009. [doi:10.1145/1536414.1536438]

[55]   Avi Shoshan and Uri Zwick: All pairs shortest paths in undirected graphs with integer weights. In Proc. 40th FOCS, pp. 605–614. IEEE Comp. Soc. Press, 1999. [doi:10.1109/SFFCS.1999.814635]

[56]   Volker Strassen: Gaussian elimination is not optimal. Numerische Mathematik, 13(4):354–356, 1969. [doi:10.1007/BF02165411]

[57]   Endre Szemerédi: Regular partitions of graphs. In Proc. Colloque Inter. CNRS (J. C. Bermond, J. C. Fournier, M. Las Vergnas and D. Sotteau, eds.), pp. 399–401, 1978.

[58]   Luca Trevisan: Additive combinatorics and theoretical computer science. In SIGACT News Complexity Column 63, 2009.

[59]   Leslie G. Valiant: General context-free recognition in less than cubic time. J. Comput. System Sci., 10(2):308–315, 1975. [doi:10.1016/S0022-0000(75)80046-8]

[60]   Virginia Vassilevska Williams: Multiplying matrices faster than Coppersmith-Winograd. In Proc. 44th STOC, 2012. To appear.

[61]   Virginia Vassilevska Williams and Ryan Williams: Subcubic equivalences between path, matrix, and triangle problems. In Proc. 51st FOCS, pp. 645–654. IEEE Comp. Soc. Press, 2010. [doi:10.1109/FOCS.2010.67]

[62]   Ryan Williams: Matrix-vector multiplication in sub-quadratic time (some preprocessing required). In Proc. 18th Ann. ACM-SIAM Symp. on Discrete Algorithms (SODA’07), pp. 995–1001. ACM Press, 2007.