Separating Deterministic from Randomized Multiparty Communication Complexity
by Paul Beame, Matei David, Toniann Pitassi, and Philipp Woelfel
Theory of Computing, Volume 6(9), pp. 201-225, 2010
Bibliography with links to cited articles
[1] László Babai, Péter Frankl, and János Simon: Complexity classes in communication complexity theory (preliminary version). In Proc. 27th FOCS, pp. 337–347. IEEE Comput. Soc. Press, 1986. [doi:10.1109/SFCS.1986.15]
[2] László Babai, Anna Gál, Peter Kimmel, and Satyanarayana Lokam: Communication complexity of simultaneous messages. SIAM J. Comput., 33(1):137–166, 2004. [doi:10.1137/S0097539700375944]
[3] László Babai, Thomas Hayes, and Peter Kimmel: The cost of the missing bit: Communication complexity with help. Combinatorica, 21(4):455–488, 2001.
[4] László Babai, Noam Nisan, and Márió Szegedy: Multiparty protocols, pseudorandom generators for logspace, and time-space trade-offs. J. Comput. System Sci., 45(2):204–232, 1992. [doi:10.1016/0022-0000(92)90047-M]
[5] Paul Beame, Matei David, Toniann Pitassi, and Philipp Woelfel: Separating deterministic from nondeterministic NOF multiparty communication complexity. In Proc. 34th Intern. Colloq. Autom. Lang. Program. (ICALP), volume 4596 of LNCS, pp. 134–145. Springer, 2007.
[6] Paul Beame, Trinh Huynh, and Toniann Pitassi: Hardness amplification in proof complexity. In Proc. 42nd STOC, pp. 87–96. ACM Press, 2010. [doi:10.1145/1806689.1806703]
[7] Paul Beame and Dang-Trinh Huynh-Ngoc: Multiparty communication complexity and threshold circuit size of AC0. In Proc. 50th FOCS, pp. 53–62. IEEE Comput. Soc. Press, 2009. [doi:10.1109/FSCS.2009.12]
[8] Paul Beame, Toniann Pitassi, and Nathan Segerlind: Lower bounds for Lovász–Schrijver systems and beyond follow from multiparty communication complexity. SIAM J. Comput., 37(3):845–869, 2007. [doi:10.1137/060654645]
[9] Richard Beigel, William Gasarch, and James Glenn: The multiparty communication complexity of Exact-T: Improved bounds and new problems. In Proc. 31st. Intern. Symp. Math. Found. Comput. Sci. (MFCS), volume 4162 of LNCS, pp. 146–156. Springer, 2006. [doi:10.1007/11821069_13]
[10] Richard Beigel and Jun Tarui: On ACC. Comput. Complexity, 4(4):350–366, 1994. [doi:10.1007/BF01263423]
[11] J. Lawrence Carter and Mark N. Wegman: Universal classes of hash functions. J. Comput. System Sci., 18(2):143–154, 1979. [doi:10.1016/0022-0000(79)90044-8]
[12] Ashok K. Chandra, Merrick L. Furst, and Richard J. Lipton: Multi-party protocols. In Proc. 15th STOC, pp. 94–99. ACM Press, 1983. [doi:10.1145/800061.808737]
[13] Arkadev Chattopadhyay and Anil Ada: Multiparty communication complexity of disjointness. Technical Report TR08-002, Electron. Colloq. on Comput. Complexity (ECCC), 2008.
[14] Matei David, Toniann Pitassi, and Emanuele Viola: Improved separations between nondeterministic and randomized multiparty communication. ACM Trans. Comput. Log., 1(2):1–20, 2009. [doi:10.1145/1595391.1595392]
[15] Dmitry Gavinsky and Alexander A. Sherstov: A separation of NP and coNP in multiparty communication complexity. Theory of Computing, 6:227–245, 2010. [doi:10.4086/toc2010.v006a010]
[16] Johan Håstad and Mikael Goldmann: On the power of small-depth threshold circuits. Comput. Complexity, 1(2):113–129, 1991. [doi:10.1007/BF01272517]
[17] Hartmut Klauck: Lower bounds for quantum communication complexity. SIAM J. Comput., 37(1):20–46, 2007. [doi:10.1137/S0097539702405620]
[18] Eyal Kushilevitz and Noam Nisan: Communication Complexity. Cambridge University Press, 1997.
[19] Troy Lee and Adi Shraibman: Disjointness is hard in the multi-party number-on-the-forehead model. In Proc. 23rd Comput. Complex. Conf. (CCC), pp. 81–91. IEEE Comput. Soc. Press, 2008. [doi:10.1109/CCC.2008.29]
[20] Yishay Mansour, Noam Nisan, and Prasoon Tiwari: The computational complexity of universal hashing. Theoret. Comput. Sci., 107(1):121–133, 1993. [doi:10.1016/0304-3975(93)90257-T]
[21] Ilan Newman: Private vs. common random bits in communication complexity. Inform. Process. Lett., 39(2):67–71, 1991. [doi:10.1016/0020-0190(91)90157-D]
[22] Noam Nisan: The communication complexity of threshold gates. In
Combinatorics, Paul Erd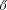 s is Eighty, number 1 in Bolyai Society
Mathematical Studies, pp. 301–315. J. Bolyai Math. Soc., Budapest, 1993.
s is Eighty, number 1 in Bolyai Society
Mathematical Studies, pp. 301–315. J. Bolyai Math. Soc., Budapest, 1993.
[23] Noam Nisan and Avi Wigderson: Rounds in communication complexity revisited. SIAM J. Comput., 22(1):211–219, 1993. [doi:10.1137/0222016]
[24] A. A. Razborov: Quantum communication complexity of symmetric predicates. Izv. Math., 67(1):145–159, 2003. [doi:10.1070/IM2003v067n01ABEH000422]
[25] Alexander A. Sherstov: Communication lower bounds using dual polynomials. Bull. Eur. Assoc. Theor. Comput. Sci. EATCS, 95:59–93, 2008.
[26] Andrew Chi-Chih Yao: Some complexity questions related to distributive computing (preliminary report). In Proc. 11th STOC, pp. 209–213. ACM Press, 1979. [doi:10.1145/800135.804414]
[27] Andrew Chi-Chih Yao: On ACC and threshold circuits. In Proc. 31st FOCS, volume 2, pp. 619–627, 1990. [doi:10.1109/FSCS.1990.89583]
