[1]   Manindra Agrawal and V. Vinay: Arithmetic circuits: A chasm at depth four. In Proc. 49th FOCS, pp. 67–75. IEEE Comp. Soc., 2008. [doi:10.1109/FOCS.2008.32].

[2]   M. Ajtai: Σ₁¹-formulae on finite structures. Ann. Pure Appl. Logic, 24:1–48, 1983. [doi:10.1016/0168-0072(83)90038-6].

[3]   Michael Alekhnovich, Eli Ben-Sasson, Alexander A. Razborov, and Avi Wigderson: Pseudorandom generators in propositional proof complexity. SIAM J. Comput., 34(1):67–88, 2004. A preliminary version appeared in FOCS 2000. [doi:10.1137/S0097539701389944].

[4]   Michael Alekhnovich and Alexander A. Razborov: Lower bounds for the polynomial calculus: Non-binomial case. Proc. Steklov Inst. Math., 242:18–35, 2003. A preliminary version appeared in FOCS 2001. [doi:10.1109/SFCS.2001.959893].

[5]   Walter Baur and Volker Strassen: The complexity of partial derivatives. Theoret. Comput. Sci., 22(3):317–330, 1983. [doi:10.1016/0304-3975(83)90110-X].

[6]   Peter Bürgisser: Completeness and Reduction in Algebraic Complexity Theory. Springer, Berlin, 2000.

[7]   Peter Bürgisser, Michel Clausen, and Mohammad A. Shokrollahi: Algebraic Complexity Theory. Springer, Berlin, 1997.

[8]   Danny Dolev, Cynthia Dwork, Nicholas Pippenger, and Avi Wigderson: Superconcentrators, generalizers and generalized connectors with limited depth. In Proc. 15th STOC, pp. 42–51. ACM, 1983. [doi:10.1145/800061.808731].

[9]   Merrick L. Furst, James B. Saxe, and Michael Sipser: Parity, circuits, and the polynomial-time hierarchy. Theory Comput. Syst., 17(1):13–27, 1984. A preliminary version appeared in FOCS 1981. [doi:10.1007/BF01744431].

[10]   Joachim von zur Gathen: Feasible arithmetic computations: Valiant’s hypothesis. J. Symbolic Comput., 4(2):137–172, 1987. [doi:10.1016/S0747-7171(87)80063-9].

[11]   Joachim von zur Gathen: Algebraic complexity theory. Ann. Rev. Comput. Sci., 3:317–347, 1988. [doi:10.1146/annurev.cs.03.060188.001533].

[12]   Dima Grigoriev and Marek Karpinski: An exponential lower bound for depth 3 arithmetic circuits. In Proc. 30th STOC, pp. 577–582, 1998. [doi:10.1145/276698.276872].

[13]   D. Grigoriev and A. Razborov: Exponential lower bounds for depth 3 arithmetic circuits in algebras of functions over finite fields. Appl. Algebra Engrg. Comm. Comput., 10(6):465–487, 2000. A preliminary version appeared in FOCS 1998. [doi:10.1007/s002009900021].

[14]   J. Håstad: Almost optimal lower bounds for small depth circuits. Adv. Comput. Res., 5:143–170, 1989. A preliminary version appeared in STOC 1986. [doi:10.1145/12130.12132].

[15]   Valentine Kabanets and Russell Impagliazzo: Derandomizing polynomial identity tests means proving circuit lower bounds. Comput. Complexity, 13(1–2):1–46, 2004. A preliminary version appeared in STOC 2003. [doi:10.1007/s00037-004-0182-6].

[16]   Richard J. Lipton: Polynomials with 0-1 coefficients that are hard to evaluate. SIAM J. Comput., 7(1):61–69, 1978. A preliminary version appeared in FOCS 1975. [doi:10.1137/0207004].

[17]   Satyanarayana V. Lokam: Spectral methods for matrix rigidity with applications to size-depth tradeoffs and communication complexity. J. Comput. System Sci., 63:449–473, 2001. A preliminary version appeared in FOCS 1995. [doi:10.1006/jcss.2001.1786].

[18]   Jacques Morgenstern: How to compute fast a function and all its derivatives: A variation on the theorem of Baur-Strassen. ACM SIGACT News, 16:60–62, 1985. [doi:10.1145/382242.382836].

[19]   Noam Nisan: Lower bounds for non-commutative computation. In Proc. 13th STOC, pp. 410–418. ACM, 1991. [doi:10.1145/103418.103462].

[20]   Noam Nisan and Avi Wigderson: On the complexity of bilinear forms. In Proc. 27th STOC, pp. 723–732. ACM, 1995. [doi:10.1145/225058.225290].

[21]   P. Pudlák: Communication in bounded depth circuits. Combinatorica, 14:203–216, 1994. [doi:10.1007/BF01215351].

[22]   Pavel Pudlák: A note on the use of determinant for proving lower bounds on the size of linear circuits. Inform. Process. Lett., 74:197–201, 2000. [doi:10.1016/S0020-0190(00)00058-2].

[23]   Ran Raz: On the complexity of matrix product. SIAM J. Comput., 32(5):1356–1369, 2003. A preliminary version appeared in STOC 2002. [doi:10.1137/S0097539702402147].

[24]   Ran Raz: Separation of multilinear circuit and formula size. Theory Comput., 2(6):121–135, 2006. A preliminary version appeared in FOCS 2004 with the title “Multilinear-NC₁ 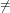Multilinear-NC₂”. [doi:10.4086/toc.2006.v002a006].

[25]   Ran Raz: Multi-linear formulas for permanent and determinant are of super-polynomial size. J. ACM, 56, 2009. A preliminary version appeared in STOC 2004. [doi:10.1145/1502793.1502797].

[26]   Ran Raz: Tensor-rank and lower bounds for arithmetic formulas. In Proc. 42nd STOC, pp. 659–666. ACM, 2010. [doi:10.1145/1806689.1806780].

[27]   Ran Raz and Amir Shpilka: Lower bounds for matrix product in bounded depth circuits with arbitrary gates. SIAM J. Comput., 32(2):488–513, 2003. A preliminary version appeared in STOC 2001. [doi:10.1137/S009753970138462X].

[28]   Ran Raz and Amir Yehudayoff: Multilinear formulas, maximal-partition discrepancy and mixed-sources extractors. J. Comput. System Sci., 2010. A preliminary version appeared in FOCS 2008. [doi:10.1016/j.jcss.2010.06.013].

[29]   A. A. Razborov: Lower bounds on the size of bounded-depth networks over a complete basis with logical addition (in Russian). Mat. Zametki, 41(4):598–607, 1987. An English translation appeared in Mathematical Notes of the Academy of Sci. of the USSR 41(4) (1987) 333–338.

[30]   A. A. Razborov: Bounded arithmetic and lower bounds in Boolean complexity. In Feasible Mathematics II, volume 13 of Progr. Comput. Sci. Appl. Logic, pp. 344–386. Birkhäuser, 1995.

[31]   Victor Shoup and Roman Smolensky: Lower bounds for polynomial evaluation and interpolation problems. In Proc. 32nd FOCS, pp. 378–383. IEEE Comp. Soc., 1991. [doi:10.1109/SFCS.1991.185394].

[32]   A. Shpilka and A. Wigderson: Depth-3 arithmetic circuits over fields of characteristic zero. Comput. Complexity, 10(1):1–27, 2001. A preliminary version appeared in Conference on Computational Complexity 1999. [doi:10.1007/PL00001609].

[33]   R. Smolensky: Algebraic methods in the theory of lower bounds for Boolean circuit complexity. In Proc. 19th STOC, pp. 77–82. ACM, 1987. [doi:10.1145/28395.28404].

[34]   Volker Strassen: Polynomials with rational coefficients which are hard to compute. SIAM J. Comput., 3(2):128–149, 1974. [doi:10.1137/0203010].

[35]   Volker Strassen: Die Berechnungskomplexität der symbolischen Differentiation von Interpolationspolynomen. Theoret. Comput. Sci., 1(1):21–25, 1975. [doi:10.1016/0304-3975(75)90010-9].

[36]   L. G. Valiant: Completeness classes in algebra. In Proc. 11th STOC, pp. 249–261, 1979. [doi:10.1145/800135.804419].

[37]   L. G. Valiant, S. Skyum, S. Berkowitz, and C. Rackoff: Fast parallel computation of polynomials using few processors. SIAM J. Comput., 12(4):641–644, 1983. [doi:10.1137/0212043].

[38]   Andrew Chi-Chih Yao: Separating the polynomial-time hierarchy by oracles. In Proc. 26th FOCS, pp. 1–10. IEEE Comp. Soc., 1985. [doi:10.1109/SFCS.1985.49].