[1]   Amit Agarwal, Moses Charikar, Konstantin Makarychev, and Yury Makarychev: O(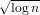) approximation algorithms for Min-Uncut, Min-2CNF-Deletion, and directed cut problems. In Proc. 37th STOC, pp. 573–581. ACM Press, 2005. [doi:10.1145/1060590.1060675].

[2]   Noga Alon, Konstantin Makarychev, Yury Makarychev, and Assaf Naor: Quadratic forms on graphs. Invent. Math., 163(3), 2006. [doi:10.1007/s00222-005-0465-9].

[3]   Noga Alon and Assaf Naor: Approximating the Cut-Norm via Grothendieck’s inequality. SIAM J. Comput., 35(4):787–803, 2006. [doi:10.1137/S0097539704441629].

[4]   Noga Alon, Benny Sudakov, and Uri Zwick: Constructing worst case instances for semidefinite programming based approximation algorithms. SIAM J. Discrete Math., 15(1):58–72, 2002. [doi:10.1137/S0895480100379713].

[5]   Sanjeev Arora, Eli Berger, Elad Hazan, Guy Kindler, and Muli Safra: On non-approximability for quadratic programs. In Proc. 46th FOCS, pp. 206–215. IEEE Comp. Soc. Press, 2005. [doi:10.1109/SFCS.2005.57].

[6]   Sanjeev Arora, Satish Rao, and Umesh Vazirani: Expander flows, geometric embeddings and graph partitioning. In Proc. 36th STOC, pp. 222–231. ACM Press, 2004. [doi:10.1145/1007352.1007355].

[7]   Nikhil Bansal, Avrim Blum, and Shuchi Chawla: Correlation clustering. Machine Learning, 56(1-3):89–113, 2004. [doi:10.1023/B:MACH.0000033116.57574.95].

[8]   Mihir Bellare, Oded Goldreich, and Madhu Sudan: Free bits, PCPs, and nonapproximability—towards tight results. SIAM J. Comput., 27(3):804–915, 1998. [doi:10.1137/S0097539796302531].

[9]   Algimantas Bikelis: Estimates of the remainder in the Central Limit Theorem. Litovsk. Mat. Sb., 6(3):323–346, 1966. In Russian.

[10]   Christer Borell: Geometric bounds on the Ornstein-Uhlenbeck velocity process. Z. Wahrsch. Verw. Gebiete, 70(1):1–13, 1985. [doi:10.1007/BF00532234].

[11]   Moses Charikar, Konstantin Makarychev, and Yury Makarychev: Near-optimal algorithms for unique games. In Proc. 38th STOC, pp. 205–214. ACM Press, 2006. [doi:10.1145/1132516.1132547].

[12]   Moses Charikar and Anthony Wirth: Maximizing quadratic programs: Extending Grothendieck’s inequality. In Proc. 45th FOCS, pp. 54–60. IEEE Comp. Soc. Press, 2004. [doi:10.1109/FOCS.2004.39].

[13]   Shuchi Chawla, Robert Krauthgamer, Ravi Kumar, Yuval Rabani, and D. Sivakumar: On the hardness of approximating Multicut and Sparsest-Cut. Comput. Complexity, 15(2):94–114, 2006. [doi:10.1007/s00037-006-0210-9].

[14]   Herman Chernoff: A measure of asymptotic efficiency for tests of a hypothesis based on the sum of observations. Annals of Mathematical Statistics, 23(4), 1952. [doi:10.1214/aoms/1177729330].

[15]   Harald Cramér: Sur un nouveau théroème-limite de la théorie des probabilités. Actualités Scientifiques et Industrielles, 736, 1938.

[16]   Pierluigi Crescenzi, Riccardo Silvestri, and Luca Trevisan: On weighted vs. unweighted versions of combinatorial optimization problems. Inform. and Comput., 167(1):10–26, 2001. [doi:10.1006/inco.2000.3011].

[17]   Alexander Davie: Lower bound for K_G. Unpublished, 1984.

[18]   Irit Dinur, Elchanan Mossel, and Oded Regev: Conditional hardness for approximate coloring. In Proc. 38th STOC, pp. 344–353. ACM Press, 2006. [doi:10.1145/1132516.1132567].

[19]   Uriel Feige and Michael Langberg: The RPR² rounding technique for semidefinite programs. J. Algorithms, 60(1):1–23, 2006. [doi:10.1016/j.jalgor.2004.11.003].

[20]   Michel Goemans and David Williamson: Improved approximation algorithms for maximum cut and satisfiability problems using semidefinite programming. J. ACM, 42:1115–1145, 1995. [doi:10.1145/227683.227684].

[21]   Ben Green: A Szemerédi-type regularity lemma in abelian groups, with applications. Geom. Funct. Anal., 15(2):340–376, 2005. [doi:10.1007/s00039-005-0509-8].

[22]   Alexandre Grothendieck: Résumé de la théorie métrique des produits tensoriels topologiques. Bol. Soc. Mat. Sao Paulo, 8:1–79, 1953.

[23]   Uffe Haagerup: A new upper bound for the complex Grothendieck constant. Israel J. Math., 60(2):199–224, 1987. [doi:10.1007/BF02790792].

[24]   Johan Håstad: Some optimal inapproximability results. J. ACM, 48(4):798–859, 2001. [doi:10.1145/502090.502098].

[25]   Johan Håstad and Srinivasan Venkatesh: On the advantage over a random assignment. Random Structures Algorithms, 25(2):117–149, 2004. [doi:10.1002/rsa.20031].

[26]   George Karakostas: A better approximation ratio for the Vertex Cover problem. In Proc. 32nd Internat. Conf. on Automata, Languages, and Programming (ICALP), volume 3580 of Lecture Notes in Computer Science, pp. 1043–1050. Springer, 2005. [doi:10.1007/11523468_84].

[27]   Subhash Khot: On the power of unique 2-prover 1-round games. In Proc. 34th STOC, pp. 767–775. ACM Press, 2002. [doi:10.1145/509907.510017].

[28]   Subhash Khot, Guy Kindler, Elchanan Mossel, and Ryan O’Donnell: Optimal inapproximability results for MAX-CUT and other 2-variable CSPs? SIAM J. Comput., 37(1):319–357, 2007. [doi:10.1137/S0097539705447372].

[29]   Subhash Khot and Assaf Naor: Nonembeddability theorems via Fourier analysis. Math. Ann., 334(4):821–852, 2006. [doi:10.1007/s00208-005-0745-0].

[30]   Subhash Khot and Ryan O’Donnell: SDP gaps and UGC-hardness for MaxCutGain. In Proc. 47th FOCS, pp. 217–226. IEEE Comp. Soc. Press, 2006. [doi:10.1109/FOCS.2006.67].

[31]   Subhash Khot and Oded Regev: Vertex Cover might be hard to approximate to within 2 - ε. In Proc. 18th Conf. on Computational Complexity (CCC), pp. 379–386. IEEE Comp. Soc. Press, 2003.

[32]   Subhash Khot and Nisheeth Vishnoi: The Unique Games Conjecture, integrality gap for cut problems and embeddability of negative type metrics into ℓ₁. In Proc. 46th FOCS, pp. 53–62. IEEE Comp. Soc. Press, 2005. [doi:10.1109/SFCS.2005.74].

[33]   Robert Krauthgamer and Yuval Rabani: Improved lower bounds for embeddings into L₁. In Proc. 17th Symp. on Discrete Algorithms (SODA), pp. 1010–1017. ACM Press, 2006. [doi:10.1145/1109557.1109669].

[34]   Jean-Louis Krivine: Sur la constante de Grothendieck. Comptes Rendus Acad. Sci. Paris Sér. A-B, 284:445–446, 1977.

[35]   Michel Ledoux and Michel Talagrand: Probability in Banach Spaces. Springer, 1991.

[36]   Alexandre Megretski: Relaxations of quadratic programs in operator theory and system analysis. In Systems, Approximation, Singular Integral Operators, and Related Topics: International Workshop on Operator Theory and Applications. Birkhauser, 2001.

[37]   Elchanan Mossel, Ryan O’Donnell, and Krzysztof Oleszkiewicz: Noise stability of functions with low influences: Invariance and optimality. In Proc. 46th FOCS, pp. 21–30. IEEE Comp. Soc. Press, 2005. To appear, Annals of Mathematics. [doi:10.1109/SFCS.2005.53].

[38]   Arkadi Nemirovski, Cornelis Roos, and Tamás Terlaky: On maximization of quadratic form over intersection of ellipsoids with common center. Math. Program., 86(3):463–473, 1999. [doi:10.1007/s101070050100].

[39]   Yurii Nesterov: Global quadratic optimization via conic relaxation, pp. 363–384. Kluwer Academic Publishers, 2000.

[40]   Ryan O’Donnell and Yi Wu: An optimal SDP algorithm for Max-Cut, and equally optimal Long Code tests. In Proc. 40th STOC, pp. 335–344. ACM Press, 2008. [doi:10.1145/1374376.1374425].

[41]   Prasad Raghavendra: Optimal algorithms and inapproximability results for every CSP? In Proc. 40th STOC, pp. 245–254. ACM Press, 2008. [doi:10.1145/1374376.1374414].

[42]   Prasad Raghavendra and David Steurer: Towards computing the Grothendieck constant. In Proc. 19th Symposium on Discrete Algorithms (SODA), pp. 525–534. ACM Press, 2009.

[43]   James Reeds: A new lower bound on the real Grothendieck constant. Manuscript (http://www.dtc.umn.edu/~reedsj/bound2.dvi), 1991.

[44]   Luca Trevisan, Gregory Sorkin, Madhu Sudan, and David Williamson: Gadgets, approximation, and linear programming. SIAM J. Comput., 29(6):2074–2097, 2000. [doi:10.1137/S0097539797328847].

[45]   Uri Zwick: Outward rotations: A tool for rounding solutions of semidefinite programming relaxations, with applications to MAX CUT and other problems. In Proc. 31st STOC, pp. 679–687. ACM Press, 1999. [doi:10.1145/301250.301431].