



Next: Specialized Routines
Up: The script sdp.m
Previous: Invoking sdp.m or
The following output parameters are provided by both sdp.m
(as variables in the Matlab workspace) and fsdp.m (as
return values):
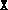 ,
, 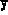 ,
, 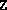
- The final values of the variables X, y and
Z. If
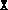 and
and 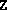 have multiple blocks, they are stored using
Matlab's sparse format. If they have only one block, then they are
always full.
have multiple blocks, they are stored using
Matlab's sparse format. If they have only one block, then they are
always full. 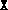 and
and 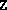 are numerically positive semidefinite in
the sense that Matlab's chol function does not encounter
negative pivots when applied to them.
are numerically positive semidefinite in
the sense that Matlab's chol function does not encounter
negative pivots when applied to them.
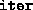
- The number of iterations taken by the algorithm.
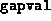
- A vector of length
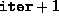 , with entries equal to the
value of
, with entries equal to the
value of 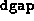 (
(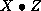 ) as a function of the iteration count.
The first entry in the
) as a function of the iteration count.
The first entry in the 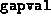 array is the value of
array is the value of 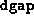 corresponding to the initial point provided.
corresponding to the initial point provided.

- A matrix with two columns and
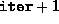 rows, whose
entries are the values of the primal and the dual objectives in the
first and the second columns respectively, as a function of the
iteration count.
rows, whose
entries are the values of the primal and the dual objectives in the
first and the second columns respectively, as a function of the
iteration count.
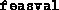
- A matrix with two columns and
 rows, whose
entries are the values of
rows, whose
entries are the values of  and
and 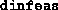 in the first and
the second columns respectively, as a function of the iteration count.
in the first and
the second columns respectively, as a function of the iteration count.
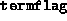
- This is the termination flag returned by
fsdp.m, with the following meaning:

- Successful termination: both the absolute and
relative tolerances were satisfied.

- The new primal iterate
 is numerically
indefinite, i.e. chol(X) encountered a negative pivot. This
would not occur in exact arithmetic. The algorithm terminates,
returning the current iterate
is numerically
indefinite, i.e. chol(X) encountered a negative pivot. This
would not occur in exact arithmetic. The algorithm terminates,
returning the current iterate 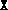 (which is positive semidefinite).
This is normal, and usually means the problem is essentially solved
but the termination criteria were too stringent. (If
(which is positive semidefinite).
This is normal, and usually means the problem is essentially solved
but the termination criteria were too stringent. (If 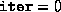 ,
this means that the initial
,
this means that the initial 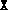 provided was not positive
semidefinite. This is easily remedied by adding a positive multiple
of the identity to
provided was not positive
semidefinite. This is easily remedied by adding a positive multiple
of the identity to 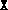 .)
.)

- The new dual iterate
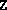 is numerically
indefinite, i.e. chol(Z) encountered a negative pivot. This
would not occur in exact arithmetic. The algorithm terminates,
returning the current iterate
is numerically
indefinite, i.e. chol(Z) encountered a negative pivot. This
would not occur in exact arithmetic. The algorithm terminates,
returning the current iterate 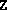 (which is positive semidefinite).
This termination flag is also used if chol finds that the new
iterate
(which is positive semidefinite).
This termination flag is also used if chol finds that the new
iterate 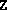 is numerically positive semidefinite, but the routine
blkeig finds that it has a zero (or negative) eigenvalue, in
which case the algorithm returns the new iterate, and then
terminates.
is numerically positive semidefinite, but the routine
blkeig finds that it has a zero (or negative) eigenvalue, in
which case the algorithm returns the new iterate, and then
terminates. Both cases are normal,
and they usually mean that the problem is essentially solved but that
the termination criteria were too stringent. (If
Both cases are normal,
and they usually mean that the problem is essentially solved but that
the termination criteria were too stringent. (If 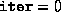 , this
means that the initial
, this
means that the initial 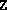 provided was not positive semidefinite.
This is easily remedied by adding a positive multiple of the identity
to
provided was not positive semidefinite.
This is easily remedied by adding a positive multiple of the identity
to 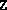 .)
.)

- Termination occurred because the Schur
complement was numerically singular, i.e. the Matlab routine
lu generates a zero pivot, making the XZ+ZX direction
undefined. The most likely explanation is that the matrix
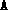 was
rank deficient. The routine preproc.m can help in detecting
inconsistent constraints and in the elimination of redundant
constraints (see Section 5). Otherwise, this is a
rare situation which might occur close to the solution, if the
termination criteria are too stringent.
was
rank deficient. The routine preproc.m can help in detecting
inconsistent constraints and in the elimination of redundant
constraints (see Section 5). Otherwise, this is a
rare situation which might occur close to the solution, if the
termination criteria are too stringent.

- Termination occurred because the progress made
by the algorithm was no longer significant. See the description of
the input parameters
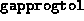 and
and  . This indicates
that the termination criteria may be too stringent. (If
. This indicates
that the termination criteria may be too stringent. (If 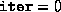 ,
then the initial point was probably already too close to the
boundary.)
,
then the initial point was probably already too close to the
boundary.)

- Termination occurred because either the primal or the
dual steplength became too small. If the infeasibility or
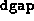 is
large, it is recommended to try restarting with either a reduced value
of
is
large, it is recommended to try restarting with either a reduced value
of  or with
or with 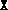 and
and 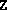 set to larger multiples of the
identity, or both. This is done automatically when the driver script
sdp.m is used, but is the user's responsibility when the
driver script is bypassed by a direct call to the function
fsdp.m. (If
set to larger multiples of the
identity, or both. This is done automatically when the driver script
sdp.m is used, but is the user's responsibility when the
driver script is bypassed by a direct call to the function
fsdp.m. (If 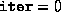 , then the initial guesses
, then the initial guesses 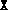 and
and
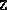 were most likely too close to the boundary of the positive
semidefinite cone. Adding a positive multiple of the identity to
were most likely too close to the boundary of the positive
semidefinite cone. Adding a positive multiple of the identity to 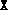 and/or
and/or 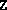 will rectify this.)
will rectify this.)

- Termination occurred because the maximum
number of iterations was reached. (If
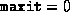 , then the data
passed the validation test.)
, then the data
passed the validation test.)

- Termination occurred because data failed
validation checks. This means that some input argument was not of the
correct dimension or fsdp.m was called with an incorrect
number of arguments. If
 , this could additionally mean
that the initial
, this could additionally mean
that the initial 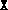 or
or 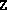 did not conform to the specified block
structure.
did not conform to the specified block
structure.
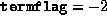
- Termination occurred because
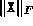 exceeded
exceeded 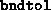 , indicating possible dual infeasibility.
, indicating possible dual infeasibility.
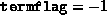
- Termination because
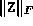 exceeds
exceeds
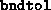 , indicating possible primal infeasibility.
, indicating possible primal infeasibility.
We encourage the reader to consult Appendix B which contains
a sample Matlab session illustrating the use of the sdp
script.




Next: Specialized Routines
Up: The script sdp.m
Previous: Invoking sdp.m or
Madhu Nayakkankuppam
Fri Mar 28 00:48:56 EST 1997
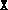 ,
, 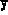 ,
, 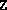
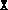 and
and 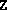 have multiple blocks, they are stored using
Matlab's sparse format. If they have only one block, then they are
always full.
have multiple blocks, they are stored using
Matlab's sparse format. If they have only one block, then they are
always full. 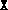 and
and 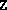 are numerically positive semidefinite in
the sense that Matlab's chol function does not encounter
negative pivots when applied to them.
are numerically positive semidefinite in
the sense that Matlab's chol function does not encounter
negative pivots when applied to them.
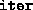
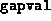
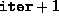 , with entries equal to the
value of
, with entries equal to the
value of 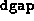 (
(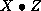 ) as a function of the iteration count.
The first entry in the
) as a function of the iteration count.
The first entry in the 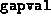 array is the value of
array is the value of 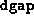 corresponding to the initial point provided.
corresponding to the initial point provided.

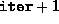 rows, whose
entries are the values of the primal and the dual objectives in the
first and the second columns respectively, as a function of the
iteration count.
rows, whose
entries are the values of the primal and the dual objectives in the
first and the second columns respectively, as a function of the
iteration count.
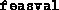
 rows, whose
entries are the values of
rows, whose
entries are the values of  and
and 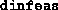 in the first and
the second columns respectively, as a function of the iteration count.
in the first and
the second columns respectively, as a function of the iteration count.
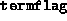


 is numerically
indefinite, i.e. chol(X) encountered a negative pivot. This
would not occur in exact arithmetic. The algorithm terminates,
returning the current iterate
is numerically
indefinite, i.e. chol(X) encountered a negative pivot. This
would not occur in exact arithmetic. The algorithm terminates,
returning the current iterate  (which is positive semidefinite).
This is normal, and usually means the problem is essentially solved
but the termination criteria were too stringent. (If
(which is positive semidefinite).
This is normal, and usually means the problem is essentially solved
but the termination criteria were too stringent. (If  ,
this means that the initial
,
this means that the initial 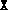 provided was not positive
semidefinite. This is easily remedied by adding a positive multiple
of the identity to
provided was not positive
semidefinite. This is easily remedied by adding a positive multiple
of the identity to 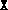 .)
.)

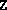 is numerically
indefinite, i.e. chol(Z) encountered a negative pivot. This
would not occur in exact arithmetic. The algorithm terminates,
returning the current iterate
is numerically
indefinite, i.e. chol(Z) encountered a negative pivot. This
would not occur in exact arithmetic. The algorithm terminates,
returning the current iterate 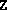 (which is positive semidefinite).
This termination flag is also used if chol finds that the new
iterate
(which is positive semidefinite).
This termination flag is also used if chol finds that the new
iterate 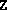 is numerically positive semidefinite, but the routine
blkeig finds that it has a zero (or negative) eigenvalue, in
which case the algorithm returns the new iterate, and then
terminates.
is numerically positive semidefinite, but the routine
blkeig finds that it has a zero (or negative) eigenvalue, in
which case the algorithm returns the new iterate, and then
terminates. Both cases are normal,
and they usually mean that the problem is essentially solved but that
the termination criteria were too stringent. (If
Both cases are normal,
and they usually mean that the problem is essentially solved but that
the termination criteria were too stringent. (If 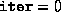 , this
means that the initial
, this
means that the initial 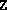 provided was not positive semidefinite.
This is easily remedied by adding a positive multiple of the identity
to
provided was not positive semidefinite.
This is easily remedied by adding a positive multiple of the identity
to 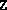 .)
.)

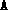 was
rank deficient. The routine preproc.m can help in detecting
inconsistent constraints and in the elimination of redundant
constraints (see Section 5). Otherwise, this is a
rare situation which might occur close to the solution, if the
termination criteria are too stringent.
was
rank deficient. The routine preproc.m can help in detecting
inconsistent constraints and in the elimination of redundant
constraints (see Section 5). Otherwise, this is a
rare situation which might occur close to the solution, if the
termination criteria are too stringent.

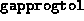 and
and  . This indicates
that the termination criteria may be too stringent. (If
. This indicates
that the termination criteria may be too stringent. (If 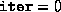 ,
then the initial point was probably already too close to the
boundary.)
,
then the initial point was probably already too close to the
boundary.)

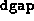 is
large, it is recommended to try restarting with either a reduced value
of
is
large, it is recommended to try restarting with either a reduced value
of  or with
or with 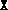 and
and 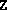 set to larger multiples of the
identity, or both. This is done automatically when the driver script
sdp.m is used, but is the user's responsibility when the
driver script is bypassed by a direct call to the function
fsdp.m. (If
set to larger multiples of the
identity, or both. This is done automatically when the driver script
sdp.m is used, but is the user's responsibility when the
driver script is bypassed by a direct call to the function
fsdp.m. (If 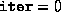 , then the initial guesses
, then the initial guesses 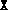 and
and
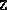 were most likely too close to the boundary of the positive
semidefinite cone. Adding a positive multiple of the identity to
were most likely too close to the boundary of the positive
semidefinite cone. Adding a positive multiple of the identity to 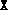 and/or
and/or 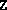 will rectify this.)
will rectify this.)

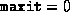 , then the data
passed the validation test.)
, then the data
passed the validation test.)

 , this could additionally mean
that the initial
, this could additionally mean
that the initial 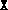 or
or 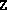 did not conform to the specified block
structure.
did not conform to the specified block
structure.
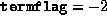
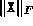 exceeded
exceeded 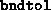 , indicating possible dual infeasibility.
, indicating possible dual infeasibility.
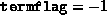
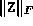 exceeds
exceeds
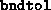 , indicating possible primal infeasibility.
, indicating possible primal infeasibility.