



Next: Support Routines
Up: Specialized Routines
Previous: Diagonally constrained problems
A specialized solver to compute the Lovász 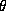 function of a
graph is also available. As in the diagonally constrained case, such
an SDP is solved much more efficiently by the XZ method than the
XZ+ZX method. The driver script is lsdp.m and the
specialized function is flsdp.m. The five steps involved in
setting up and solving a problem are again similar to Section 3,
except for the following important differences:
function of a
graph is also available. As in the diagonally constrained case, such
an SDP is solved much more efficiently by the XZ method than the
XZ+ZX method. The driver script is lsdp.m and the
specialized function is flsdp.m. The five steps involved in
setting up and solving a problem are again similar to Section 3,
except for the following important differences:
- The k--th constraint matrix
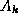 ,
, 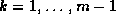 , is
, is
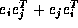 , where
, where 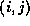 is the kth edge in the graph,
and
is the kth edge in the graph,
and 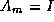 , with
, with 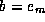 .
The user must provide a matrix G (an adjacency list with as many rows
as there are edges and 2 columns, each row of this matrix defining an edge) and
a weight vector w, with one component for each vertex of the graph.
The cost matrix C is defined by
.
The user must provide a matrix G (an adjacency list with as many rows
as there are edges and 2 columns, each row of this matrix defining an edge) and
a weight vector w, with one component for each vertex of the graph.
The cost matrix C is defined by
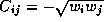 . (The optimal value of this SDP is actually
minus the value of the
. (The optimal value of this SDP is actually
minus the value of the 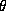 function of the graph.)
function of the graph.)
- The routine lsetpars.m sets parameters just as dsetpars.m
does.
- The initialization routine for the variables is called
linitvars.m, which expects the variables G
and w to be available in the Matlab workspace.
- Like dsdp.m, the script lsdp.m requires the parameter
useXZ to be available, and calls the specialized solver flsdp.m
only if useXZ equals 1 (the default value set by lsetpars.m).
Otherwise, it calls fsdp.m to solve the problem by
the XZ+ZX method, after constructing the matrices
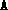 ,
, 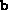 and
and 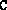 .
.
-
The problems that fall into this class are graph problems
that usually require the graph to be connected. Hence, these
specialized solvers have been purposefully designed to work with a
single block only. If validate is set to 1, flsdp.m
checks to see if the graph is connected and prints a warning if it is not.
- The user who wants a function interface can bypass the
script by typing:
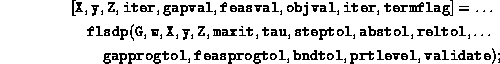
- When the output parameter
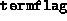 has the value 3, the
meaning is slightly different from the XZ+ZX case. Here,
has the value 3, the
meaning is slightly different from the XZ+ZX case. Here,  means that the Schur complement matrix, which is symmetric for the
XZ method, was numerically indefinite or singular, i.e. Matlab's
chol routine failed or generated a zero diagonal element.
means that the Schur complement matrix, which is symmetric for the
XZ method, was numerically indefinite or singular, i.e. Matlab's
chol routine failed or generated a zero diagonal element.
Appendix B contains sample Matlab sessions that illustrate
the use of dsdp.m and lsdp.m on these special types
of problems.




Next: Support Routines
Up: Specialized Routines
Previous: Diagonally constrained problems
Madhu Nayakkankuppam
Fri Mar 28 00:48:56 EST 1997
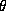 function of a
graph is also available. As in the diagonally constrained case, such
an SDP is solved much more efficiently by the XZ method than the
XZ+ZX method. The driver script is lsdp.m and the
specialized function is flsdp.m. The five steps involved in
setting up and solving a problem are again similar to Section 3,
except for the following important differences:
function of a
graph is also available. As in the diagonally constrained case, such
an SDP is solved much more efficiently by the XZ method than the
XZ+ZX method. The driver script is lsdp.m and the
specialized function is flsdp.m. The five steps involved in
setting up and solving a problem are again similar to Section 3,
except for the following important differences:
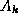 ,
, 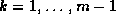 , is
, is
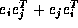 , where
, where 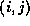 is the kth edge in the graph,
and
is the kth edge in the graph,
and 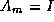 , with
, with 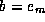 .
The user must provide a matrix G (an adjacency list with as many rows
as there are edges and 2 columns, each row of this matrix defining an edge) and
a weight vector w, with one component for each vertex of the graph.
The cost matrix C is defined by
.
The user must provide a matrix G (an adjacency list with as many rows
as there are edges and 2 columns, each row of this matrix defining an edge) and
a weight vector w, with one component for each vertex of the graph.
The cost matrix C is defined by
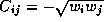 . (The optimal value of this SDP is actually
minus the value of the
. (The optimal value of this SDP is actually
minus the value of the 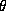 function of the graph.)
function of the graph.)
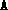 ,
, 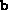 and
and 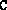 .
.
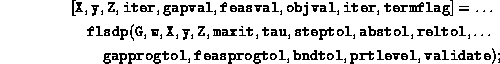
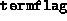 has the value 3, the
meaning is slightly different from the XZ+ZX case. Here,
has the value 3, the
meaning is slightly different from the XZ+ZX case. Here,  means that the Schur complement matrix, which is symmetric for the
XZ method, was numerically indefinite or singular, i.e. Matlab's
chol routine failed or generated a zero diagonal element.
means that the Schur complement matrix, which is symmetric for the
XZ method, was numerically indefinite or singular, i.e. Matlab's
chol routine failed or generated a zero diagonal element.