Fast Algorithms at Courant
Research
Large-scale linear systems arise in a myriad of areas in physics, mathematics, and statistics. Often when directly discretizing PDEs, the resulting linear systems are sparse and efficient methods for applying the discretized operators are straightforward, and relatively efficient methods for computing their inverse has been developed. However, linear systems arising from the discretization of integral formulations of the very same PDEs are dense, and somewhat more sophisticated algorithms must be developed in order to apply and invert there operators with near optimal computational complexity. Often these algorithms are based on the underlying physics of the problem, and are therefore commonly referred to as analysis-based fast algorithms.
The most well-known analysis-based fast algorithm algorithm is the fast multipole method, which allows for various N-body calculations to be performed in O(N) time, often resulting in speedups over the direct calculation of 1000x or more. Most of the work of the Fast Algorithms group is focused on designing novel computational schemes for solving PDE and integral equations arising in electromagnetics, fluid dynamics, quantum electrodynamics, heat flow, and magnetohydrodynamics. Various aspects of the work include numerical quadrature design, special function evaluation, applied analysis (e.g. deriving novel integral equations), computational geometry (e.g. surface meshing), optimization, and high-performance computing.
People
Students
Tristan GoodwillYuwei Jiang
Sunli Tang
Evan Toler
Seminar
The group will meet during Fall 2019 on Thursdays from
2:00pm - 3:30 in CIWW 705.
Working group for Spring 2019.
Code
Boundary integral equation solvers
FMM-accelerated boundary integral equation solvers in
complex geometries in three dimensions for Laplace and
Helmholtz problems (and soon Maxwell).
GitLab
Fast multipole methods
FMMs in three dimensions for Laplace and Helmholtz
potentials. Maintained by the Flatiron Institute.
GitHub
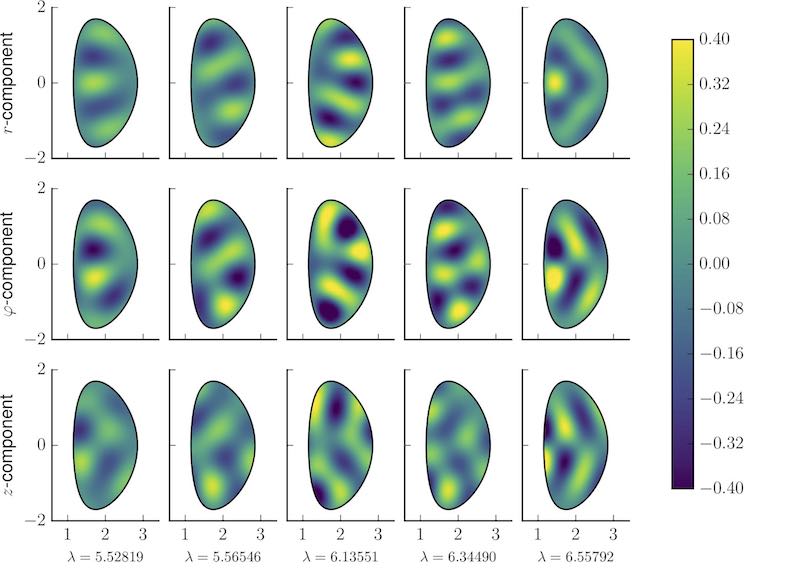
Taylor states in stellarators
High-order boundary integral equation code for computing
MHD equilibria in stellarator geometries, see paper
Taylor States in Stellerators above.
GitHub
Quadrature for magnetostatics
High-order quadrature for layer potentials on smooth
toroidal surfaces, see paper
Efficient high-order singular quadrature
schemes in magnetic fusion above.
Plasma physics
Various simulators for plasma equilibria in axisymmetric
geometries (e.g. tokamaks) have been developed by members
of the group. Links to individual codes can be found
here.
Funding
The group is supported in part by the following sources:
Hidden Symmetries and Fusion Energy
A. Bhattacharjee (PI), Cerfon (Co-I), O'Neil (Co-I),
et. al., Simons Foundation, 6/1/18 - 5/31/22
Multi-level randomized algorithms for
high-frequency wave propagation
Greengard (PI) and O'Neil (Co-I), Office of Naval Research Award
#N00014-18-1-2307, 6/1/18 - 5/31/22
Toward real-time electromagnetic design: Fast,
accurate, and robust integral equation-based solvers
O'Neil (PI), Office of Naval Research Award
#N00014-17-1-2451, 6/1/17 - 5/31/20
Fast high-order CAD-compatible Nystrom methods for
frequency domain electromagnetics
O'Neil (PI), Office of Naval Research Award
#N00014-17-1-2059, 1/1/17 - 12/31/19
Plasma Properties (Task III)
H. Weitzner (PI) and Cerfon (Co-I), US Department of Energy,
Office of Science, Fusion Energy Sciences DE-FG02-86ER53223,
5/1/16 - 4/30/19
High Performance Equilibrium Solvers for
Integrated Magnetic Fusion Simulations
Cerfon
(PI), US Department of Energy, Office of Science, Fusion
Energy Sciences DE-SC0012398, 7/15/14 - 7/14/19



Publications and Technical Reports
| Title, author, journal | Download |
|---|---|
| Efficient high-order singular quadrature
schemes in magnetic fusion D. Malhotra, A. J. Cerfon, M. O'Neil, and E. Toler, submitted, 2019. |
arXiv |
| Magnetic shear due to localized toroidal flow
shear in tokamaks J. Lee and A. J. Cerfon, Plasma Physics and Controlled Fusion, 61:105007, 2019. |
journal |
| Taylor States in Stellarators: A Fast
High-order Boundary Integral Solver D. Malhotra, A. J. Cerfon, L.-M. Imbert-Gerard, and M. O'Neil, J. Comput. Phys., 397:108791, 2019. |
journal |
| An FFT-accelerated direct solver for
electromagnetic scattering from penetrable
axisymmetric objects
J. Lai and M. O'Neil, J. Comput. Phys., 390:152-174, 2019. |
journal arXiv:1810.07067 |
| A high-order wideband direct
solver for electromagnetic scattering
from bodies of revolution
C. L. Epstein, L. Greengard, and M. O'Neil, J. Comput. Phys., 387:205-229, 2019. |
journal arXiv:1708.00056 |
| A flux-balanced fluid model for
collisional plasma edge turbulence: Model
derivation and basic physical features A. J. Majda, D. Qi, and A. J. Cerfon, Phys. Plasmas, 25:102307, 2018. |
journal |
| A flux-balanced fluid model for collisional plasma edge turbulence: Numerical simulations with different aspect ratios A. J. Majda, D. Qi, and A. J. Cerfon, Phys. Plasmas, 26:082303, 2019. |
journal |
| Second-kind integral equations for the
Laplace-Beltrami problem on surfaces
in three dimensions M. O'Neil, Adv. Comput. Math., 44(5): 1385-1409, 2018. |
journal (open-access) |
| An integral equation-based numerical
solver for Taylor states in toroidal
geometries M. O'Neil and A. J. Cerfon, J. Comput. Phys., 359:263-282, 2018. |
journal arXiv:1611.01420 |
| Pseudo spectral collocation with Maxwell
polynomials for kinetic equations with energy
diffusion T. Sanchez-Vizuet and A. J. Cerfon, Plasma Physics and Controlled Fusion, 60:025018, 2018. |
journal |
| An adaptive fast multipole accelerated
Poisson solver for complex geometries T. Askham and A. J. Cerfon, J. Comput. Phys., 344:1, 2017. |
journal |
| Sparse grid techniques for
particle-in-cell schemes L. F. Ricketson and A. J. Cerfon, Plasma Physics and Controlled Fusion, 59:024002, 2017. |
journal |
| Fast algorithms for Quadrature by
Expansion I: Globally valid expansions M. Rachh, A. Klöckner, and M. O'Neil, J. Comput. Phys., 345:706-731, 2017. |
journal arXiv:1602.05301 |
| Accurate Derivative Evaluation for any
Grad-Shafranov Solver L. F. Ricketson, A. J. Cerfon, M. Racch, and J. P. Freidberg, J. Comput. Phys., 305:744, 2016. |
journal |
| ECOM: A fast and accurate solver for
toroidal axisymmetric MHD equilibria J. P. Lee and A. J. Cerfon, Comput. Phys. Commun., 190:72, 2015. |
journal |