Research topics
My expertise is in the areas of applied and computational mathematics, computational materials science, and computational physics. More generally, I am interested in the development of widely-applicable mathematical and algorithmic methodologies for the modeling of complex natural systems at the atomistic and mesoscopic levels, and their application to practical problems in fundamental and applied sciences and engineering. In particular, I work on developing algorithms that accelerate or systematically coarse-grain traditional methods such as Molecular Dynamics or (Kinetic) Monte Carlo, as well as multi-scale (hybrid) methods combining particle with stochastic (fluctuating) coarse-grained models. My present focus is on fluid dynamics at small scales, and in particular, fluctuating hydrodynamics. Visit the Computer Codes page for public-domain codes incorporating our work.
I am the lead PI on an NSF RTG on Modeling and Simulation (DMS-1646339), and co-lead IRG-1 of the NYU MRSEC center (DMR-1420073). My research at the Courant Institute is and has been funded by National Science Foundation grants NSF DMS-2052515, DMS-1115341, DMS-1418706, CBET-1706562 and CBET-1804940, the Air Force's Young Investigator Research Program (2012-2015), and the Department of Energy (DOE) Office of Science Early Career Research Program (2012-2017).
Specific details on several research subjects I have or am working on (with latest work first) can be found below. There are many interesting projects for undergraduate and graduate students in each of these areas, ranging from developing novel algorithms to applying computational methods to relevant problems in the sciences and engineering.
Hydrodynamics at Small Scales
This research focuses on fluid mechanics in regimes where thermal fluctuations are important. Notable examples include flows at micro and nano scales typical of new microfluidic, nanofluidic and microelectromechanical devices; complex fluids such as colloidal suspensions common in chemical engineering, biological systems such as lipid membranes, Brownian molecular motors, nanopores; as well as processes where the effect of fluctuations is amplified by strong non-equilibrium effects, such as combustion of lean flames, capillary dynamics, hydrodynamic instabilities, and others.
There are several main avenues of research, described next.
Dynamics for Suspensions of Semi-Flexible Fibers/Polymers
The cell cytoskeleton is composed of stiff slender fibers such as actin filaments and microtubules. Together with Ph.D. student Ondrej Maxian and colleague Alex Mogilner we have been developing numerical methods to model cross-linked actin gels and using the codes to study question in math biology and biophysics related to the structure and rheology of such gels. This work is funded in part through an NSF grant DMS-2052515 on "Computational modeling of cytoskeleton-cytoplasm mechanics at the mesoscale." Codes and examples are available in our SlenderBody repo.This work is described in the following papers (but I strongly recommend reading the Ph.D. thesis by Dr. Ondrej Maxian on "Hydrodynamics of transiently cross-linked actin networks: theory, numerics, and emergent behaviors" instead):
1. "An integral-based spectral method for inextensible slender fibers in Stokes flow" by O. Maxian, A. Mogilner and A. Donev, Phys. Rev. Fluids, 6:014102, 2021 [ArXiv:2007.11728], see also movies, and followup paper "The hydrodynamics of a twisting, bending, inextensible fiber in Stokes flow", by O. Maxian, B. Sprinkle, C. S. Peskin, and A. Donev, Phys. Rev. Fluids, 2022 [ArXiv:2201.04187].
2. "Simulations of dynamically cross-linked actin networks: morphology, rheology, and hydrodynamic interactions" by O. Maxian, R. P. Peláez, A. Mogilner, and A. Donev, submitted to PLOS Comp. Bio., 2021 [bioRxiv.org:2021.07.07.451453], see also supplementary movies.
3. "Interplay between Brownian motion and cross-linking kinetics controls bundling dynamics in actin networks" by O. Maxian, A. Donev, and A. Mogilner, submitted to Biophysical J., 2021 [bioRxiv:021.09.17.460819], see also supplementary movies.
4. "The hydrodynamics of a twisting, bending, inextensible fiber in Stokes flow", by O. Maxian, B. Sprinkle, C. S. Peskin, and A. Donev, Phys. Rev. Fluids, 7, 074101, 2022 [ArXiv:2201.04187], see also supplementary movies.
5. "Bending fluctuations in semiflexible, inextensible, slender filaments in Stokes flow: towards a spectral discretization" by O. Maxian, B. Sprinkle, and A. Donev, to appear in J. Chem. Phys., 2023, [ArXiv:2301.11123], see also supplementary movies.
Here is a movie (MP4) showing a dynamically cross-linked homogeneous network under cyclic shear, without Brownian motion (left), or with fluctuations (right):

Brownian Dynamics for Colloidal Suspensions
The study of complex fluids such as micro- and nano-colloidal or polymeric solutions is an important application of fluctuating hydrodynamics. We have previously used a particle method to study the dynamics of polymer chains in solution. We are presently developing methods to directly couple immersed particles to a fluctuating fluid medium. This has led to new algorithms for Brownian Dynamics of colloidal suspensions that are an order of magnitude faster than existing methods, and can handle hundreds of thousands of particles because they can be made to scale linearly with the number of colloidal particles. This work is in collaboration with a number of colleagues, including the research group of Neelesh Patankar at Northwestern and Boyce Griffith at UNC.We have recently applied some of our methods to study the dynamics of active suspensions of colloidal microrollers, micron-sized spheres rotated by an external magnetic field above a bottom wall, as studied in recent experiments in the group of collaborator Paul Chaikin at NYU Physics, as discussed in more details in these papers (see our RigidMultiblobsWall github for codes):
1. "Unstable fronts and motile structures formed by microrollers", M. Driscoll, B. Delmotte, M. Youssef, S. Sacanna, A. Donev and P. Chaikin, Nature Physics, 13, 375–379, 2017, [ArXiv:1609.08673]. See also the News & Views associated with the paper. These simulations predicted the existence of critters, seen in this movie.
Here is a movie of the formation of "critters" predicted by our simulations:

2. "Sedimentation of a colloidal monolayer down an inclined plane" by B. Sprinkle, S. Wilken, S. Karapetyan, M. Tanaka, Z. Chen, J. R. Cruise, B. Delmotte, M. M. Driscoll, P. Chaikin and A. Donev, Phys. Rev. Fluids, 6:034202, 2021 [ArXiv:2011.14472]. Here is a movie of a simulation (Fig. 1 in paper).
3. "Driven dynamics in dense suspensions of microrollers" by B. Sprinkle, E. B. van der Wee and Y. Luo and M. Driscoll, and A. Donev, Soft Matter, 16, 7982 - 8001, 2020 [ArXiv:2005.06002]. Here is a movie illustrating the two-layer structure of driven uniform suspension of microrollers (Fig. 2 in the paper).
4. "Large Scale Brownian Dynamics of Confined Suspensions of Rigid Particles", B. Sprinkle, F. Balboa Usabiaga, N. A. Patankar and A. Donev, submitted to J. Chem. Phys., 2017 [ArXiv:1709.02410].
5. "Brownian Dynamics of Confined Suspensions of Active Microrollers", F. Balboa Usabiaga, B. Delmotte and A. Donev, J. Chem. Phys., 146, 134104, 2017 [ArXiv:1612.00474]. See our RigidMultiblobsWall github for codes, and the Supplementary Material Movies.
Here is a movie illustrating the two-layer structure of driven uniform suspension of microrollers simulated using lubrication-corrected Brownian Dynamics, and here is an animation of a uniform suspension of microrollers simulated using the rigid multiblob method (see paper #4 above):

A key idea used in our work is to employ fluctuating hydrodynamics as a tool to accelerate traditional Brownian dynamics simulations, and also as a way to enable coupling of particles to complex liquid mixtures (e.g., chemical fluid mixtures in active suspensions). This work is described in the following papers:
1. "Inertial Coupling Method for particles in an incompressible fluctuating fluid", F. Balboa Usabiaga and R. Delgado-Buscalioni and B. E. Griffith and A. Donev, Computer Methods in Applied Mechanics and Engineering, 269:139-172, 2014 [ArXiv:1212.6427].
2. "Brownian Dynamics without Green's Functions", S. Delong, F. Balboa Usabiaga, R. Delgado-Buscalioni, B. E. Griffith and A. Donev, 2014, J. Chem. Phys., 140, 134110, 2014 [ArXiv:1401.4198].
3. "Rapid Sampling of Stochastic Displacements in Brownian Dynamics Simulations", by A. M. Fiore, F. Balboa Usabiaga, A. Donev and J. W. Swan, J. Chem. Phys., 146, 124116, 2017 [Arxiv:1611.09322]. See our PSE github for codes.
4. "A fluctuating boundary integral method for Brownian suspensions", Y. Bao, M. Rachh, E. Keaveny, L. Greengard and A. Donev, submitted to J. Comp. Phys., 2017 [ArXiv:1709.
5. "Brownian Dynamics of Fully Confined Suspensions of Rigid Particles Without Green's Functions", by B. Sprinkle, A. Donev, A. Pal Singh Bhalla and N. Patankar, J. Chem. Phys., 150, 164116, 2019 [ArXiv:1901.06427]. Here is a movie for Fig. 5 in section V.B showing defect propagation in a confined colloidal monolayer.
Numerical schemes for fluctuating hydrodynamics
Thermal fluctuations can be included in the classical Navier-Stokes fluid equations through stochastic forcing terms that are essentially the divergence of a white-noise random field (stochastic flux), as first proposed by Landau and Lifshitz. The presence of non-trivial dynamics at all scales, as well as the necessity to maintain fluctuation-dissipation balance in spatio-temporal discretizations, makes the continuum stochastic partial differential equations of fluctuating hydrodynamics difficult to solve using existing approaches.Here is, for example, an animation produced by collaborator Andy Nonaka showing the development of an instability during diffusive mixing of a solution of salt on top of a solution of sugar (see paper #3 below), in good agreement with experimental observations reported in the bottom row of panels in Fig. 1 of the paper "Mixed-mode instability of a miscible interface due to coupling between Rayleigh-Taylor and double-diffusive convective modes" by the group of Anne De Wit. In this simulation the instability is triggered entirely by thermal fluctuations, that is, starting with no initial interface perturbation.
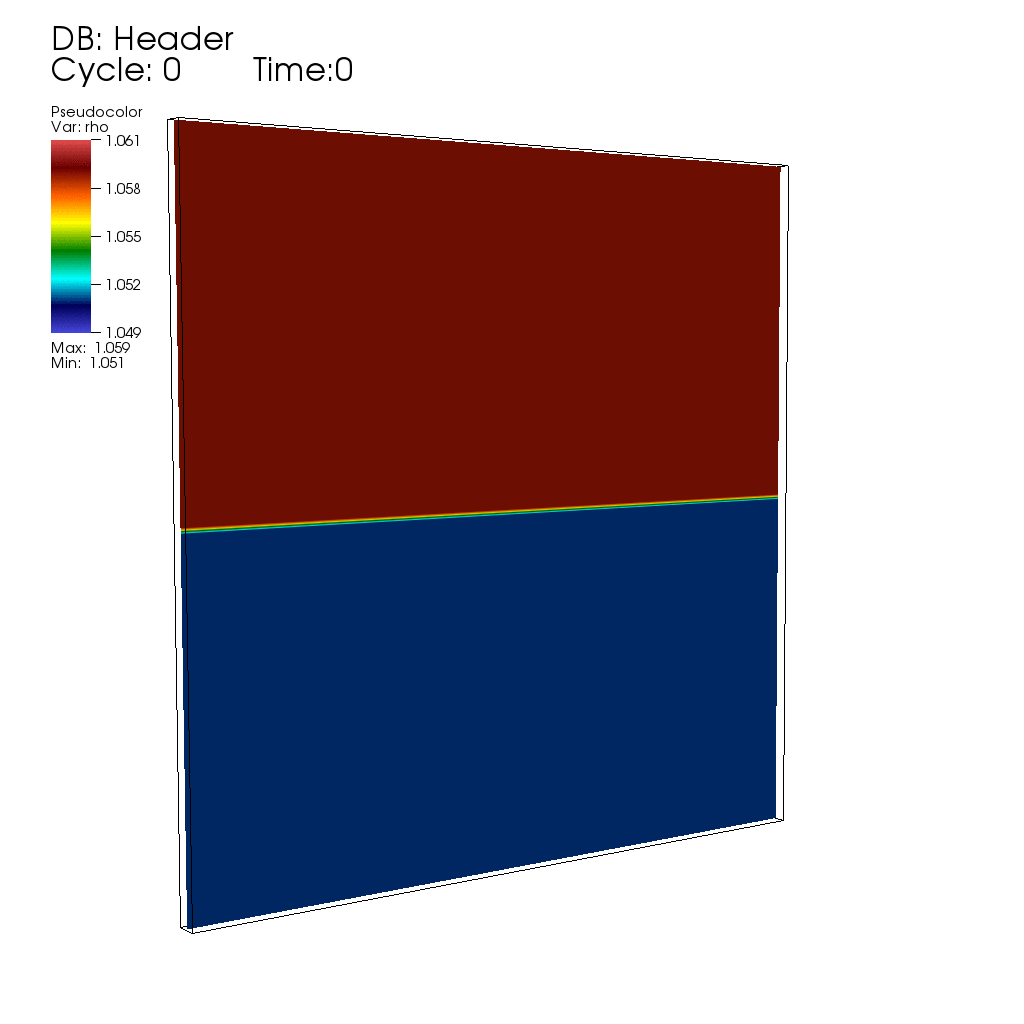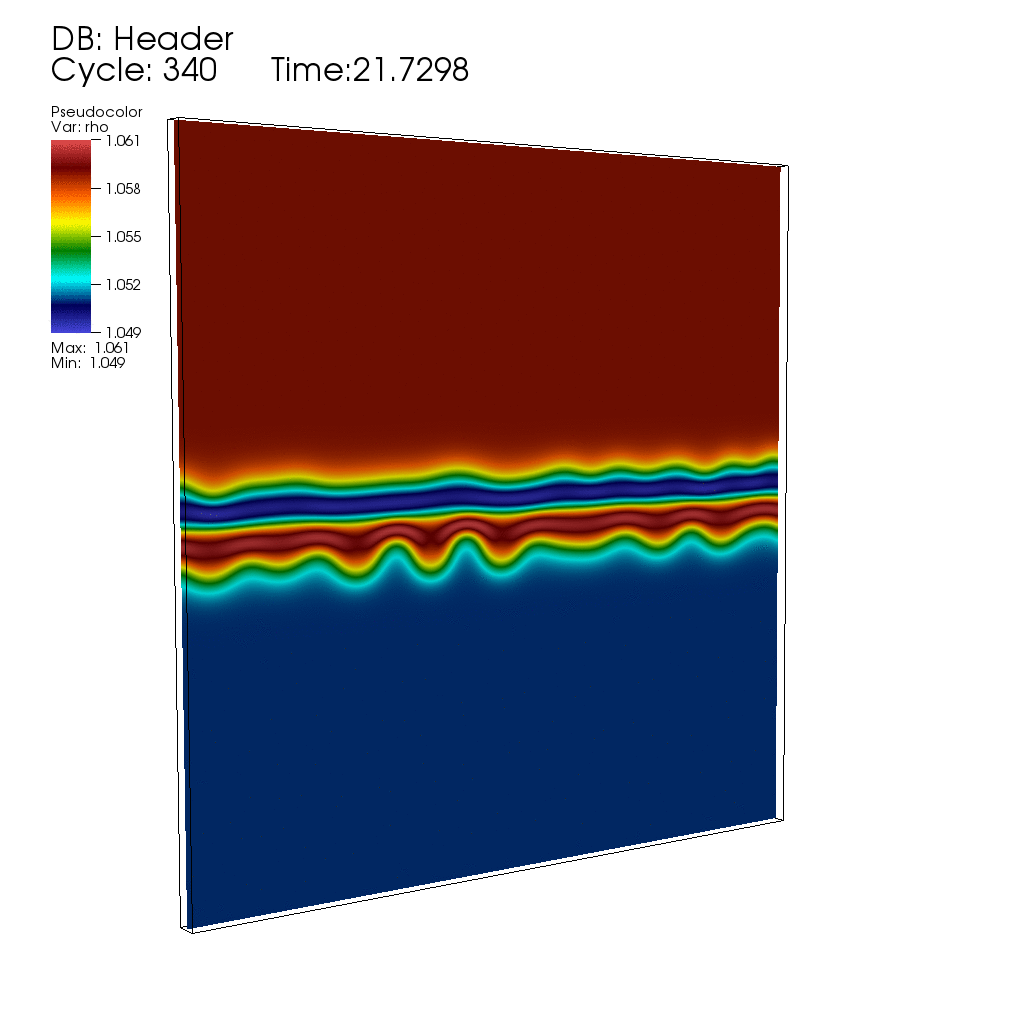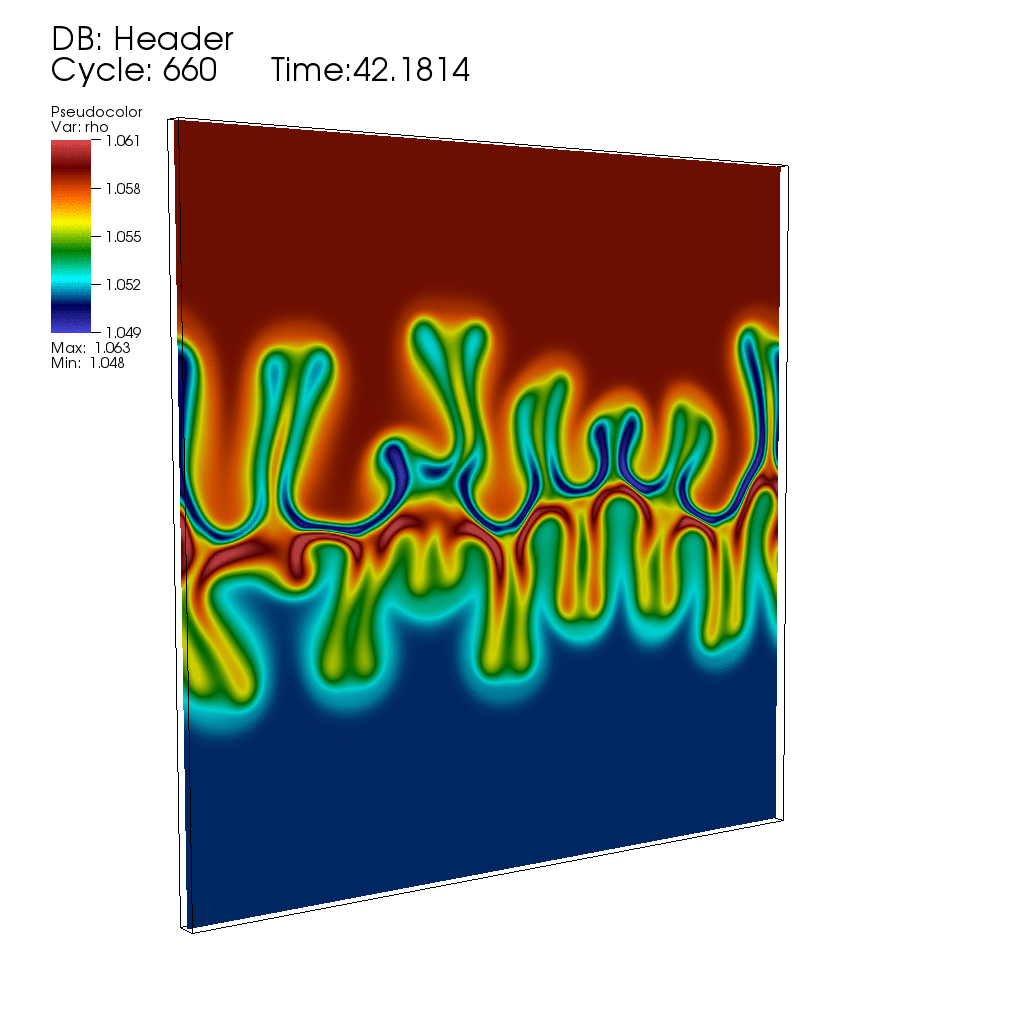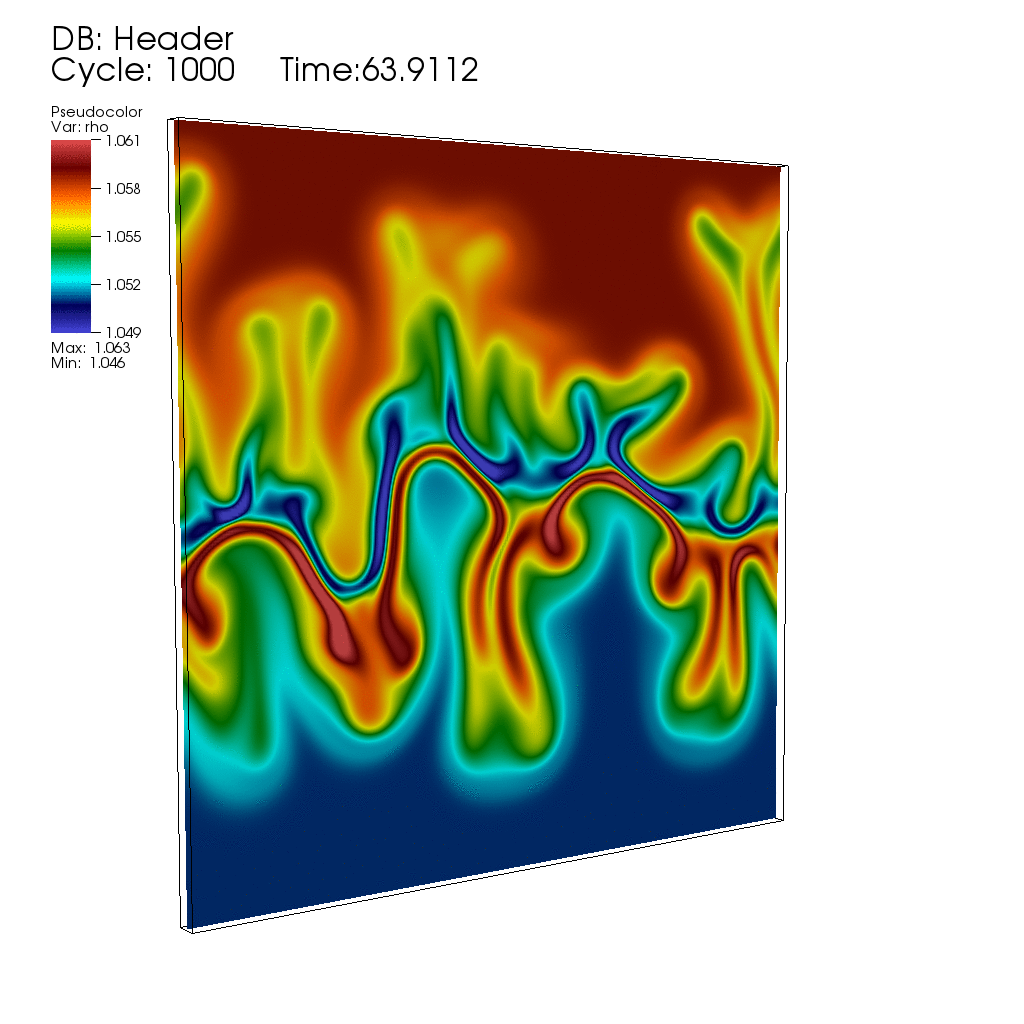
My work in this field is joint with several collaborators, whose webpages contain additional information and publications of interest. In particular, I collaborate closely with John Bell (Lawrence Berkeley National Laboratory) and Alejandro Garcia (San Jose State University), Rafael Delgado-Buscalioni (UAM, Spain), Eric Vanden-Eijnden (Courant), and Boyce Griffith (UNC). Our work builds on the mature field of deterministic computational fluid dynamics, and combines fundamental cross-disciplinary investigations with development of extensible yet efficient parallel computer codes (in particular, our algorithms are incorporated into the BoxLib and IBAMR codes, and presently also extended to run on GPUs).
Here is an animation produced by collaborator Changho Kim showing the propagation of a spherical chemical wave leaving behind a Turing-like pattern, without thermal fluctuations (left) and with fluctuations (right):
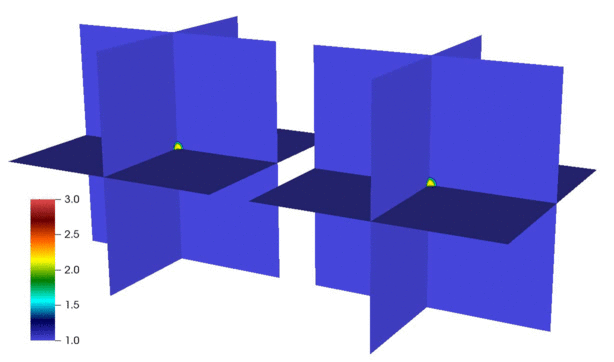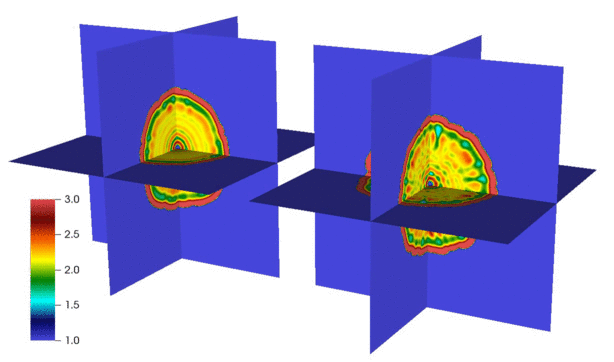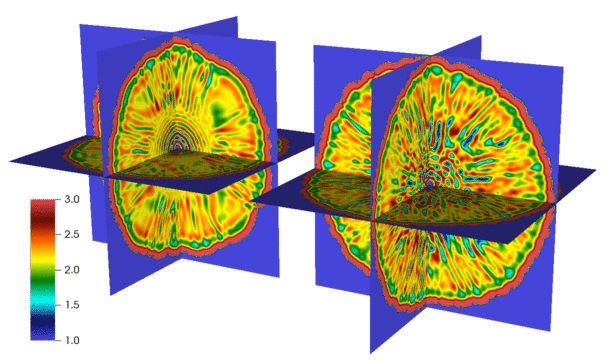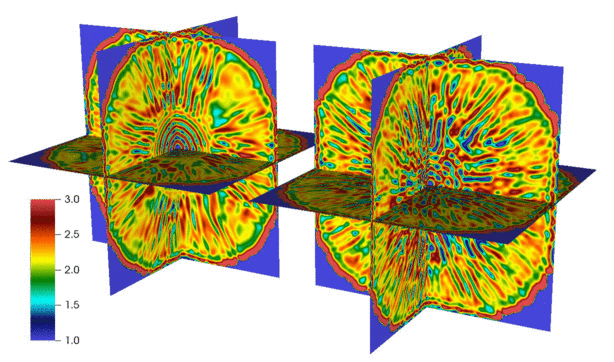
We have developed numerical methods for fluctuating hydrodynamics of complex fluid mixtures, including mixtures of many gases and liquids, chemically-reactive mixtures, multiphase mixtures, and electrolyte mixtures. Here are some selected papers on this topic:
1. "Modeling Multi-phase Flow using Fluctuating Hydrodynamics", A. Chaudhri, J. B. Bell, A. L. Garcia and A. Donev, submitted to Phys. Rev. E, 2014, [ArXiv:1407.6749].
2. "Fluctuating hydrodynamics of multispecies reactive mixtures", A. K. Bhattacharjee, K. Balakrishnan, A. L. Garcia, J. B. Bell and A. Donev, J. Chem. Phys., 142, 224107, 2015 [ArXiv:1503.07478].
3. "Low Mach Number Fluctuating Hydrodynamics of Multispecies Liquid Mixtures", A. Donev and A. J. Nonaka and A. K. Bhattacharjee and A. L. Garcia and J. B. Bell, Physics of Fluids, 27(3):037103, 2015 [ArXiv:1412.6503].
4. "Low Mach Number Fluctuating Hydrodynamics for Electrolytes", J.-P. Peraud, A. Nonaka, A. Chaudhri, J. B. Bell, A. Donev and A. L. Garcia, Phys. Rev. F, 1(7):074103, 2016 [ArXiv:1607.05361].
In addition to developing state-of-the-art numerical methods and studying the fundamental physics of thermal fluctuations in fluids, as for example in the papers
5. "Reversible Diffusion by Thermal Fluctuations", A. Donev, T. G. Fai, and E. Vanden-Eijnden, chapter 5 in the Proceedings from the Symposium in Honor of Dr Berni Alder's 90th birthday, 2017 [ArXiv:1306.3158].
6. "Fluctuation-enhanced electric conductivity in electrolyte solutions", J.-P. Peraud, A. Nonaka, A. Chaudhri, J. B. Bell, A. Donev and A. L. Garcia, to appear in PNAS, 2017 [ArXiv:1706.06227].
we have performed a number of comparisons with experiments, as described, for example, in the paper:
7. "Dynamic scaling for the growth of non-equilibrium fluctuations during thermophoretic diffusion in microgravity", R. Cerbino, Y. Sun, A. Donev and A. Vailati, Scientific Reports, 5:14486, 2015 [ArXiv:1502.03693].
Present work is focused on:
1. Accounting for chemical reactions in complex liquid mixtures in a low Mach setting in a way consistent with nonequilibrium thermodynamics.
2. Further work on electrolyte solutions including implicit electroneutral methods, weak electrolytes, and surface reactions including electrochemical flows.
3. Non-equilibrium "giant" fluctuations in diffusive processes in quasi-two-dimensional geometries, such as diffusion near interfaces, boundaries, and on membranes.
Particle methods for hydrodynamics
Thermal fluctuations can be included in fluid dynamics by explicitly accounting for the particle nature of matter using particle methods. It is also important to perform efficient particle calculations in order to assess and expand the range of validity of continuum approximations. Our research focuses on developing coarse-grained stochastic particle models that build upon the Direct Simulation Monte Carlo (DSMC) method. This class of methods are also related to the dissipative particle dynamics (DPD) and the multi-particle collision (also called stochastic rotation) dynamics techniques. Further details can be found in this presentation or the following papers:1. "A Thermodynamically-Consistent Non-Ideal Stochastic Hard Sphere Fluid", by A. Donev and A. L. Garcia and B. J. Alder, J. Stat. Mech., P11008, 2009 [arXiv:0908.0510].
2. "Stochastic Hard-Sphere Dynamics for Hydrodynamics of Non-Ideal Fluids", by A. Donev, A. L. Garcia and B. J. Alder, Phys. Rev. Lett., 101:075902, 2008 [arXiv:0803.0359].
3. "Stochastic Event-Driven Molecular Dynamics", by A. Donev, A. L. Garcia and B. J. Alder, J. Comp. Phys., 227(4):2644-2665, 2008, [arXiv:0708.0251].
Our present research is focused on extending these types of algorithms to multi-species reactive mixtures, implementing the algorithms in a public domain code that we will release in the future, as well as parallelizing the particle algorithms.
Hybrid particle-continuum algorithms
Particle and continuum methods can be combined into hybrid multiscale methods that use the more expensive but accurate particle method only in regions where the continuum description fails or is difficult to implement (e.g., shocks, rarefication, singularities, near suspended structures). This can substantially lower the cost of particle methods while still keeping the advantages of particle methods in regions of interest.This image illustrates how three different aspects of my research are combined to study the dynamics of a polymer chain in shear flow. The chain itself is made up of hard disks (red, done using event-driven molecular dynamics) and suspended in a coarse-grained particle solvent (green, done using our I-DSMC algorithm), further embedded in a stochastic continuum fluid flow (purple arrows show the fluctuating velocities in our RK3D fluctuating hydrodynamics solver):
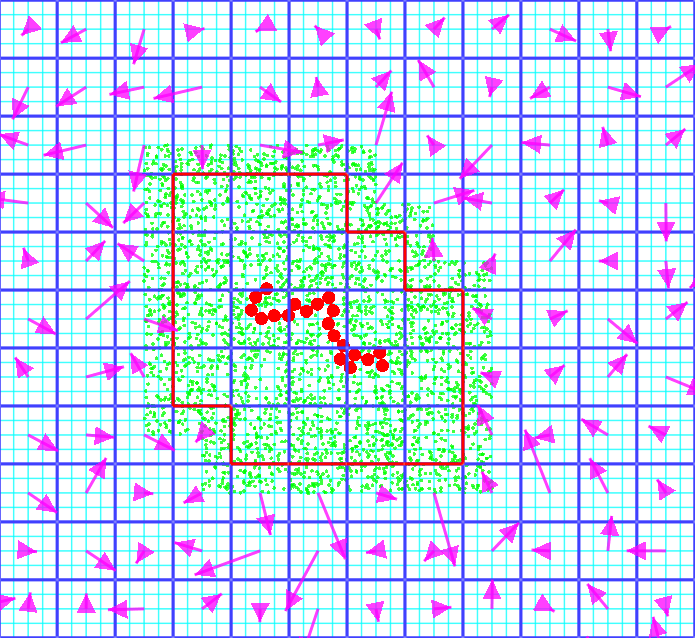
We have developed a bidirectional dynamic coupling between a stochastic particle fluid and a fluctuating continuum and demonstrated that thermal fluctuations have to be consistently included in the continuum component of hybrid calculations in order not to distort the thermal equilibrium in the particle solver. Here is a presentation (without the movies) on the subject, with details contained in this paper:
1. "A hybrid particle-continuum method for hydrodynamics of complex fluids", by A. Donev and J. B. Bell and A. L. Garcia and B. J. Alder, SIAM J. Multiscale Modeling and Simulation 8(3):871-911, 2010 [arXiv:0910.3968].
There are severe time step restrictions inherent to both particle and hybrid calculations, stemming from the need to resolve the dynamics of the fluid particles. In order to extend the time step, one needs to avoid the particle representation in the solver, as we do in more recent work described above.
Event-Driven Asynchronous Algorithms
Rather broadly, I am interested in the development of efficient particle methods, specifically asynchronous event-driven Molecular Dynamics and Kinetic Monte Carlo methods. My research in particle packings, reaction-diffusion systems, and coarse-grained solvents, all use an event-driven framework to achieve substantial speedup over traditional time-driven methods, as described in this presentation and this review article:
1. "Asynchronous Event-Driven Particle Algorithms", by A. Donev, SIMULATION: Transactions of the Society for Modeling and Simulation International, 85(4):229-242, 2009.
An important remaining challenge for future research is efficient parallelization of asynchronous event-driven algorithms.
Diffusion-Reaction Systems
Together with collaborators at Lawrence Livermore National Labs we developed an event-driven Kinetic Monte Carlo algorithm for diffusion-reaction systems that is far superior to traditional algorithms. This method has the potential to be applied in a variety of problems in material science and biology. Notably, we have used it to study radiation damage in metals, and the method has been implemented for biochemical reactive systems in the eGFRD code. Further details can be found in this presentation and these papers:1. "First-passage Kinetic Monte Carlo method", by T. Oppelstrup, V. V. Bulatov, A. Donev, M. H. Kalos, G. H. Gilmer and B. Sadigh, Phys. Rev. E, 80(6):066701, 2009 [arXiv:0905.3575].
2. "A First-Passage Kinetic Monte Carlo Algorithm for Complex Diffusion-Reaction Systems", by A. Donev, V. V. Bulatov, T. Oppelstrup, G. H. Gilmer, B. Sadigh and M. H. Kalos, J. Comp. Phys., 229(9):3214-3236, 2010 [arXiv:0905.3576].
Future work will extend these methods to enable a mixed time-driven with event-driven framework that combines the advantages of each approach, without the inefficiency of time-driven algorithms or the complexity of purely event-driven handling.
Packing of Hard Particles
My Ph.D. dissertation (thesis) and my Final Oral Exam (FPO) presentation (June 9th, 2006) give a rather extensive overview of my research on Jammed Packings of Hard Particles, performed under the supervision of Dr. Salvatore Torquato as part of the Complex Materials Theory Group. Here are some MNG and GIF animations related to my thesis research.
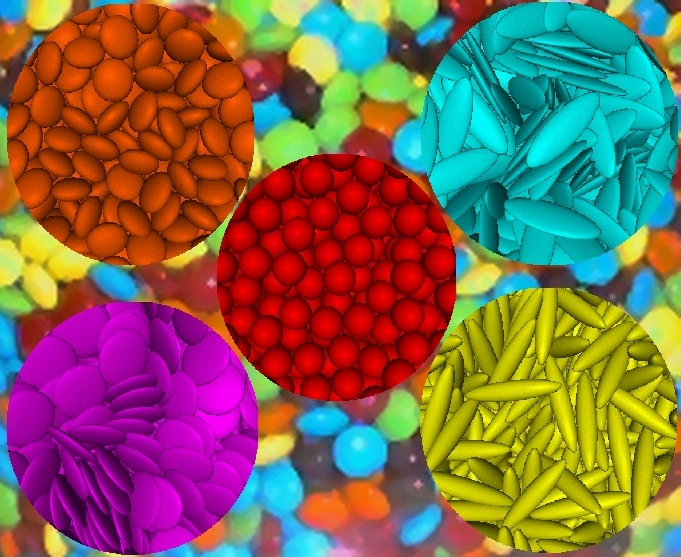
You can find executable versions of my molecular dynamics packing codes along with some instructions here. These codes were used to make the packings of hard ellipsoids shown to the left on top of an experimental packing of M&M prolate ellipsoids.
I have also developed dynamic VRML models to render and animate packings of spheres and ellipsoids. These are barely documented but you can get them here if you are brave.
Rigidity Theory and Jamming
By using mathematical results from rigidity theory, in collaboration with Robert Connelly, we were able to develop a rigorous framework for defining and testing for jammed packings of hard spheres and ellipsoids, as described in these papers:1. "Underconstrained Jammed Packings of Hard Ellipsoids", by A. Donev, R. Connelly, F. H. Stillinger and S. Torquato, Phys. Rev. E, 75:051304, 2007 [cond-mat/0608334].
2. "A Linear Programming Algorithm to Test for Jamming in Hard-Sphere Packings", by A. Donev, S. Torquato, F. H. Stillinger, and R. Connelly, J. Comp. Phys., 197(1):139-166, 2004.
3. "Comment on "Jamming at zero temperature and zero applied stress: The epitome of disorder", by A. Donev, S. Torquato, F. H. Stillinger, and R. Connelly, Phys. Rev. E, 70:043301, 2004.
4. "Jamming in Hard Sphere and Disk Packings", by A. Donev, S. Torquato, F. H. Stillinger, and R. Connelly, J. Appl. Phys., 95(3):989, 2004.
5. "Breakdown of Elasticity Theory for Jammed Hard-Particle Packings: Conical Nonlinear Constitutive Theory", by S.Torquato, A. Donev, and F. H. Stillinger, Int. J. Solids Structures, 40(25):7143-7153, 2003.
Further work is necessary to develop codes that can analyze the rigidity properties of large-scale packings.
Packing of Hard Ellipsoids
We further developed sophisticated event-driven molecular dynamics algorithms and codes to generate jammed packings of hard spheres and also, for the first time, hard ellipsoids and hard super-ellipsoids, in two, three and, for spheres, in higher dimensions. Together with the experimental research group of Paul Chaikin, we made some surprising discoveries about random packings of ellipsoids. Firstly, random packings of moderately aspherical ellipsoids are substantially denser that that of spheres, specifically, the density grows linearly with the aspect ratio, even though the packings were found to be hypostatic and not isostatic as commonly expected. An astounding packing fraction of 74% was found for a specific ellipsoid shape that we named ollipsoids (optimal ellipsoids). These results are detailed in the following publications:1. "Improving the Density of Jammed Disordered Packings using Ellipsoids" by A. Donev, I. Cisse, D. Sachs, E. A. Variano, F. H. Stillinger, R. Connelly, S. Torquato and P. M. Chaikin, Science, 303:990-993, 2004.
2. "Neighbor List Collision-Driven Molecular Dynamics Simulation for Nonspherical Particles. I. Algorithmic Details II. Applications to Ellipses and Ellipsoids", by A. Donev, F. H. Stillinger, and S. Torquato, J. Comp. Phys, 202(2):737-764 (part I) and 202(2):765-793 (part II), 2005, [physics/0110034].
4. "Experiments on Random Packings of Ellipsoids", W. Man, A. Donev , F. H. Stillinger, M. T. Sullivan, W. B. Russel, D. Heeger , S. Inati, S. Torquato and P. M. Chaikin, Phys. Rev. Lett., 94:198001, 2005.
At the time we discovered random packings of ellipsoids as dense as the FCC hard-sphere crystal, it was thought that the FCC crystal structure and maximal volume fraction of 74% applies to ellipsoids as well. However, using hard-ellipsoid molecular dynamics and some geometry we soon discovered that there are denser ellipsoid crystals, as dense as 77% in volume fraction:
1. "Unusually Dense Crystal Packings of Ellipsoids", by A. Donev, F. H. Stillinger, P. M. Chaikin and S. Torquato, Phys. Rev. Lett., 92:255506, 2004, [cond-mat/0110034].
Since then, this work has been extended to super-ellipsoids (generalized ellipsoids), which you can learn more about from the homepage of Dr. Salvatore Torquato.
Random Sphere Packings
We also performed detailed studies of large random packings of hard spheres in three and higher dimensions and found some surprising results, including that maximally random jammed packings of hard spheres are hyperinform (incompressible) and potentially exhibit long-ranged correlations, unlike hard-sphere fluids. Further details can be found in these papers:1. "Pair Correlation Function Characteristics of Nearly Jammed Disordered and Ordered Hard-Sphere Packings", by A. Donev, F. H. Stillinger, and S. Torquato, Phys. Rev. E, 71:011105, 2005, [cond-mat/0408550].
2. "Unexpected Density Fluctuations in Jammed Disordered Sphere Packings", by A. Donev, F. H. Stillinger, and S. Torquato, Phys. Rev. Lett., 95:090604, 2005, [cond-mat/0506406].
3. "Packing Hyperspheres in High-Dimensional Euclidean Spaces", by M. Skoge, A. Donev, F. H. Stillinger and S. Torquato, Phys. Rev. E, 74:041127, 2006 [ibid 75:029901, 2007], [cond-mat/0608362].
Glass Transition
One of the most fascinating open questions in condensed matter physics is the glass transition. Two central questions are whether there are thermodynamically-stable disordered (non-crystalline) solid phases and whether there is an ideal glass transition (vanishing configurational entropy in a disordered phase). By using our hard-sphere molecular dynamics algorithms we found convincing evidence that there can exist disordered solid phases and that there is no ideal glass transition in certain hard particle systems, as described in the following papers:1. "Do Binary Hard Disks Exhibit an Ideal Glass Transition?", by A. Donev, F. H. Stillinger, and S. Torquato, Phys. Rev. Lett., 96:225502, 2006, [cond-mat/0603183].
2. "Configurational Entropy of Binary Hard-Disk Glasses: Nonexistence of an Ideal Glass Transition", by A. Donev, F. H. Stillinger and S. Torquato, J. Chem. Phys., 127:124509, 2007.
3. "Calculating the Free Energy of Nearly Jammed Hard-Particle Packings Using Molecular Dynamics", by A. Donev, F. H. Stillinger, and S. Torquato, J. Comp. Phys., 225:509–527, 2007.
4. "Tetratic Order in the Phase Behavior of a Hard-Rectangle System", by A. Donev, J. Burton, F. H. Stillinger, and S. Torquato, Phys. Rev. B, Vol. 73:054109, 2006, [cond-mat/0508550].
These results point to a kinetic origin of the glass transition, and further study is needed to understand the geometrical origin of the configurational trapping experienced near the kinetic glass transition.
Multifunctional Composites
During my Ph.D. studies I also joined an effort in the group of Dr. Salvatore Torquato concerning the computational design of binary composites (mixtures of two materials) that optimize transport properties such as conductivity. This research led to the discovery that triply-periodic minimal surface structures are optimal for several transport properties, as illustrated in this figure for the Schwartz simple cubic surface bi-continuous structure:
 |
 |
Further details can be found in these papers and more recent publications by the Torquato group:
1. "Multifunctional Optimal Composite Microstructures: Simultaneous Transport of Heat and Electricity", by S.Torquato, S. Hyun and A. Donev, Phys. Rev. Lett., 89(26):266601, 2002.
2. "Manufacturable extremal low-dielectric, high-stiffness porous materials", S. Torquato, A. Donev, A. G. Evans, and C. J. Brinker, J. Appl. Phys., 97:124103, 2005.
3. "Minimal Surfaces and Multifunctionality", by S.Torquato and A. Donev, Proceedings of the Royal Society of London: Mathematical, Physical and Engineering Sciences, 460(2047):1849 - 1856, 2004.
4. "Optimal design of manufacturable three-dimensional composites with multifunctional characteristics", by S.Torquato, S. Hyun and A. Donev, J. Appl. Phys., 94(9):5748-5755, 2003.
Subsequent work in the group of Dr. Salvatore Torquato has also studied fluid permeability in such composite structures.